
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Полезные дефекты
|
|
При пластической деформации металлов (например, ковке, прокатке), генерируются многочисленные дислокации, по-разному ориентированные в пространстве, что затрудняет разрушение кристалла по сетке дислокаций. Таким образом увеличивается прочность металла, но в то же время снижается пластичность.
В искусственно выращенных рубинах, сапфирах для лазеров добавляют примеси (Cr, Fe, Ti) элементов — окрашивающие центры, которые участвуют в генерации когерентного света.
Дислокация — линейный дефект кристаллической решётки твёрдого тела, представляющий собой наличие " лишней" атомной полуплоскости.
Общее определение
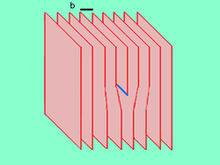
Основная геометрическая характеристика дислокаций — вектор Бюргерса. Если в идеальном кристалле провести замкнутый контур, а затем попытаться провести такой же контур вокруг области с дислокацией, то контур будет разорван. Вектор, который нужно провести для замыкания этого контура, и есть вектор Бюргерса дислокации. Он характеризует величину и направление сдвига атомных плоскостей, приводящего к образованию дислокации. В зависимости от угла φ между вектором Бюргерса и линией дислокации различают дислокации винтовые (φ =0), краевые (φ =90°) и смешанные (произвольный угол φ). Смешанные дислокации могут быть разложены на краевую и винтовую компоненты. Образование краевой дислокации можно представить как результат удаления из кристалла одной кристаллической полуплоскости. Линия, отделяющая дефектную область кристалла от бездефектной, называется линией дислокации. Простейшая наглядная модель краевой дислокации — книга, у которой от одной из внутренних страниц оторвана часть. Тогда, если страницы книги уподобить атомным плоскостям, то край оторванной части страницы моделирует линию дислокации.

Вопрос
ЭЛЕКТРОННЫЙ ГАЗ
- теоретич. модель, описывающая поведение электронов проводимости в электронных проводниках. В модели Э. г. пренебрегают кулоновским взаимодействием между электронами. Оправданием пренебрежения кулоновским взаимодействием (на качеств. уровне) служит, во-первых, существование ионов кри-сталлич. решётки, эл.-статич. заряд к-рых в среднем компенсирует заряд электронов, а, во-вторых, экранирование зарядов, существенно уменьшающее радиус действия кулоновских сил.
Электроны движутся в периодич. поле кристаллич. решётки. Поэтому состояние отд. электрона определяется его квазиимпульсом p и номером энергетич. зоны s (см. Зонная теория). Закон дисперсии (зависимость энергии  электрона в зоне s от квазиимпульса р)- сложная периодич. ф-ция. Э. г.- газ частиц со сложным законом дисперсии.
электрона в зоне s от квазиимпульса р)- сложная периодич. ф-ция. Э. г.- газ частиц со сложным законом дисперсии.
Как и свободные электроны, частицы Э. г. подчиняются Ферми - Дирака статистике. Э. г.- газ фермионов. Малое число электронов в полупроводниках (по сравнению с металлами) иногда позволяет для описания свойств Э. < г. в полупроводниках использовать Больцмана статистику.
Частицы Э. г. рассеиваются на фононах, друг на друге (межэлектронное рассеяние) и на любых нарушениях периодичности кристаллич. решётки (см. Рассеяние носителей заряда). Поэтому они имеют конечную длину свободного пробега l, конечное время жизни т = l/u, где u - тепловая скорость электрона. Чем лучше выполняются неравенства 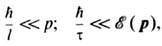 тем Э. г. ближе к идеальному газу.
тем Э. г. ближе к идеальному газу.
Модель Э. г. позволяет вычислить многие термодина-мич. и кинетич. характеристики электронных проводников. В нек-рых случаях (в полупроводниках) Э. г. может иметь темп-ру, отличную от темп-ры решётки (см. Горячие электроны). Под воздействием высокочастотных эл.-магн. полей Э. < г. металлов и полупроводников (особенно в постоянном магн. поле) ведёт себя как электронная или электронно-дырочная плазма (см. Плазма твёрдых тел); об Э. г. под действием сильного давления см. в ст. Экстремальное состояние вещества.
Исторически первым и простейшим вариантом модели Э. < г. была теория металлов Друде - Лоренца, в к-рой Э. < г. рассматривался как идеальный газ (см. Друде теория металлов). Теорию Друде - Лоренца сменила Зоммерфельда теория металлов, в к-рой учтено вырождение Э. г. Теория Э. < г. по Друде - Лоренцу сохраняет своё значение для полупроводников, если принять во внимание, что число частиц Э. г. зависит от темп-ры, а эффективная масса носителей заряда отлична от массы свободного электрона. Этим учитывается взаимодействие электронов с кристаллич. решёткой.
В электронной теории металлов наряду с моделью Э. г. используется модель электронной ферми-жидкости, когда необходимо и возможно учесть межэлектронное взаимодействие (см. Квантовая жидкость). Реально это удаётся осуществить вблизи основного состояния электронной системы. При kT< < 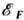 ,
, 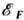 где - ферми-энергия, термодина-мич. ф-лы и многие ф-лы физ. кинетики не изменяются при переходе от модели Э. г. к модели электронной ферми-жидкости, если под
где - ферми-энергия, термодина-мич. ф-лы и многие ф-лы физ. кинетики не изменяются при переходе от модели Э. г. к модели электронной ферми-жидкости, если под 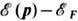 понимать энергию квазичастицы (её принято отсчитывать от энергии Ферми). Согласно теории ферми-жидкости, энергия квазичастицьг учитывает взаимодействие между электронами; заряд квазичастицы равен заряду свободного электрона; число квазичастиц равно числу частиц Э. г. В полупроводниках из-за малости числа частиц электронного газа взаимодействие между электронами несущественно.
понимать энергию квазичастицы (её принято отсчитывать от энергии Ферми). Согласно теории ферми-жидкости, энергия квазичастицьг учитывает взаимодействие между электронами; заряд квазичастицы равен заряду свободного электрона; число квазичастиц равно числу частиц Э. г. В полупроводниках из-за малости числа частиц электронного газа взаимодействие между электронами несущественно.
Теория Друде — классическое описание движения электронов в металлах. Эта теория была предложена немецким физиком Паулем Друде через 3 года после открытия электрона как частицы — в 1900 году. Она отличается простотой и наглядностью, хорошо поясняет эффект Холла, удельную проводимость в постоянном и переменном токе и теплопроводность в металлах и поэтому до сегодняшнего дня актуальна.