
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ознаки зображень на основі поділу інтенсивності
|
|
Екстракція розподілених ознак із фрагментів та сегментів інтенсивності зображення. Для отримання тривимірної поверхні зображення спочатку кольорове зображення перетворюється у відтінки сірого. Кожна елементарна клітинка, піксель, приймає значення від чорного до білого кольору, яке позначимо як b – яскравість. Діапазон всіх можливих значень яскравості знаходиться в межах 0÷ 255.
Для перетворення використовуємо алгоритм BT709 з наступними коефіцієнтами R, G, B:
R = 0, 2125; G = 0, 7154; B = 0, 0721 (1)
Значення яскравості пікселів обчислюється з рівняння відносного заповнення клітинки у відсотках від чорного кольору:
b = (256 – ci) × 100 / 256, (2)
або у відсотках від білого кольору:
b = ci × 100 / 256 (3)
де ci (i = 1, 2, 3) – значення компоненти R (G або B) сірого кольору пікселя.
Для гістограми зображення маємо
 (1)
(1)
а для кумулятивної гістограми:
 (2)
(2)
де  – загальна кількість пікселів зображення,
– загальна кількість пікселів зображення, 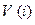 – частоти за інтенсивністю,
– частоти за інтенсивністю, 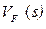 – накопичувальна частота для даної інтенсивності, n – кількість інтервалів кумулятивної гістограми, s, i – номер інтервалу (значення інтенсивності).
– накопичувальна частота для даної інтенсивності, n – кількість інтервалів кумулятивної гістограми, s, i – номер інтервалу (значення інтенсивності).
Поділимо простір інтенсивності зображення на n фрагментів горизонтальними площинами XOY з інтервалом (кроком фрагментації інтенсивності) d=255/n (рис.1). На рис.1а показано тестове зображення і його поверхню інтенсивності у тривимірному просторі, розділену на фрагменти (рис.1б).

a б
Рис.1. Тестове зображення (а), тривимірне представлення його інтенсивності (б).
До інтенсивності застосуємо такі поняття як фрагмент інтенсивності та сегмент інтенсивності. Фрагментів є 256. Кожен містить пікселі, інтенсивність яких дорівнює номеру фрагмента. Кількість фрагментів можна зменшити, якщо крок фрагментації вибрати більшим за одиницю, тобто 2, 3, 4 тощо. Тоді у фрагменті знаходяться пікселі, інтенсивність яких задовольняє умові
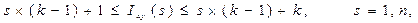 (5)
(5)
де k – крок фрагмента, s – номер фрагмента,  – інтенсивність пікселя фрагмента.
– інтенсивність пікселя фрагмента.
Сегмент – це послідовність фрагментів, починаючи від першого до заданого. Для кроку k = 1 сегментів є також 256: перший місить один перший фрагмент, другий – перший і другий фрагменти, третій – перший, другий і третій фрагменти і т.д. Останній сегмент – це повне зображення.
Розглянемо ряд ознак інтенсивності, які можна обчислити при врахуванні розбиття її на фрагменти чи сегменти. Назвемо ці ознаки розподіленими в зв’язку з їх залежністю від номеру фрагмента чи сегмента, а фактично від рівня інтенсивності, характерного для відповідної частини інтенсивності.
Фрагменти. Найпростішими ознаками інтенсивності зображення вважаємо математичне сподівання та середньоквадратичне відхилення значень кумулятивної гістограми (фрагментів) зображення:
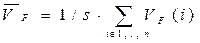 (6а)
(6а)
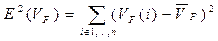 . (6б)
. (6б)
де  – математичне сподівання значень кумулятивної гістограми,
– математичне сподівання значень кумулятивної гістограми, 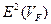 – середньоквадратичне відхилення.
– середньоквадратичне відхилення.
Для пікселів фрагмента визначаємо ознаки за їх координатами: математичне сподівання координат пікселів фрагмента
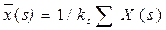 ,
,  ,
, 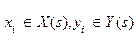 (7)
(7)
та дисперсію координат пікселів у фрагменті
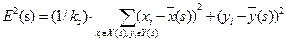 , (8)
, (8)
де  – кількість пікселів у фрагменті,
– кількість пікселів у фрагменті, 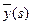 – математичне сподівання координат пікселів фрагмента, X(s), Y(s) – множини координат пікселів фрагмента,
– математичне сподівання координат пікселів фрагмента, X(s), Y(s) – множини координат пікселів фрагмента,  – дисперсія координат пікселів у фрагменті.
– дисперсія координат пікселів у фрагменті.
Розподіленими ознаками зображення, які враховують кооординати та інтенсивність, приймаємо:
· площинну густину пікселів фрагмента:
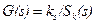 , (9)
, (9)
· або обернену величину – питому площу на один піксель:
 (10)
(10)
де 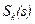 – площа фігури, що покриває пікселі фрагмента, визначена, як площа прямокутника або круга, що охоплюють точки пікселів, наприклад:
– площа фігури, що покриває пікселі фрагмента, визначена, як площа прямокутника або круга, що охоплюють точки пікселів, наприклад:
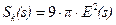 (11)
(11)
Також розглядаємо об’ємну густину пікселів фрагмента:
 (12)
(12)
або питомий об’єм на один піксель:
 . (13)
. (13)
У формулах (9-11) інтенсивність входить неявно – через кількість пікселів та номер фрагмента.
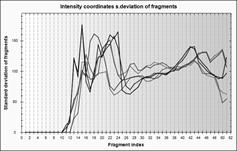
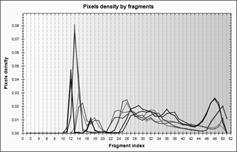
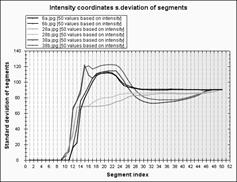
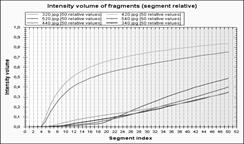
На рис.2 наведено три пари облич, для яких на графіках (рис.3) подані чотири розподілені характеристики від змінної s – номера фрагмента, а саме: відносного та абсолютного значень об’єму фрагмента, середньоквадратичного відхилення координат пікселів та густини пікселів у фрагменті. На перших двох графіках важко виділити пари облич і неможливо виділити вирази облич, на третьому графіками чітко виділяємо типи і вирази облич. На четвертому – вирази дещо зливаються в одному типі. Отже, для розпізнавання облич серед запропонованих ознак найкраще підходить функція середньоквадратичного відхилення координат пікселів від номера фрагмента.






а б в г д е
Рис. 2. Тестові зображення облич.
а б
облич.
а б
Рис. 2. Розподілені ознаки для зображень з рис.1: а – середньоквадратичне відхилення координат пікселів, б – густина пікселів
в г
Рис. 3. Розподілені ознаки для зображень з рис.2: а, б – об’єм сегментів, в – середньоквадратичне відхилення координат пікселів, г – густина пікселів.
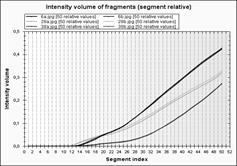
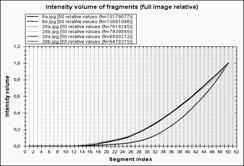
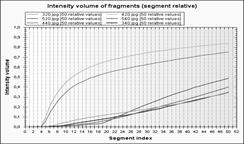
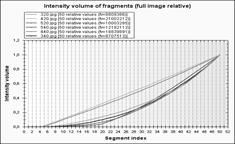
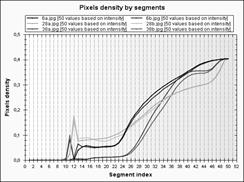
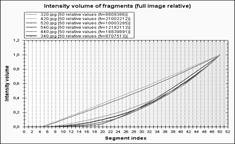
На рис.4-5 наведено приклади зображень з бібліотеки Ванга [15] та графіки аналогічних до рис.3 розподілених ознак. На основі представлених прикладів для пошуку образів приймаємо ознаку густину пікселів.






а б в г д е
Рис. 4. Тестові зображення з бібліотеки Ванга.
















а б
Ванга.


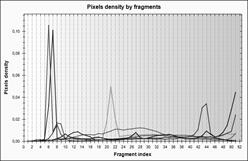
в г
.
Рис. 5. Сегментні ознаки для образів з рис.4: а, б – об’єм сегментів,
в – середньоквадратичне відхилення координат пікселів, г – густина пікселів.
Сегменти. При фрагментації інтенсивності обчислюємо об’єми сегментів. Сегмент інтенсивності формується об’єднанням фрагментів від першого до s-го рухом зверху вниз (рис.1б) і, відповідно, обчислюється його об’єм:
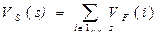 , (5)
, (5)
де 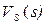 – об’єм s-го сегмента,
– об’єм s-го сегмента, 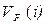 – об’єм i-го фрагмента, S, F –індекси для позначення сегмента та фрагмента.
– об’єм i-го фрагмента, S, F –індекси для позначення сегмента та фрагмента.
До розподілених ознак за інтенсивністю зображення відносимо математичне сподівання та середньоквадратичне відхилення значень об’єму сегментів зображення (останній n - ий сегмент – це повне зображення).
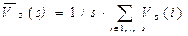 (6а)
(6а)
 . (6б)
. (6б)
де 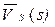 – математичне сподівання об’ємів s сегментів,
– математичне сподівання об’ємів s сегментів, 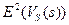 – середньоквадратичне відхилення об’єму сегментів (від першого до s-го).
– середньоквадратичне відхилення об’єму сегментів (від першого до s-го).
Для пікселів сегмента визначаємо ознаки за їх координатами: математичне сподівання координат пікселів сегмента:
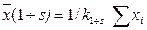 ,
, 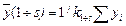 ,
, 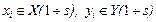 (6)
(6)
 , (7)
, (7)
де 1÷ s – інтервал фрагментів, що утворюють сегмент, 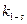 – кількість пікселів сегмента,
– кількість пікселів сегмента,  ,
, 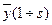 – математичне сподівання координат пікселів,
– математичне сподівання координат пікселів, 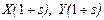 – множини координат пікселів сегмента,
– множини координат пікселів сегмента, 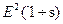 – дисперсія координат пікселів.
– дисперсія координат пікселів.
Для обчислень приймаємо універсальну фігуру – коло. Для визначення площі обчислюємо математичне сподівання координат пікселів сегмента та їх дисперсію:
Після обчислення площі за формулою:
 (8)
(8)
маємо ознаку густини пікселів у сегменті:
 . (9)
. (9)
де 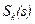 – площа фігури, що покриває пікселі сегмента, визначена, як площа прямокутника або круга, що охоплюють точки пік селів, наприклад:
– площа фігури, що покриває пікселі сегмента, визначена, як площа прямокутника або круга, що охоплюють точки пік селів, наприклад:
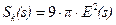 (11)
(11)
Також розглядаємо об’ємну густину пікселів сегмента:
 (12)
(12)
або питомий об’єм на один піксель:
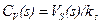 . (13)
. (13)
У формулах (9-11) інтенсивність входить неявно – через кількість пікселів та номер сегменту. Наведені формули (6-13) обчислюються також для фрагментів (формули та відповідні характеристики не подані).
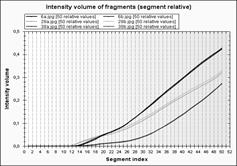
На рис.2 наведено три пари облич, для яких на графіках (рис.3) подані чотири розподілені характеристики від змінної s – номера сегмента (розмірності сегмента), а саме: відносного та абсолютного значень об’єму сегментів, середньоквадратичного відхилення координат пікселів та густини пікселів у сегменті. На перших двох графіках трудно виділити пари облич і неможливо виділити вирази облич, на третьому графіками чітко виділяємо типи і вирази облич. На четвертому – вирази дещо зливаються в одному типі. Отже, для розпізнавання облич серед запропонованих ознак найкраще підходить функція середньоквадратичного відхилення координат пікселів від номера сегмента.






а б в г д е
Рис. 2. Тестові зображення облич.











а б
в г
Рис. 3. Розподілені ознаки для зображень з рис.2: а, б – об’єм сегментів, в – середньоквадратичне відхилення координат пікселів, г – густина пікселів.
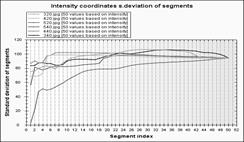
На рис.4-5 представлені приклади зображень з бібліотеки Ванга [15] та графіки аналогічних до рис.3 розподілених ознак. На основі представлених прикладів для пошуку образів приймаємо ознаку густину пікселів.






а б в г д е
Рис. 4. Тестові зображення з бібліотеки Ванга.
а б

в г
Рис. 5. Сегментні ознаки для образів з рис.4: а, б – об’єм сегментів,
в – дньоквадратичне відхилення координат пікселів, г – густина пікселів.
Ознаки відділеногосегменту. При відсіканні горизонтальною площиною частини інтенсивності отримуємо сегмент зображення (рис.2), в якому виділяємо дві частини: інформативну та порожню.

Рис.2. Тестове зображення
Порожню частину характеризуємо площею  та множиною
та множиною  вертикальних відрізків, що покривають простір забраної частини зображення RLi, (Bp(x, y)) – i-ий суцільний відрізок променя, що проходить під однією суцільною поверхнею яскравості на рівні Bp(x, y). Для відрізків RU = довжина - RL.
вертикальних відрізків, що покривають простір забраної частини зображення RLi, (Bp(x, y)) – i-ий суцільний відрізок променя, що проходить під однією суцільною поверхнею яскравості на рівні Bp(x, y). Для відрізків RU = довжина - RL.
Наявність ………… дозволяє для кожного значення яскравості 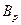 основного образу знайти площу перерізу його яскравості
основного образу знайти площу перерізу його яскравості
Таким чином, отримуємо ознаки основного образу: 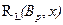 ,
, 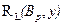 - сума довжин відрізків на висоті яскравості B з координатою x чи y або Bsp(
- сума довжин відрізків на висоті яскравості B з координатою x чи y або Bsp(  (Bp, x), Bsp(
(Bp, x), Bsp(  (Bp, y)) - значення яскравості пікселя знімка з тими ж координатами та площа поперечного перерізу горбів яскравості образу
(Bp, y)) - значення яскравості пікселя знімка з тими ж координатами та площа поперечного перерізу горбів яскравості образу
Відношення одиниці до зазначених площ та сум довжин відрізків слугують також як безрозмірні інваріантні до розмірів ознаки образу.
Кількості відрізків для бічного та фронтального знімків є різними, а площі поперечного перерізу яскравості для певного рівня 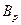 є однаковими для різних знімків.
є однаковими для різних знімків.
Близькою до яскравості є гістограма довжин суцільних відрізків під поверхнею яскравості:
K(RL)= {K(RL d1), K(RL d2), …, K(RL dM)},
де K(RL) - кількість всіх відрізків, K(Lo d 2) –кількість відрізків довжин у інтервалі;
або гістограма площ поперечного перерізу під поверхнею яскравості:
K(Bsp (RL))= {K(Bsp (RL d1)), K(Bsp (RL d2)), …, K(Bsp (RL dN))},
де K(Bsp (RL)) - кількість всіх суцільних площ поперечного перерізу, K(Bsp (RL d 2)) –кількість значень площ в конкретному інтервалі.
Для оцінки ступеня структуризації зображення на основі горизонтальних сегментів введемо ряд параметрів, якими характеризуємо зображення з точки зору його структурних властивостей, зокрема верхній індекс позначає рівень сегмента. Для цього використаємо об’єм простору інтенсивності:
1) структурні коефіцієнти ступеня трансформації інтенсивності образу між довільними i-им та j-им сегментами:
 (11)
(11)
де 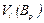 ,
,  – об’єми “пагорбів” сегмента;
– об’єми “пагорбів” сегмента;
2) структурні коефіцієнти ступеня трансформації інтенсивності образу в межах сегмента на основі площі перерізу
 , (12)
, (12)
де 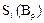 ,
,  – площа кінцевого і початкового рівнів інтенсивності сегмента (найвищого і найнижчого).
– площа кінцевого і початкового рівнів інтенсивності сегмента (найвищого і найнижчого).
3) структурні коефіцієнти ступеня трансформації між довільними i-им та j-им сегментами:
 = MSi (S (Bp)) / MSj (S (Bp)). (13)
= MSi (S (Bp)) / MSj (S (Bp)). (13)
Для сегментів: 1- площц і інтенсивності!!!!!!!!!!!!!
1) Середня площа поперечного перерізу у сегменті:
MS (S (Bp)) = (1 / K(S (Bp)) 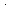 ∑ S i(Bp)) (9)
∑ S i(Bp)) (9)
2) Середнє квадратичне відхилення площі поперечного перерізу у сегменті:
де K(S (Bp)) – кількість рівнів яскравості у горизонтальному сегменті.