
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Лабораторная работа
|
|
Исходные данные:
Объем выпуска продукции ОАО «Камаз-Металлургия» за 2000-2012 годы:
| Год | Объем выпуска | Литье чугунное | Литье стальное | Литье цветное | Поковки |
| 418370, 9 | 146795, 9 | ||||
| 422236, 8 | 161061, 1 | 69353, 88 | 47961, 9 | ||
| 430681, 8 | 164282, 3 | 145298, 6 | 70740, 96 | 50359, 995 | |
| 453883, 1 | 167567, 9 | 161281, 4 | 72155, 78 | 52877, 9948 | |
| 479062, 5 | 170919, 3 | 179022, 4 | 73598, 89 | 55521, 8945 | |
| 493147, 8 | 174337, 7 | 198714, 8 | 53856, 2377 | ||
| 498049, 9 | 165620, 8 | 220573, 5 | 59615, 1 | 52240, 5505 | |
| 456253, 7 | 149058, 7 | 196310, 4 | 60211, 25 | 50673, 334 | |
| 417564, 1 | 150549, 3 | 157048, 3 | 60813, 37 | 49153, 134 | |
| 412785, 7 | 173131, 7 | 125638, 7 | 61421, 5 | 52593, 8534 | |
| 417923, 5 | 199101, 4 | 100510, 9 | 62035, 71 | 56275, 4231 | |
| 472450, 5 | 228966, 7 | 120613, 1 | 62656, 07 | 60214, 7027 | |
| 532146, 9 | 263311, 7 | 144735, 7 | 63282, 63 | 60816, 8497 |
Используемый инструментарий: пакет Statistica 6.0.
Решение:
Назначим суммарный объем выпуска независимой переменной У, литье чугунное, литье стальное, литье цветное, поковки соответственно зависимыми переменными Х1, Х2, Х3, Х4.
Распределение переменных. Сначала изучим распределение зависимых переменных от объема выпуска.

Гистограмма независимой переменной У.
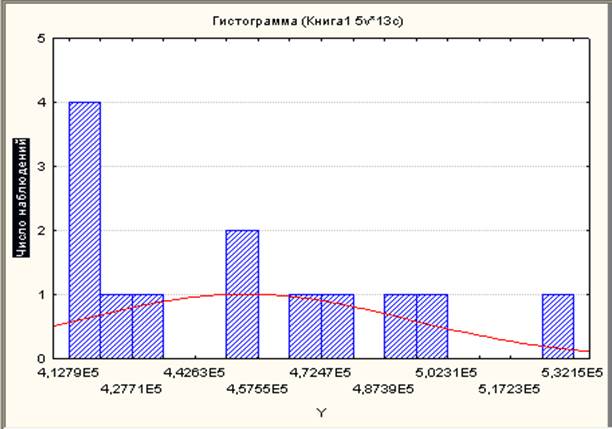
Распределение существенно отличается от нормального. Коэффициенты корреляции могут оказаться существенно завышенными или заниженными при наличии в выборке существенных выбросов.
Распределение переменной У (диаграмма размаха).
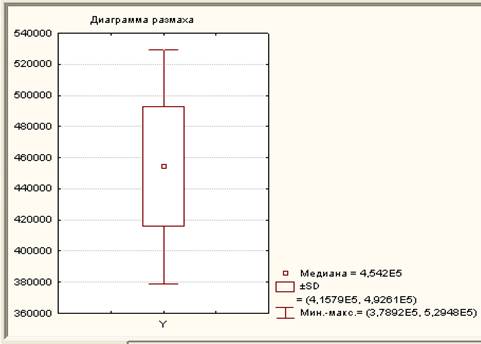
Корреляции между переменными:

Результаты множественной регрессии.
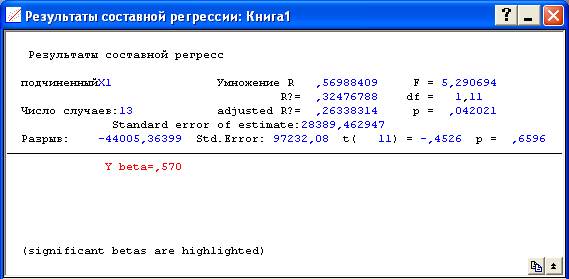
Регрессионные коэффициенты. Чтобы узнать, какие из независимых переменных дают больший вклад в предсказание предиктора, изучим регрессионные (или B) коэффициенты.
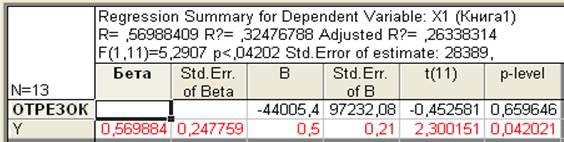
Частные корреляции. Частные корреляции являются корреляциями между соответствующей независимой переменной и зависимой переменной, скорректированными относительно других переменных. Таким образом, это корреляция между остатками после корректировки относительно независимых переменных. Частная корреляция представляет самостоятельный вклад соответствующей независимой переменной в предсказание зависимой переменной.


Критерий Фишера, суммарные стандартные ошибки.
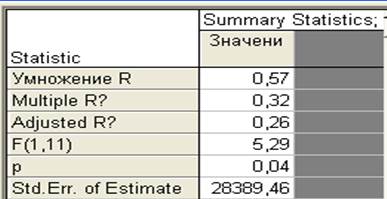
Получастные корреляция являются корреляциями между соответствующей независимой переменной, скорректированной относительно других переменных, и исходной (нескорректированной) зависимой переменной. Таким образом, получастная корреляция является корреляцией соответствующей независимой переменной после корректировки относительно других переменных, и нескорректированными исходными значениями зависимой переменной. Иначе говоря, квадрат получастной корреляции является показателем процента Общей дисперсии, самостоятельно объясняемой соответствующей независимой переменной, в то время как квадрат частной корреляции является показателем процента остаточной дисперсии, учитываемой после корректировки зависимой переменной относительно независимых переменных. Здесь получастная и частная корреляция имеют равные значения.
Построчный анализ остатков.
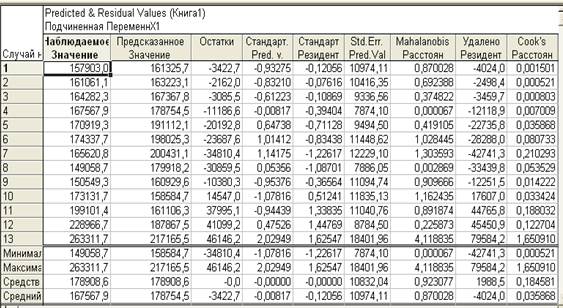
Построчный график остатков. 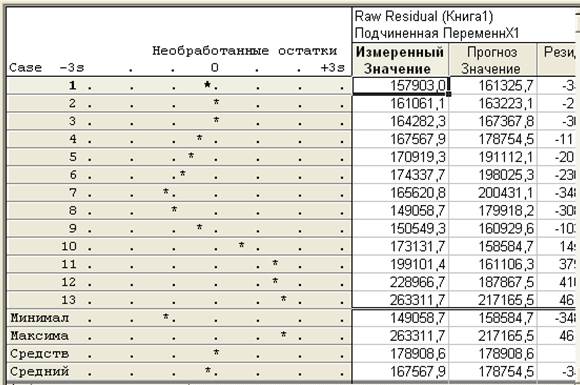
Масштаб, используемый в построчном графике в самой левой колонке, задается в терминах сигмы, т.е. стандартного отклонения остатков. Если один или несколько наблюдений попадают за границы ± 3 * сигма, то, вероятно, следует исключить соответствующие наблюдения (это легко достигается с помощью условий отбора) и выполнить анализ снова, чтобы убедиться в отсутствии смещения ключевых результатов, вызванного этими выбросами в данных.
Удаленные остатки. Другой очень важной статистикой, позволяющей оценить масштаб проблемы выбросов, являются удаленные остатки. Они определяются как стандартизованные остатки для соответствующих наблюдений, которые получились бы при исключении соответствующих наблюдений из анализа.

Как было замечено ранее, множественная линейная регрессия предполагает линейную связь между переменными в уравнении, и нормальным распределением остатков. Если эти предположения нарушаются, окончательные заключения могут оказаться неточными. Нормальный вероятностный график остатков наглядно показывает наличие или отсутствие больших отклонений от высказанных предположений.
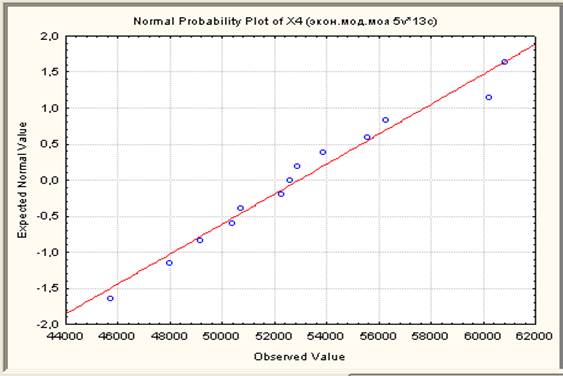
Этот график строится следующим образом. Сначала остатки регрессии ранжируются. Для этих упорядоченных остатков вычисляются z-значения (т.е. стандартные значения нормального распределения), исходя из предположения, что данные имеют нормальное распределение. Эти z-значения откладываются по оси Y на графике. Если наблюдаемые остатки (отложенные по оси X) нормально распределены, то все значения будут располагаться на графике вблизи прямой линии; на данном графике все точки лежат очень близко к прямой линии. Если остатки не распределены нормально, то они будут отклоняться от линии. На этом графике также могут стать заметны выбросы.
|