Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методичні матеріали
|
|
ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД
КИЇВСЬКИЙ НАЦІОНАЛЬНИЙ ЕКОНОМІЧНИЙ УНІВЕРСИТЕТ
імені Вадима Гетьмана”
Факультет інформаційних систем і технологій
Кафедра економіко-математичного моделювання
“ЗАТВЕРДЖУЮ”
Проректор з навчальної роботи
______________________А.М. Колот
“______” ________________ 2010 р.
Методичні матеріали
щодо змісту та організації самостійної роботи студентів, поточного і підсумкового контролю їх знань з дисципліни
“ОПТИМІЗАЦІЙНІ МЕТОДИ ТА МОДЕЛІ”
(для бакалаврів всіх спеціальностей)
Укладачі: к.ф.-м.н., доц. Великоіваненко Г.І., к.е.н., доц. Савіна С.С.
Декан факультету О.Д. Шарапов
“______”______________ 2010 р.
Завідувач кафедри
економіко-математичних
методів В.В. Вітлінський
“______”______________ 2010 р.
1. Перелік питань, що охоплюють зміст робочої програми дисципліни.
1. Принципи моделювання соціально-економічних систем і процесів.
2. Сутність економіко-математичної моделі.
3. Необхідність використання математичного моделювання економічних процесів.
4. Етапи математичного моделювання.
5. Сутність адекватності економіко-математичних моделей.
6. Проблеми оцінювання адекватності моделі.
7. Способи перевірки адекватності економіко-математичних моделей.
8. Поняття адаптації та адаптивних систем.
9. Сутність оптимізаційних моделей. Приклади економічних задач математичного програмування.
10. Загальна постановка задачі лінійного програмування. Приклади економічних задач лінійного програмування.
11. Модель задачі лінійного програмування в розгорнутому і скороченому вигляді, а також в матричній і векторній формах.
12. Властивості розв’язків задачі лінійного програмування. Геометрична інтерпретація задач лінійного програмування.
13. Означення планів задачі лінійного програмування (допустимий, опорний, оптимальний).
14. Побудова опорного плану задачі лінійного програмування, перехід до іншого опорного плану.
15. Теорема про оптимальність розв’язку задачі лінійного програмування симплекс-методом.
16. Знаходженння розв’язку задачі лінійного програмування. Алгоритм симплексного методу.
17. Симплексний метод із штучним базисом. Ознака оптимальності плану із штучним базисом.
18. Двоїста задача. Правила побудови двоїстої задачі. Симетричні й несиметричні двоїсті задачі.
19. Економічний зміст двоїстої задачі й двоїстих оцінок.
20. Теореми двоїстості, їх економічна інтерпретація.
21. Застосування теорем двоїстості в розв’язуванні задач лінійного програмування.
22. Аналіз розв’язків лінійних економіко-математичних моделей. Оцінка рентабельності продукції. Доцільність введення нової продукції.
23. Аналіз обмежень дефіцитних і недефіцитних ресурсів.
24. Аналіз коефіцієнтів цільової функції задач лінійного програмування.
25. Цілочислове програмування. Область застосування цілочислових задач в плануванні й управлінні виробництвом.
26. Геометрична інтерпретація задачі цілочислового програмування.
27. Метод Гоморі.
28. Постановка задачі нелінійного програмування, математична модель. Геометрична інтерпретація.
29. Графічний метод розв’язування задач нелінійного програмування.
30. Метод множників Лагранжа. Теорема Лагранжа. Алгоритм розв’язування задачі на безумовний екстремум.
31. Поняття про опуклі функції. Геометрична інтерпретація задачі опуклого програмування на площині.
32. Сідлова точка та необхідні і достатні умови її існування. Теорема Куна-Таккера.
33. Квадратична функція та її властивості.
34. Постановка задачі квадратичного програмування та її математична модель.
35. Градієнтні методи розв’язання задач нелінійного програмування та їх класифікація.
36. Метод Франка-Вульфа. Алгоритм розв’язування задачі нелінійного програмування.
37. Математична постановка задачі динамічного програмування, її економічний зміст. Принцип оптимальності Беллмана.
38. Основні рекурентні співвідношення розв’язування задач динамічного програмування.
39. Методи розв’язування задач динамічного програмування. Основні кроки алгоритму розв’язування задачі динамічного програмування.
40. Основні поняття теорії ігор. Гра двох гравців з нульовою сумою, правила гри, ціна гри, пара оптимальних стратегій для двох осіб.
41. Платіжна матриця. Основна теорема теорії ігор. Принцип мінімаксу.
42. Гра в чистих стратегіях. Поняття сідлової точки і її знаходження.
43. Гра 2х2 в змішаних стратегіях. Алгоритм розв’язування задачі.
44. Зведення гри двох осіб до задачі лінійного програмування.
2. Приклади типових завдань, ЩО ВИНОСЯТЬСЯ НА ІСПИТ
1. Розв’язати задачі лінійного програмування графічним методом:
а) Z = x1 - 2x2 (min) б) Z = x1 + 3x2 (max)
x1 - x2 £ 1, x1 - x2 £ 1,
x1 + x2 ³ 2, 2x1 + x2 £ 2,
x1 - 2x2 £ 0, x1 - x2 ³ 0,
x1³ 0; x2 ³ 0. x1³ 0; x2 ³ 0.
в) Z = 3x1 + 2x2 (min) г) Z = x1 + x2 (max)
3x1 + 2x2 ³ 6, x1 + 2x2 £ 10,
x1 + 4x2 ³ 4, x1 + 2x2 ³ 2,
x1³ 0; x2 ³ 0. 2x1 + x2 £ 10,
x1³ 0; x2 ³ 0.
д) Z = 2x1 + 4x2 (max) є) Z = 2x1 + 4x2 (min)
3x1 + 2x2 £ 11, 3x1 + 2x2 £ 11,
-2x1 + x2 £ 2, -2x1 + x2 £ 2,
-x1 + 3x2 ³ 0, x1 - 3x2 £ 0,
x1³ 0; x2 ³ 0. x1³ 0; x2 ³ 0.
2. На виготовлення двох видів продукції (П1 і П2) витрачаються три види ресурсів 
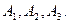 Наявність ресурсів дорівнює відповідно: 361, 520, 248. Витрати ресурсів на одиницю продукції П1 становлять відповідно: 13, 7, 17; на одиницю продукції П2 - 16, 4, 9. Ціна за одиницю продукції дорівнює відповідно: 11, 8. Побудувати модель лінійного програмування початкової й двоїстої задач. Знайти такий план виробництва, який би забезпечував найбільшу виручку. Дати економічне тлумачення розв’язків задач.
Наявність ресурсів дорівнює відповідно: 361, 520, 248. Витрати ресурсів на одиницю продукції П1 становлять відповідно: 13, 7, 17; на одиницю продукції П2 - 16, 4, 9. Ціна за одиницю продукції дорівнює відповідно: 11, 8. Побудувати модель лінійного програмування початкової й двоїстої задач. Знайти такий план виробництва, який би забезпечував найбільшу виручку. Дати економічне тлумачення розв’язків задач.
3. Знайти розв’язок наступних задач лінійного програмування шляхом графічного розв’язування двоїстої задачі й застосування теорем двоїстості:
а) 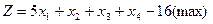
|
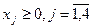 .
.
б) 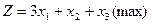
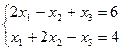
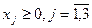 .
.
4. Для плану 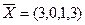 визначити, чи він є оптимальним для наступних задач (застосовуючи теореми двоїстості й не розв’язуючи задачі симплексним методом):
визначити, чи він є оптимальним для наступних задач (застосовуючи теореми двоїстості й не розв’язуючи задачі симплексним методом):
а) 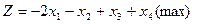
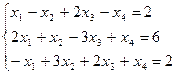
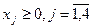
б) 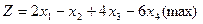
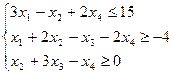
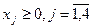
5. У наведених далі задачах:
а) побудуйте економіко-математичні моделі початкової й двоїстої задач;
б) приведіть задачі до канонічного виду й дайте економічне тлумачення основних й допоміжних змінних двох задач;
в) з наведеної останньої симплексної таблиці початкової задачі запишіть оптимальні плани 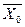 і
і 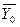 ;
;
г) визначте дефіцитні й недефіцитні ресурси, рентабельну та збиткову продукцію;
д) знайдіть межі зміни обсягів дефіцитних ресурсів, в котрих оцінка ресурсу залишається сталою (аналіз двоїстих оцінок на стійкість);
е) знайдіть межі зміни обсягів недефіцитних ресурсів;
є) знайдіть межі зміни цін на рентабельну і нерентабельну продукцію, в котрих структура оптимального плану початкової задачі не змінюється;
ж) в якому випадку розширення асортименту випуску за рахунок введення нової продукції буде доцільним, чи недоцільним?
5.1. Підприємство виготовляє три види продукції А, В і С, використовуючи для цього три види ресурсів I, II, III. Норми витрат усіх ресурсів на одиницю продукції та запаси ресурсів наведено в табл.1
Таблиця 1
| І II III |
Відома ціна одиниці продукції кожного виду: А - 9 ум.од., В -10 ум. од. і С - 16 ум.од. Визначити план виробництва продукції, що забезпечує підприємству найбільший доход.
Остання симплекс-таблиця даної задачімає такий вигляд (табл.2)
Таблиця 2
| Базис | Сб | А0 | ||||||
| X1 | X2 | X3 | X4 | X5 | X6 | |||
| X2 X3 X6 | 1/4 5/4 | 1/9 -1/18 –1/6 | -1/6 5/24 -1/8 | |||||
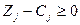
| 2/9 | 5/3 |
5.2. Підприємство виготовляє продукцію видів А, В і С, для чого використовує три види ресурсів І, II, III. Норми витрат усіх ресурсів на одиницю кожної продукції та обсяги ресурсів на підприємстві наведено в табл.1.
Таблиця 1
| Вид ресурсу | Норма витрат на одиницю продукції за видами | Запас ресурсу | ||
| А | В | С | ||
| І II III |
Відома ціна одиниці продукції кожного виду: А - 10 ум.од., В -14 ум.од. і С - 12 ум.од. Визначити план виробництва продукції, що забезпечує підприємству найбільший доход.
Остання симплекс-таблиця, що містить оптимальний план задачі, має такий вигляд (табл.2)
Таблиця 2
| Базис | Сб | А0 | ||||||
| X1 | X2 | X3 | X4 | X5 | X6 | |||
| X2 X5 X3 | 19/8 23/8 -3/4 | 5/8 1/8 -1/4 | -1/8 -5/8 1/4 | |||||
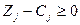
| 57/4 | 23/4 | 5/4 |
6. На основі умовно-оптимального плану цілочисельної задачі побудувати допоміжне обмеження Гоморі, приєднати його до умовно-оптимального плану, показаного у наведений нижче таблиці, і знайти цілі значення змінних задачі лінійного програмування.
а)
| І | Базис | Сб | А0 | -4 | ||||
| А1 | А2 | А3 | А4 | А5 | ||||
| Х1 | -4 | 7/2 | -5/2 | 5/2 | -3/2 | |||
| Х3 | 5/2 | 1/2 | 31/2 | 11/2 | ||||
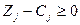
| -9 |
б)
| І | Базис | Сб | А0 | -1 | ||||
| А1 | А2 | А3 | А4 | А5 | ||||
| Х1 | 14/3 | -2/3 | 5/3 | 1/3 | ||||
| Х3 | 11/3 | 1/3 | 7/3 | |||||
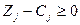
| 47/3 | 4/3 | 14/3 | 11/3 |
7. Розв’язати наступну задачу: компанія контролює три фабрики А1, А2, А3, здатні виготовляти 150, 60 та 80 тис.од. продукції щотижня. Компанія уклала договір з чотирма замовниками В1, В2, В3, В4, яким потрібно щотижня відповідно 110, 40, 60 та 80 тис.од. продукції. Вартість виробництва та транспортування 1000 од. продукції замовниками з кожної фабрики наведено в таблиці.
| Фабрика | Вартість виробництва і транспортування 1000 од. продукції за замовниками | |||
| В1 | В2 | В3 | В4 | |
| А1 | ||||
| А2 | ||||
| А3 |
Визначити для кожної фабрики оптимальний план перевезення продукції до замовників, що мінімізує загальну вартість виробництва і транспортних послуг.
8. Розв’язати графічним методом задачу нелінійного програмування; знайти глобальний екстремум:
а) 
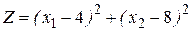
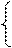
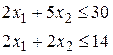
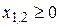 .
.
б) 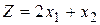
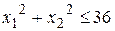 ,
,
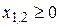 .
.
9. Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму наступної задачі нелінійного програмування:
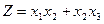


10. Користуючись теоремою Куна-Таккера, скласти функцію Лагранжа та записати необхідні і достатні умови існування сідлової точки наступної задачі нелінійного програмування:
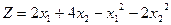
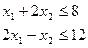
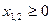
11. Розв’язати градієнтним методом наступну задачу нелінійного програмування, почавши процес з точки 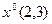 :
:
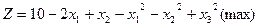
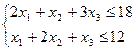
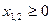
12. Розв’язати графічним методом наступну задачу дробово-лінійного програмування:

за умов
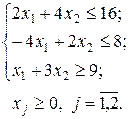
13. Фірма спеціалізується на виробництві офісних меблів, зокрема випускає дві моделі збірних книжкових полиць: А та В. Полиці обох моделей обробляють на двох верстатах: шліфувальному та полірувальному. Тривалість обробки у хвилинах однієї полиці кожної моделі відома:
| Тип верстату | Тривалість обробки однієї полиці, хв. | |
| А | В | |
| Шліфувальний | ||
| Полірувальний |
Час роботи обох верстатів обмежений і становить: для шліфувального 600 хв., для полірувального – 900 хв. на тиждень.
Вивчення ринку збуту показало, що тижневий попит на книжкові полиці обох типів не перевищує 20 одиниць.
Прибуток фірми від реалізації однієї полиці моделі А становить 300 грн., а моделі В – 400 грн.
Визначити обсяги виробництва книжкових полиць різних моделей, що максимізують прибуток фірми.
Необхідно: 1) розв’язати задачу графічним методом; 2) визначити двоїсту оцінку для ресурсу – час роботи шліфувального верстату.
14. В приведеній нижче таблиці (табл.1) містяться величини можливого збільшення продукції чотирьох нафтопереробних заводів при здійсненні додаткових капіталовкладень на їх реконструкцію та модернізацію.
Таблиця 1
| Капіталовкладення тис. грн | Збільшення виробництва 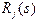 продукції, млн. грн.
заводи продукції, млн. грн.
заводи
| |||
| s | ||||
У таблиці 2 рамкою виділені умовні оптимальні розв’язки усіх кроків розв’язування наведеної динамічної задачі. Запишіть одержаний план інвестування заводів. На скільки він збільшує виробництво продукції?
Таблиця 2
| j =4 | j =3 | j =2 | j =1 | |||||
| s | 
| 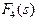
| 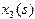
| 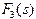
| 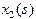
| 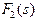
| 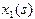
| 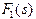
|
| 50, 100 | ||||||||
15. Дві конкуруючі фірми (гравці) реалізують на ринку продукцію, котра швидко псується. Кожний з гравців прагне зайняти по два сегмента ринку (має дві стратегії). Відомі прибуток (виграш) або збиток (програш) для кожного гравця і кожного сегмента ринку, які наведені в платіжній матриці С. Розв’язати гру, знайти пару оптимальних стратегій і ціну гри.
а) С = 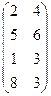 ; б) С =
; б) С = 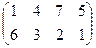
в)С = 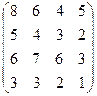 ;
;  г)
г)