
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Особливості поточного контролю знань студентів заочної Форми навчання
|
|
Поточний контроль здійснюється у таких формах:
1. Контроль систематичності та активності роботи на практичних, семінарських та лабораторних заняттях.
Усне опитування та перевірка на практичних заняттях знань згідно з тематикою практичних занять; а також матеріалу, винесеного на самостійне вивчення. Рівень знань, продемонстрований у відповідях і виступах на практичних заняттях, активність при обговоренні питань, що винесені на практичні заняття оцінюються від 0 до 5 балів.
2. Виконання контрольних завдань.
Виконання письмової контрольної роботи. Білет для контрольної роботи містить чотири завдання. Перелік теоретичних питань та практичних завдань, що виносяться на контрольну роботу див. п. 9.1 та п. 9.2. Оцінюються результати контрольної роботи від 0 до 10 балів.
3. Контроль виконання завдань для самостійного опрацювання.
Вибіркові види СРС. Студент обирає один з видів запропонованих вибіркових завдань для самостійного опрацювання (див. карту самостійної роботи студента п.2.1-2.2).Результати обраного завдання оцінюються від 0 до 5 балів.
Завдання поточного контролю оцінюються в діапазоні від 0 до 20 балів.
Підсумковий контроль знань студентів здійснюється у формі іспиту.
Іспит проводиться у письмовій формі за потоковою системою. Кожен студент отримує білет, що містить 10 завдань. Завдання білету охоплюють усі теми дисципліни “Оптимізаційні методи та моделі” згідно затвердженій навчальній програмі. Кожне завдання білету оцінюється за шкалою: 10; 8; 6; 0 балів, а саме:
10 балів ставиться, якщо відповідь студента є теоретично правильною, обґрунтованою, вичерпною, матеріал викладено в логічній послідовності та у повному обсязі, всі розрахунки правильні;
8 балів ставиться, якщо відповідь в основному правильна, студент володіє матеріалом, але допущені незначні помилки у формулюванні термінів, категорій, у розрахунках тощо;
6 балів ставиться, якщо відповідь правильна, але недостатньо обґрунтована; допущені суттєві помилки;
0 балів ставиться, якщо відповідь неправильна або відсутня, чи допущені грубі помилки, які свідчать про те, що студент не володіє відповідним матеріалом.
Результати іспиту оцінюються в діапазоні від 0 до 100 балів.
В разі, коли відповіді студента оцінені менше ніж в 30 балів, він отримує незадовільну оцінку за результатами іспиту (тобто 0 балів).
Загальна підсумкова оцінка з дисципліни складається з суми балів за результати поточного контролю знань та за виконання завдань, що виносяться на іспит (за умови, що на іспиті студент набрав не менше 30 балів), але не більше 100 балів.
Якщо на іспиті студент набрав менше 30 балів, а отже отримав незадовільну оцінку, загальна підсумкова оцінка включає лише результати поточного контролю.
Переведення даних 100-бальної шкали оцінювання в 4-х бальну шкалу та шкалу за системою ECTS здійснюється в такому порядку:
| Оцінка за бальною шкалою, що використовується в КНЕУ | Оцінка за національною шкалою | Оцінка за шкалою ECTS |
| 90-100 | відмінно | А |
| 80-89 | добре | B |
| 70-79 | C | |
| 66-69 | задовільно | D |
| 60-65 | E | |
| 21-59 | незадовільно з можливістю повторного складання | FX |
| 0-20 | незадовільно з обов’язковим повторним вивченням дисципліни | F |
6. Зразок екзаменаційного білету.
Зразок екзаменаційного білету для денної та вечірньої форм навчання
Білет №_____
1. Економічна постановка та математична модель задачі лінійного програмування (на прикладі задачі визначення оптимального плану виробництва).
2. Правила побудови двоїстих задач.
3. Основні поняття теорії ігор.
4. Фірма спеціалізується на виробництві офісних меблів, зокрема випускає дві моделі збірних книжкових полиць: А та В. Полиці обох моделей обробляють на двох верстатах: шліфувальному та полірувальному. Тривалість обробки у хвилинах однієї полиці кожної моделі відома:
| Тип верстату | Тривалість обробки однієї полиці, хв. | |
| А | В | |
| Шліфувальний | ||
| Полірувальний |
Час роботи обох верстатів обмежений і становить: для шліфувального 600 хв., для полірувального – 900 хв. на тиждень.
Вивчення ринку збуту показало, що тижневий попит на книжкові полиці обох типів не перевищує 20 одиниць.
Прибуток фірми від реалізації однієї полиці моделі А становить 300 грн., а моделі В – 400 грн.
Визначити обсяги виробництва книжкових полиць різних моделей, що максимізують прибуток фірми.
Необхідно: 1) записати математичну модель задачі; 2) знайти оптимальний план.
5. Для завдання 4 необхідно вказати яким чином зміниться прибуток, якщо: 1) буде збільшено на 1 хв. час роботи шліфувального верстату; 2)буде збільшено на 1 хв. час роботи полірувального верстату.
6. Дві конкуруючі фірми (гравці) реалізують на ринку продукцію, котра швидко псується. Кожний з гравців прагне зайняти по два сегмента ринку (має дві стратегії). Відомі прибуток (виграш) або збиток (програш) для кожного гравця і кожного сегмента ринку, які наведені в платіжній матриці С. Розв’язати гру, знайти пару оптимальних стратегій і ціну гри.
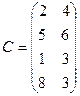
Зразок екзаменаційного білету для заочної форми навчання
Білет №_____
1. Етапи математичного моделювання.
2. Економічна постановка та математична модель задачі лінійного програмування (на прикладі задачі визначення оптимального плану виробництва).
3. Правила побудови двоїстих задач.
4. Економічний зміст двоїстої задачі й двоїстих оцінок.
5. Геометрична інтерпретація задачі цілочислового програмування.
6. Метод множників Лагранжа.
7. Основні поняття теорії ігор.
8. Фірма спеціалізується на виробництві офісних меблів, зокрема випускає дві моделі збірних книжкових полиць: А та В. Полиці обох моделей обробляють на двох верстатах: шліфувальному та полірувальному. Тривалість обробки у хвилинах однієї полиці кожної моделі відома:
| Тип верстату | Тривалість обробки однієї полиці, хв. | |
| А | В | |
| Шліфувальний | ||
| Полірувальний |
Час роботи обох верстатів обмежений і становить: для шліфувального 600 хв., для полірувального – 900 хв. на тиждень.
Вивчення ринку збуту показало, що тижневий попит на книжкові полиці обох типів не перевищує 20 одиниць.
Прибуток фірми від реалізації однієї полиці моделі А становить 300 грн., а моделі В – 400 грн.
Визначити обсяги виробництва книжкових полиць різних моделей, що максимізують прибуток фірми.
Необхідно: 1) записати математичну модель задачі; 2) знайти оптимальний план.
9. Для завдання 8 необхідно вказати яким чином зміниться прибуток, якщо: 1) буде збільшено на 1 хв. час роботи шліфувального верстату; 2)буде збільшено на 1 хв. час роботи полірувального верстату.
10. Дві конкуруючі фірми (гравці) реалізують на ринку продукцію, котра швидко псується. Кожний з гравців прагне зайняти по два сегмента ринку (має дві стратегії). Відомі прибуток (виграш) або збиток (програш) для кожного гравця і кожного сегмента ринку, які наведені в платіжній матриці С. Розв’язати гру, знайти пару оптимальних стратегій і ціну гри.
Рекомендована література
Основна:
1. Вітлінський В. В., Наконечний С.І., Шарапов О.Д. та ін. Економіко-математичне моделювання: Навчальний посібник/ За заг.ред. В.В.Вітлінського. – К.: КНЕУ, 2008. – 536 с.
2. Вітлінський В. В. Моделювання економіки: Навч. посібник. – К.: КНЕУ, 2002.
3. Наконечний С.І., Савіна С.С. Математичне програмування: Навч.посіб. – К.: КНЕУ, 2003. – 452 с.
Додаткова:
1. Абчук В.А. Экономико-математические методы, С-П, “Союз”, 1999.
2. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высшая школа, 1986. – 317 c.
3. Вітлінський В.В., Наконечний С.І., Терещенко Т.О. Математичне програмування: Навч.-метод.посібник для самост.вивч.дисц. – К.: КНЕУ, 2001. – 248 с.
4. Горчаков А.А., Орлова И.В. Компьютерные экономико-математические модели, М.: “ЮНИТИ”, 1995.
5. Економічний ризик: ігрові моделі: Навч. посібник / В.В. Вітлінський, П.І. Верченко, А.В. Сігал, Я.С. Наконечний; За ред. В.В. Вітлінського. – К.: КНЕУ, 2002. – 446 с.
6. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М.: ДИС, 1997. – 365 c.
7. Збірник задач з курсу “Математичне програмування”. Ч.2. /Укл.: С.І.Наконечний, В.В.Вітлінський та інш. – К.: КНЕУ, 1998. – 224 с.
8. Исследование операций в экономике (Под ред. Кремера). – М.: Банки и биржи, ЮНИТИ, 1997. – 407 с.
9. Колемаев В.А. Математическая экономика. – М.: ЮНИТИ, 1998. – 240 с.
10. Мазаракі А.А., Толбатов Ю.А. Математичне програмування в Excel: Навч. посіб. – К.: Четверта хвиля, 1998. – 208 с.
11. Хазанова Л.Э. Математическое моделирование в экономике, М, “БЕК”, 1998.
12. Эддоус М., Стенсфилд Р. Методы принятия решений. М., Аудит, 1997.
13. Ястремский А.И. Стохастические модели математической экономики. – К., 1983.