
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Cryptanalytic Methods for Modern Ciphers.
|
|
Block ciphers like DES are intended to be very hard to break, and they are largely successful in achieving this. Having even copious quantities of corresponding plaintext and ciphertext, it is intended that the fastest way to discover the key, so as to be able to decrypt other messages, would be a brute-force search, that is, trying every possible key until the right one is found.
Many block ciphers appear to meet this condition. Two cryptanalytic methods that can do slightly better with some of the earlier block ciphers, such as DES and LUCIFER, are differential cryptanalysis and linear cryptanalysis.
Differential Cryptanalysis. However, if one is fortunate enough to have a large quantity of corresponding plaintext and ciphertext blocks for a particular unknown key, a technique called differential cryptanalysis, developed by Eli Biham and Adi Shamir, is available to obtain clues about some bits of the key, thereby shortening an exhaustive search.
After two rounds of DES, knowing both the input and output, it is trivial to determine the two subkeys used, since the outputs of both f-functions are known. For each S-box, there are four possible inputs to produce the known output. Since each subkey is 48 bits long, but the key is only 56 bits long, finding which of the four possibilities is true for each group of six bits in the subkeys is a bit like solving a crossword puzzle.
As the number of rounds increases, though, the simple correlations disappear. Differential cryptanalysis represents an approach to finding more subtle correlations.
In fact, however, a complete pattern of which bits change and do not change in the input and in the output is the subject of differential cryptanalysis. The basic principle of differential cryptanalysis, in its classic form, is this: the cipher being attacked has a characteristic if there exists a constant X such that given many pairs of plaintexts A, B, such that B = A xor X, if a certain statement is true about the key, E(B, k) = E(A, k) xor Y for some constant Y will be true with a probability somewhat above that given by random chance.
Linear Cryptanalysis. Linear cryptanalysis, invented by Mitsuru Matsui, is a different, but related technique. Instead of looking for isolated points at which a block cipher behaves like something simpler, it involves trying to create a simpler approximation to the block cipher as a whole.
For a great many plaintext-ciphertext pairs, the key that would produce that pair from the simplified cipher is found, and key bits which tend to be favored are likely to have the value of the corresponding bit of the key for the real cipher. The principle is a bit like the summation of many one-dimensional scans to produce a two-dimensional slice through an object in computer-assisted tomography.
Truncated differentials. It is of course possible that some of the bits of E(A, k) xor E(B, k) will be more likely to match those of Y than others. If one can, in addition, ignore some of the bits of A and B, one has a truncated differential for the cipher being attacked, and this technique, due to Lars R. Knudsen, has been found to be very powerful.
Higher-order Differentials. Another important addition to the available techniques deriving from differential cryptanalysis is the use of higher-order differentials, which first appeared in a paper by Xuejia Lai.
A differential characteristic of the type described above, where for a large number of different values of A, B equals A xor X, and the encrypted versions of A and B for a given key, k, are expected to have the relation E(A, k) = E(B, k) xor Y, if a target statement about the key k is true, can be made analogous to a derivative in calculus, and then it is termed that Y is the first derivative of the cipher E at the point X.
A second-order derivative would then be one involving a second quantity, W, such that E(A, k) xor E(B, k) = E(C, k) xor E(D, k) xor Z is expected to be true more often than would be true due to chance, where not only is B = A xor X, but C = A xor W and D = B xor W. In that case, Z is the second derivative of the cipher E at the point X, W. Since xor performs the function of addition and subtraction, the four items encrypted for any A are just lumped together in this case, but if differential cryptanalysis were being performed over another field where the distinction is significant, then Y=E(A+X, k)-E(A, k) and Z=(E(A+X+W, k)-E(A+W, k))-(E(A+X, k)-E(A, k)) would be the appropriate equations to use.
The Boomerang Attack. Recently, a means of improving the flexibility of differential cryptanalysis was discovered by David A. Wagner. Called the boomerang attack, it allows the use of two unrelated characteristics for attacking two halves of a block cipher.
This diagram shows how the attack might work if everything goes perfectly for a particular initial block.
1. Start with a random block of plaintext. Based on the characteristic known for the first half of the cipher, if we XOR a certain vector with it, called d1 (equal to 00100000 in the diagram), the result after half-enciphering the two plaintext blocks, before and after the XOR, will differ by c1 (equal to 00110110 in the diagram), if what we wish to learn about the key happens to be true.
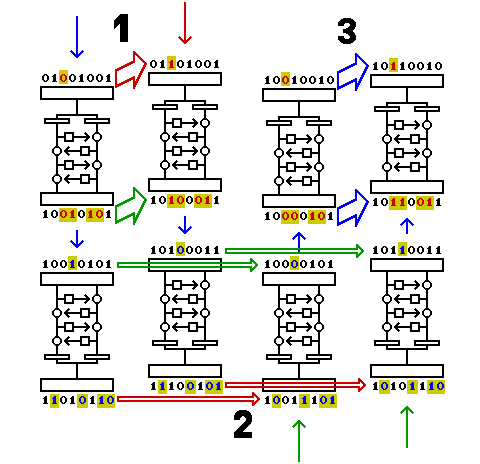
2. Since the characteristic applies only to the first half of the cipher, the results after the whole block cipher won't be related. Take those two results and XOR each one with d2 (equal to 01001011 in the diagram), which is the vector corresponding to the characteristic for the second half of the cipher. In each case, XORing d2 with a ciphertext block is expected to change the result after deciphering halfway by c2 (equal to 00010000 in the diagram), again, if something is true of the key.
3. With two intermediate results that differ by c1, if each one has c2 XORed to it, the two results of the XOR will still differ by c1. Since this difference now relates to the first half characteristic, it can be seen in the final output, thus indicating the truth or otherwise of two hypotheses about the key.
This increases the potential effectiveness of differential cryptanalysis, because one can make use of characteristics that do not propagate through the complete cipher.