Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример. .
|
|
§ 16. Уравнение плоскости в пространстве.
10. Различные виды уравнения на плоскости.
Принципы построения уравнения плоскости в пространстве во многом совпадают с построением прямой на плоскости. Это связано с тем, что размерность прямой отличается от??? плоскости на единицу. Размерность плоскости отличается на единицу от??? пространства. Поэтому плоскость определяется двумя линейно-независимыми векторами и точкой, через которую эта плоскость проходит.
Утверждение 1. Пусть в плоскости 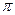 задана т.
задана т. 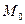 и два неколлинеарных вектора
и два неколлинеарных вектора  и
и  . Тогда т.
. Тогда т.  . (1)
. (1)
Доказательство.
|Þ Пусть т. М лежит в плоскости, тогда это означает, что 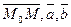 компланарны Þ в силу неколлинеарности
компланарны Þ в силу неколлинеарности  и
и  , вектор
, вектор 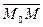 может быть представлен как линейная комбинация
может быть представлен как линейная комбинация  и
и  , т.е. справедливо (1).
, т.е. справедливо (1).
Ü | если справедливо (1), то 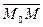 компланарен с
компланарен с  и
и  Þ
Þ 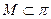 , ч.т.д.∎
, ч.т.д.∎
Уравнение (1) будет называться уравнением плоскости в векторной форме. Оно означает лишь, что плоскость проходит через т. 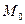 и параллельно
и параллельно  и
и  . Зафиксируем в пространстве аффинновую систему координат. Пусть
. Зафиксируем в пространстве аффинновую систему координат. Пусть  и
и  - радиус-вектора т.
- радиус-вектора т. 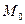 и М.
и М.
Тогда (1) перепишем: 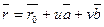 - векторное уравнение плоскости. (2)
- векторное уравнение плоскости. (2)
Если теперь зафиксировать координаты векторов  ,
,  ,
,  ,
,  , например
, например  , то уравнение (2):
, то уравнение (2):  (3)
(3)
Уравнение (3) называется параметрическим уравнением плоскости. Если его переписать в виде: 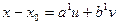
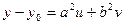
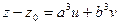 ,
,
Представляет собой линейную зависимость столбцов матрицы: 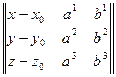 = 0 (4)
= 0 (4)
Разлагая этот определитель по первому столбцу получим:
 (5)
(5)
где  (6)
(6)
Уравнение (4) является уравнением плоскости, проходящей через т.  и параллельно
и параллельно  .
.
Если в плоскости заданы 3 точки  ,
,  , то в качестве векторов
, то в качестве векторов  и
и  :
: 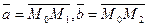 .
.
Уравнение плоскости, проходящей через 3 точки: 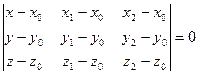 (7)
(7)
Если в уравнение (5) раскрыть скобки и обозначить 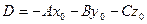 , то
, то  - общее уравнение плоскости (8)
- общее уравнение плоскости (8)
Отметим, что в силу неколлинеарности 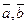 хотя бы один из определителей (6) отличен от нуля Þ уравнением первой степени.
хотя бы один из определителей (6) отличен от нуля Þ уравнением первой степени.
Таким образом, показали, что любое уравнение плоскости может быть записано в виде уравнение первой степени.
Докажем и обратное: любое уравнение первой степени вида (8) представляет собой уравнение некоторой плоскости.
Пусть в (8) 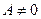 , тогда (8) имеет частное решение:
, тогда (8) имеет частное решение: 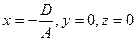 , которое определяет координаты точки, через которую проходит плоскость. А вектора имеют значения
, которое определяет координаты точки, через которую проходит плоскость. А вектора имеют значения 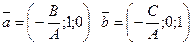 .
.
Покажем, что плоскости, проходящие через полученную точку параллельно  и
и  определяются уравнением (8). Действительно, уравнение плоскости имеет вид:
определяются уравнением (8). Действительно, уравнение плоскости имеет вид:
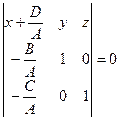 , где
, где  эквивалентно (8)
эквивалентно (8)
доказана теорема 1: Пусть в пространстве- в точности поверность первого порядка.
20. Взаимное расположение плоскостей в пространстве. Полупространства.
Утверждение 1. Вектор  параллелен плоскости
параллелен плоскости 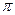 , заданной уравнением (8)
, заданной уравнением (8) 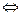
 (9)
(9)
Доказательство. Для доказательства утверждения необходимо и достаточно показать, что, если  отложить от некоторой точки плоскости, то конец также будет лежать на плоскости.
отложить от некоторой точки плоскости, то конец также будет лежать на плоскости.
Пусть 
 ,
, 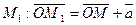 ,
, 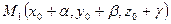 , проверим, что
, проверим, что 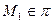 . Подставляя в уравнение (8):
. Подставляя в уравнение (8): 
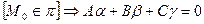 , ч.т.д.∎
, ч.т.д.∎
Утверждение 2. Плоскости 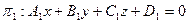 (10)
(10)
 (11)
(11)
параллельны  (12)
(12)
Доказательство.
Ü | Плоскости параллельны, если вектор параллельный одной плоскости, будет параллелен другой. Поэтому, если выполняется условие (12), то в силу утверждения 1 плоскости параллельны.
|Þ пусть  , тогда вектора
, тогда вектора  , которые параллельны плоскости
, которые параллельны плоскости  , должны быть параллельны
, должны быть параллельны  Þ в силу утверждения 1 выполняется:
Þ в силу утверждения 1 выполняется:
 , ч.т.д.∎
, ч.т.д.∎
Утверждение 3. Плоскости  и
и  , заданные уравнениями (10, 11), совпадают
, заданные уравнениями (10, 11), совпадают 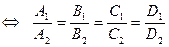 (13)
(13)
Доказательство.
Ü | очевидно
|Þ пусть плоскости совпадают, тогда первые два равенства следуют из утверждения 2 и доказываем третье равенство.
Пусть т 
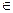 обеим плоскостям, тогда
обеим плоскостям, тогда 
В силу соотношения (12) получим:  .
.
Умножим первое уравнение последней системы на 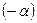 и прибавим ко второму:
и прибавим ко второму:  мы доказали уравнение (13), ч.т.д.∎
мы доказали уравнение (13), ч.т.д.∎
Утверждение 4. Плоскости  и
и  , заданные уравнениями (10, 11), параллельны и не совпадают Û
, заданные уравнениями (10, 11), параллельны и не совпадают Û  (14)
(14)
Утверждение 5. Плоскости  и
и  , заданные уравнениями (10, 11), пересекаются Û
, заданные уравнениями (10, 11), пересекаются Û  - неколлинеарны.
- неколлинеарны.
Утверждение 6. Пусть плоскости  и
и  , заданные уравнениями (10, 11), пересекаются на прямой l, тогда плоскость
, заданные уравнениями (10, 11), пересекаются на прямой l, тогда плоскость  проходит через эту прямую Û её уравнение имеет вид:
проходит через эту прямую Û её уравнение имеет вид:
 , (15)
, (15)
где  одновременно.
одновременно.
Доказательство. Аналогично для пучка прямых, так как (15) – это уравнение пучка плоскостей, проходящих через l.
30. Плоскость в пространстве с прямоугольной декартовой системой координат.
Пусть в пространстве задана прямоугольная декартова система координат 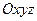 . Пусть плоскость
. Пусть плоскость 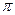 проходит через т.
проходит через т.  и
и 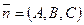 - некоторый вектор
- некоторый вектор 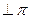 , тогда
, тогда  .
.
Условие перпендикулярности двух векторов в ортогональном базисе:

В ортогональном базисе коэффициенты А, В, С общего уравнения (8) можно??? как коэффициенты векторной нормали.
Вектор нормали используется для решения задач нахождения угла между плоскостями, угла между прямой и плоскостью и т.д.
По аналогии с прямой на плоскости строится нормальное уравнение плоскости.

Пусть в пространстве с прямоугольной декартовой системой координат задана плоскость 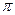 . Проведем из начала координат ось
. Проведем из начала координат ось  .
.
Пусть т. N – это точка пересечения прямой l с плоскостью 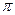 ,
, 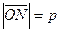
Тогда произвольная т. М пространства  Û
Û 
Другими словами,  , (16)
, (16)
|
 - единичный вектор, являющийся масштабным вектором оси l.
- единичный вектор, являющийся масштабным вектором оси l.
|
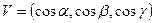 , где
, где  - углы с осями
- углы с осями 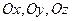 .
.
Получаем нормальное уравнение плоскости:  .
. 
§ 17. Уравнение прямой в пространстве.
10. Уравнение прямой в произвольной аффиновой системе координат.
В предыдущем § было указано, что если две плоскости пересекаются, то они пересекаются по прямой. Поэтому в произвольной аффиновой системе координат уравнение прямой в следующем виде:
 (1)
(1)
Плоскости  и
и  не параллельны. Условие не параллельности плоскостей
не параллельны. Условие не параллельности плоскостей  и
и  равносильно:
равносильно: 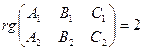 (2)
(2)
Тогда система (1) при условии (2) представляет систему линейно независимых уравнений, совместную и имеет общее решение следующего вида:  , (3)
, (3)
где  - частные решения (1),
- частные решения (1),  - ФСР соответствующей системы линейно ОУ.
- ФСР соответствующей системы линейно ОУ.
Геометрически (3) означает, что т. 
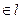 , тогда " т.
, тогда " т.  получается прибавлением к радиус-вектору т.
получается прибавлением к радиус-вектору т. 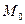 некоторого коллинеарного вектора,
некоторого коллинеарного вектора, 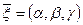
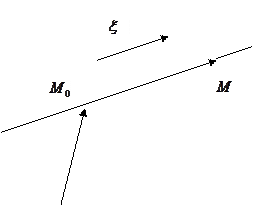 Таким образом,
Таким образом,  , по аналогии с прямыми на плоскости, является направляющим вектором прямой. Система уравнений (1), удовлетворяющая условию (2) называется общим уравнением прямой в пространстве. Уравнение (3) называется векторно-параметрическим уравнением прямой в пространстве.
, по аналогии с прямыми на плоскости, является направляющим вектором прямой. Система уравнений (1), удовлетворяющая условию (2) называется общим уравнением прямой в пространстве. Уравнение (3) называется векторно-параметрическим уравнением прямой в пространстве.

Можно переписать в виде:  , (3’)
, (3’)
где 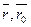 - радиус-вектор т.
- радиус-вектор т. 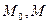 ,
,  - направляющий вектор.
- направляющий вектор.
Перепишем уравнение (3):  (4)
(4)
- параметрическое уравнение прямой в пространстве.
Если исключить из (4) параметр t получим: 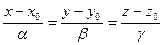 (5)
(5)
- каноническое уравнение прямой в пространстве, (5) – пропорция.
Пример. 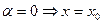 , значит прямая лежит в плоскости
, значит прямая лежит в плоскости 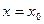 .
.
Если 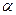 и
и 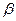 равны нулю, то прямая лежит в плоскостях
равны нулю, то прямая лежит в плоскостях 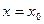 и
и  , что означает есть линия пересечения плоскостей – прямая параллельная оси
, что означает есть линия пересечения плоскостей – прямая параллельная оси  .
.
Если необходимо написать уравнение прямой, проходящей через две точки  и
и  .
.
 - направляющий вектор
- направляющий вектор
 (6)
(6)
- уравнение прямой, проходящей через две точки.
Каждая прямая может быть представлена как линия пересечения двух плоскостей.
Уравнение прямой (5) также можно рассматривать как пересечение двух плоскостей, каждая из которых определяет плоскость параллельную одной из координатных осей.
Утверждение 1. Если прямая l задана как пересечение двух плоскостей системой (1), то вектор 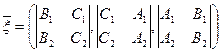 (7)
(7)
Является направляющим вектором l.
Доказательство.
Отметим, что в силу условия (2) вектор  , определенный по формуле (7) должен быть равен 2. Определитель следующего вида
, определенный по формуле (7) должен быть равен 2. Определитель следующего вида 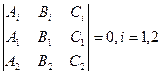 , разложим по 1ой строке:
, разложим по 1ой строке:
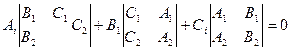 , в силу утверждения 1 из предыдущего параграфа, означает, что
, в силу утверждения 1 из предыдущего параграфа, означает, что  параллелен плоскостям
параллелен плоскостям  и
и  .
.
Þ  параллелен и их пересечению Þ значит является направляющим вектором, ч.т.д.∎
параллелен и их пересечению Þ значит является направляющим вектором, ч.т.д.∎
Замечание. Если прямоугольная декартова система координат, то 
Являются векторами нормали для плоскостей  и
и  .
.
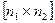 - направляющий вектор искомой прямой, а его координаты вычисляются по формулам (7).
- направляющий вектор искомой прямой, а его координаты вычисляются по формулам (7).
20. Взаимное расположение двух прямых в пространстве.
Будем рассматривать прямые 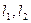 , заданные каноническими уравнениями:
, заданные каноническими уравнениями:
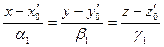 (8)
(8)
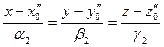 (9)
(9)
Прямые 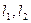 либо пересекаются, либо параллельны (в частном случае совпадают), либо скрещиваются.
либо пересекаются, либо параллельны (в частном случае совпадают), либо скрещиваются.
Для изучения взаимного расположения прямых вводят 3 основных вектора:
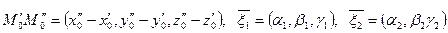
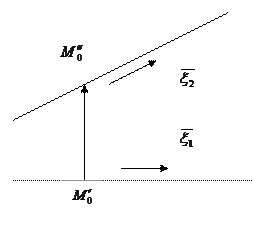

В случае параллельных или пересекающихся прямых существует плоскость, которой эти прямые принадлежат. Поэтому выполняется условие:  (10)
(10)
Þ если прямые скрещиваются, то условие (10) не выполняется, т.е. справедливо
Утверждение 2. Прямые 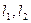 скрещиваются Û
скрещиваются Û 
 .
.
Если прямые пересекаются, то может решаться задача нахождения угла между прямыми. В этом случае угол определяется углом между направляющими векторами.
|
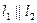 , то возникает задача нахождения расстояния между ними:
, то возникает задача нахождения расстояния между ними: 

Рис.7.
Плоскость, содержащая параллельные прямые имеет вектор нормали  .
.
Чтобы построить перпендикуляр строим плоскость  , содержащие эти прямые и плоскость
, содержащие эти прямые и плоскость  ,
,
Если прямые пересекаются, то плоскость, содержащая эти прямые в качестве вектора нормали имеет 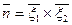 .
.
Если две прямые скрещиваются, то  .
.
Кроме того, чтобы построить вектор нормали этих плоскостей, найдем 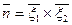 . Расстояние между этими плоскостями равно расстоянию между скрещенными прямыми. Другой способ нахождения расстояния между скрещенными прямыми: найти высоту параллепипеда, построенного на векторах
. Расстояние между этими плоскостями равно расстоянию между скрещенными прямыми. Другой способ нахождения расстояния между скрещенными прямыми: найти высоту параллепипеда, построенного на векторах 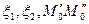 если в качестве основания брать параллелограмм, построенный на векторах
если в качестве основания брать параллелограмм, построенный на векторах  :
:  .
.
ПРАКТИЧЕСКАЯ ЧАСТЬ.
СМ. ПРИЛОЖЕНИЯ