Свойства проекции.

1⁰. Проекция вектора на ось равна произведению длины вектора 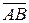на косинус угла между вектором и осью:

.

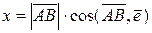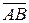Рис.8. - проекция вектора на ось L.а) , б)

Действительно, пусть .

Если (см. рис. 8а), то , поэтому

.

Если (см. рис. 8б), то , и

.

2⁰. При умножении вектора на число его проекция на ось также умножается на это число: .

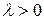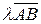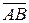Действительно, если , то угол между векторами и равен углу между и , т.е. l и .

Если , то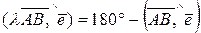

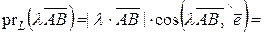
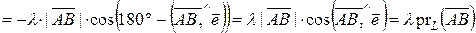
3⁰. Проекция суммы векторов на ось равна сумме проекций слагаемых:

.

Справедливость этого утверждения следует из рис.9. В случае а) , б)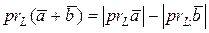

а) б)

Рис.9. Иллюстрация доказательства свойства о проекции суммы векторов.

Следствие. Свойство (3) справедливо для " количества векторов.

4⁰.Скалярное произведение векторов.

Определение 1. Скалярным произведением двух векторов и называется число, равное произведению длин этих векторов на косинус угла между ними.

Т.о., если , – вектора, то скалярное произведение обозначается, и .