Свойства изоморфных пространств.

1. Нулевому элементу V соответствует нулевой элемент и наоборот.

Доказательство: Если .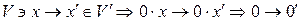

2. Если элементам 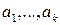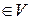соответствуют , то линейная комбинация векторов 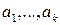равна нулю V, т.е. линейная комбинация с теми же коэффициентами 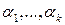равна нулю, т.е. .

Доказательство следует из 1.

3. Если V и изоморфны, то максимальное число линейно независимых векторов в каждом из пространств одно и тоже, т.е. два изоморфных пространства имеют одну и туже размерность.

4. Пространства разных размерностей не могут быть изоморфными.

Теорема 6. Любые два 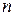–мерных линейных пространства V и над одним и тем же полем изоморфны.

Доказательство. Выберем в V базис ­­­− базис 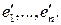Каждому элементу 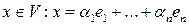, поставим в соответствие элемент с теми же координатами 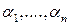в базисе .

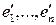Однако это соответствие взаимнооднозначно, т.к. 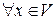имеет единственным образом определенные координаты 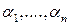, которые в свою очередь, определяют единственный элемент .

В силу равноправности V и , соответствует единственный 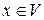. Легко видеть, что если в силу введенного соответствия.

Таким образомо все линейные пространства данной размерности 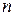–ная полем изоморфны, то есть их свойства, связанные с линейными операциями неразличимы.

Тема 5. Пространство геометрических векторов,