
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема 3. Система линейных уравнений.
|
|
1о. Определения, обозначения.
Определение 1. Системой 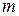 линейных уравнений с
линейных уравнений с 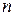 неизвестными
неизвестными  над полем
над полем  называется система выражений вида
называется система выражений вида
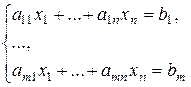 (1)
(1)
где 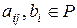 . Элементы
. Элементы 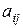 называются коэффициентами системы (1),
называются коэффициентами системы (1),  – ее свободные члены. Если все
– ее свободные члены. Если все 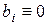 , то система (1) называется однородной, иначе – неоднородной.
, то система (1) называется однородной, иначе – неоднородной.
Определение 2. Совокупность 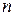 элементов поля
элементов поля  :
: 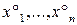 называется решением (1), если после подстановки их вместо
называется решением (1), если после подстановки их вместо 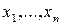 соответственно во все уравнения (1) получаются тождества.
соответственно во все уравнения (1) получаются тождества.
Определение 3. Если система (1) имеет хотя бы одно решение, то она называется совместной, если решений нет – несовместной.
Пример. 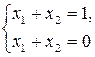 – несовместная.
– несовместная.  – совместная.
– совместная.
Определение 4. Два решения 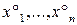 и
и  являются различными, если нарушается одно из равенств
являются различными, если нарушается одно из равенств  , …,
, …, 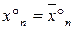 .
.
Определение 5. Если система (1) имеет единственное решение, то она называется определенной, если у системы существует по крайней мере два различных решения, то система называется неопределенной.
Пример. 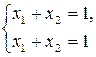 – неопределенная система.
– неопределенная система.
Решить систему линейных уравнений – это значит выяснить, совместна она или нет, и в случае совместности найти все ее решения.
Определение 6. Две системы линейных уравнений (СЛУ) с одинаковым числом неизвестных и над одинаковым полем называются эквивалентными, если они имеют одно и то же множество решений.
СЛУ удобно записывать с помощью матрицы:
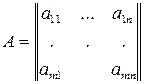 ,
, 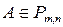 .
.
Матрица 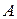 называется основной матрицей системы (1) или матрицей системы (1).
называется основной матрицей системы (1) или матрицей системы (1).
Если ввести
 ,
,  ,
,
то систему (1) можно переписать в матричном виде
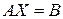 (2)
(2)
Наряду с основной матрицей 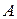 удобно рассматривать расширенную матрицу системы (1):
удобно рассматривать расширенную матрицу системы (1):
 ,
, 
2о. Формулы Крамера.
Рассмотрим частный случай, когда  и
и 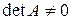 , т.е.
, т.е. 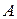 – невырожденная матрица.
– невырожденная матрица.
Теорема 1. (правило Крамера) Система 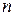 уравнений с
уравнений с 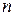 неизвестными в случае, когда
неизвестными в случае, когда  , имеет решение, причем только одно. Это решение находится по формулам:
, имеет решение, причем только одно. Это решение находится по формулам:
 ,
,  , (3)
, (3)
где 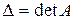 ,
, 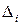 – определитель матрицы, получаемой из
– определитель матрицы, получаемой из 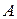 заменой
заменой 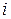 -ого столбца на столбец свободных членов, т.е.
-ого столбца на столбец свободных членов, т.е.
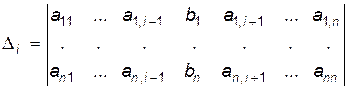 .
.
Формулы (3) называются формулами Крамера.
Доказательство. Запишем систему в матричном виде (2):
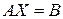 ,
,
т.к. 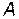 – квадратная матрица и
– квадратная матрица и 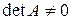
 определена обратная матрица
определена обратная матрица
 .
.
Тогда умножая (2) слева на 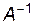 , имеем:
, имеем:
 , т.е.
, т.е.
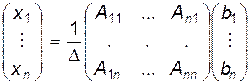

 .
.
Здесь 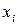 определяется через алгебраические дополнения к элементам
определяется через алгебраические дополнения к элементам 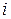 -ого столбца матрицы
-ого столбца матрицы 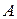 , умноженными на элементы столбца
, умноженными на элементы столбца  . Видно, что это можно переписать в виде формул (3).
. Видно, что это можно переписать в виде формул (3).
Покажем, что это решение единственно. Пусть 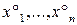 – решение (1), т.е.
– решение (1), т.е.

Умножим первое уравнение на 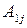 , второе – на
, второе – на  , …, и сложим (здесь
, …, и сложим (здесь 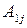 , …,
, …, 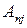 – алгебраические дополнения к элементам
– алгебраические дополнения к элементам 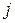 -ого столбца матрицы
-ого столбца матрицы 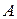 ). Имеем:
). Имеем:
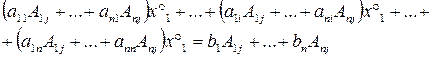
Здесь коэффициенты при 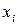 есть сумма произведений элементов
есть сумма произведений элементов 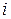 -ого столбца матрицы
-ого столбца матрицы 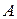 на алгебраические дополнения к элементам
на алгебраические дополнения к элементам 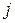 -ого столбца
-ого столбца 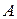 . По теоремам о разложении по «своему» и «чужому» столбцу имеем, что коэффициент при
. По теоремам о разложении по «своему» и «чужому» столбцу имеем, что коэффициент при  равен
равен  , а остальные – нули, т.е.
, а остальные – нули, т.е.


 , т.е. те же формулы.
, т.е. те же формулы.
Т.о., (3) дают единственное решение.