
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример. Замечание. Если рассматривать однородную СЛУ с
|
|
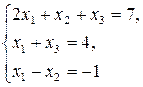 .
. 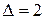 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 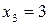 .
.
Замечание. Если рассматривать однородную СЛУ с 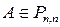 и
и 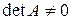 , то формулы Крамера дают единственное нулевое решение.
, то формулы Крамера дают единственное нулевое решение.
Следствие. Если однородная система 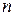 линейных уравнений с
линейных уравнений с 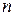 неизвестными имеет ненулевое решение, то
неизвестными имеет ненулевое решение, то  .
.
3о. Условие совместности СЛУ.
Теорема 2. (теорема Кронекерра–Капелли). Для того, чтобы система (1) была совместной, необходимо и достаточно, чтобы ранг ее расширенной матрицы был равен рангу основной матрицы, т.е.
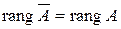 .
.
Доказательство. Очевидно, что 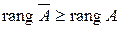 .
.
Для доказательства перепишем систему (1) в виде:
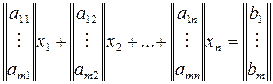 (4)
(4)
где выделены столбцы матрицы  , являющиеся элементами
, являющиеся элементами 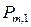 .
.
Необходимость. Если существует решение, то запись (4) означает, что столбец свободных членов есть линейная комбинация столбцов матрицы. Значит, добавление этого столбца не изменяет числа линейно независимых столбцов.
Достаточность. Пусть 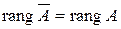 . В этом случае базисный минор матрицы
. В этом случае базисный минор матрицы 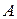 является базисным и для
является базисным и для  . Это и означает, что столбец свободных членов есть линейная комбинация тех столбцов матрицы
. Это и означает, что столбец свободных членов есть линейная комбинация тех столбцов матрицы 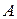 , в которых расположен базисный минор, а значит, и всех столбцов матрицы
, в которых расположен базисный минор, а значит, и всех столбцов матрицы 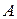 (остальные можно взять с коэффициентом 0). Очевидно, что коэффициенты этой линейной комбинации и являются решениями системы (1), т.е. есть хотя бы одно решение.
(остальные можно взять с коэффициентом 0). Очевидно, что коэффициенты этой линейной комбинации и являются решениями системы (1), т.е. есть хотя бы одно решение.
4о. Построение решений СЛУ.
Теорема Кронекера–Капелли устанавливает совместимость СЛУ, но не дает практического рецепта их нахождения. Ниже дается один из возможных способов.
Пусть рассматривается произвольная система 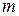 уравнений с
уравнений с 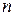 неизвестными и пусть
неизвестными и пусть 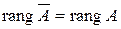 .
.
Определение 7. Число 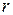 , равное рангу матриц
, равное рангу матриц 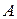 и
и  , называется рангом системы (1).
, называется рангом системы (1).
Не ограничивая общности, будем считать, что базисный минор матрицы 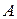 расположен в левом верхнем углу (этого всегда можно добиться применением нумерации неизвестных и перестановкой уравнений). Обозначим этот минор
расположен в левом верхнем углу (этого всегда можно добиться применением нумерации неизвестных и перестановкой уравнений). Обозначим этот минор 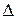 :
:
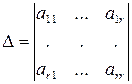 .
.
Минор 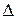 является базисным и для
является базисным и для  , поэтому строки матрицы
, поэтому строки матрицы  с номерами
с номерами 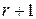 , …,
, …, 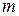 являются линейными комбинациями первых
являются линейными комбинациями первых 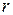 ее строк (теорема о базисном миноре). Это означает, что уравнения с номерами
ее строк (теорема о базисном миноре). Это означает, что уравнения с номерами 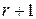 , …,
, …, 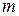 представляют собой линейные комбинации первых
представляют собой линейные комбинации первых 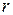 уравнений, так что система (1) эквивалентна системе
уравнений, так что система (1) эквивалентна системе
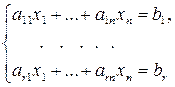 (5)
(5)
(так как все решения (5) обращаются в тождество все последующие уравнения).
Если  , то (5) система с определителем неравным нулю и она (и значит система (1)) имеет единственное решение, определяемое по правилу Крамера. Т.о., справедлива следующая теорема.
, то (5) система с определителем неравным нулю и она (и значит система (1)) имеет единственное решение, определяемое по правилу Крамера. Т.о., справедлива следующая теорема.
Теорема 3. Если 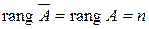 , то система (1) имеет единственное решение.
, то система (1) имеет единственное решение.
Пусть далее  . Оставим в левых частях лишь те слагаемые, коэффициенты которых образуют базисный минор
. Оставим в левых частях лишь те слагаемые, коэффициенты которых образуют базисный минор 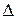 , остальные перенесем вправо.
, остальные перенесем вправо.
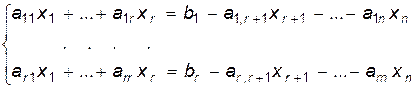 (6)
(6)
Определение 8. Неизвестные  называются базисными, а переменные
называются базисными, а переменные  – свободными.
– свободными.
Свободным переменным можно придать произвольные значения. Тогда базисные неизвестные  определяются по формулам Крамера:
определяются по формулам Крамера:
 ,
, 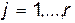
Здесь 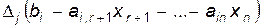 – определитель, получающийся из
– определитель, получающийся из  заменой
заменой  -ого столбца на столбец свободных членов системы (6). Пользуясь свойствами определителя, последнюю формулу можно переписать в виде:
-ого столбца на столбец свободных членов системы (6). Пользуясь свойствами определителя, последнюю формулу можно переписать в виде:
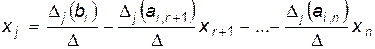 .
.
Введем обозначения: 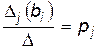 ,
,  .
.
Тогда имеем
 .
.
Добавляя сюда очевидные равенства:  , …,
, …, 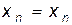 , имеем
, имеем
 (7)
(7)
Формулы (7) дают общее решение системы (1), т. к. выражают все неизвестные 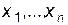 через свободные неизвестные
через свободные неизвестные 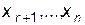 .
.
Покажем, что формулы (7) содержат все варианты решения системы (1). В самом деле, если  ,
, 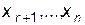 – решение СЛУ (1), то
– решение СЛУ (1), то 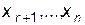 имеют определенные числовые значения Þ подставляя их в систему (1) и повторяя все предыдущие выкладки, получим (7).
имеют определенные числовые значения Þ подставляя их в систему (1) и повторяя все предыдущие выкладки, получим (7).
Таким образом, доказано.
Теорема 4. Если (1) совместна и ее ранг меньше 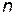 , то эта система имеет бесконечное множество решений.
, то эта система имеет бесконечное множество решений.
Пример. 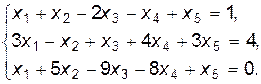
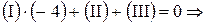
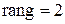 . Возьмем
. Возьмем  ,
,  – базисные Þ из (I) и (II) имеем:
– базисные Þ из (I) и (II) имеем: 
 .
.
5°. Метод Гаусса решения СЛУ.
На практике чаще всего используют метод Гаусса построения решений СЛУ. При этом при исследовании и решении СЛУ производятся элементарные преобразования строк расширенной матрицы  : перестановка строк (это соответствует перестановке уравнений системы), сложение строк (это соответствует сложению уравнений системы), умножение строк на отличное от нуля число (это соответствует умножению уравнения системы на отличное от нуля число). Очевидно, что при указанных преобразованиях получается система, эквивалентная данной. Следовательно, после элементарных преобразований строк расширенной матрицы
: перестановка строк (это соответствует перестановке уравнений системы), сложение строк (это соответствует сложению уравнений системы), умножение строк на отличное от нуля число (это соответствует умножению уравнения системы на отличное от нуля число). Очевидно, что при указанных преобразованиях получается система, эквивалентная данной. Следовательно, после элементарных преобразований строк расширенной матрицы  получается расширенная матрица некоторой новой системы, эквивалентной данной системе.
получается расширенная матрица некоторой новой системы, эквивалентной данной системе.
Замечание. Перестановка в основной матрице двух столбцов соответствует в системе перестановке неизвестных вместе со своими координатами. Умножение столбца на число и сложение столбцов приводит к изменению коэффициентов только при одном неизвестном и значит к системе, не эквивалентной рассматриваемой.
Рассмотрим матрицу  . Элементарными преобразованиями строк ее можно привести к ступенчатой матрице
. Элементарными преобразованиями строк ее можно привести к ступенчатой матрице  :
:  :
:
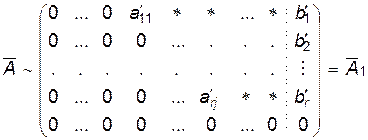
( – некоторый элемент поля
– некоторый элемент поля 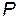 ).
). 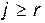 .
.
Выберем в матрице 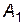 ненулевой минор порядка
ненулевой минор порядка 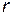 , т.е. базисный минор. Как и в теореме 11, §11 (о ступенчатой матрице), его можно выбрать на пересечении первых
, т.е. базисный минор. Как и в теореме 11, §11 (о ступенчатой матрице), его можно выбрать на пересечении первых 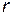 строк и столбцов, с которых начинаются ненулевые элементы строк. Этот минор верхнетреугольный и равен произведению
строк и столбцов, с которых начинаются ненулевые элементы строк. Этот минор верхнетреугольный и равен произведению 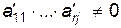 . Будем считать, что этот минор расположен в левом верхнем углу матрицы
. Будем считать, что этот минор расположен в левом верхнем углу матрицы  (перестановкой столбцов матрицы
(перестановкой столбцов матрицы 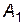 и перенумерацией переменных этого всегда можно добиться). Нулевые строки матрицы отбросим (этому соответствуют уравнения
и перенумерацией переменных этого всегда можно добиться). Нулевые строки матрицы отбросим (этому соответствуют уравнения  с любым решением).
с любым решением). 
 .
.
Далее все элементы базисного минора выше главной диагонали можно сделать равными нулю (как в теореме 11, §11), а элементы главной диагонали – равными 1 (умножением строки на 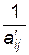 ):
):
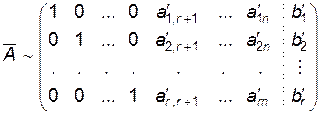
Т.о., исходная система (1) приведена к эквивалентной системе

или к системе

Отсюда видно, что если  , то система имеет единственное решение
, то система имеет единственное решение
 , …,
, …,  .
.
Если 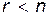 , то переменные
, то переменные  – базисные,
– базисные, 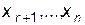 – свободные и придавая им произвольные значения
– свободные и придавая им произвольные значения  , …,
, …, 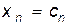 , получим решение:
, получим решение:
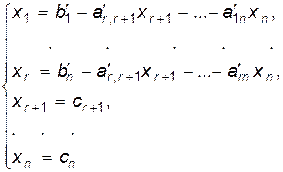 (9)
(9)
или, по аналогии с (7)
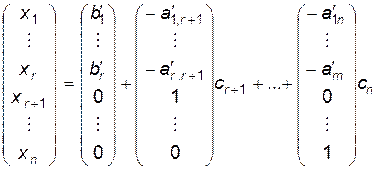 (10)
(10)
По аналогии с п.4 можно показать, что (9), (10) дают общее решение системы (1).
Итак, метод Гаусса состоит в следующем.
1) расширенную матрицу системы элементарными преобразованиями приводят к ступенчатому виду;
2) сравнивают ранги основной и расширенной матриц и делают вывод о совместности или не совместности системы;
3) в случае совместности системы в основной матрице выбирают базисный минор и дальнейшими элементарными преобразованиями строк добиваются того, чтобы в этом миноре все элементы вне главной диагонали стали равными нулю, а элементы главной диагонали стали равными единице;
4) выписывают систему, соответствующую полученной расширенной матрице, после чего переписывают систему, оставляя базисные неизвестные слева и переведя остальные слагаемые в правую часть;
5) если 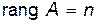 , то в правой части стоят только свободные члены и получено единственное решение;
, то в правой части стоят только свободные члены и получено единственное решение;
6) если 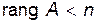 , то в правой части есть свободные неизвестные. Придавая им произвольные значения, получаем общее решение по формуле (9).
, то в правой части есть свободные неизвестные. Придавая им произвольные значения, получаем общее решение по формуле (9).
Пример (см. п.4°).

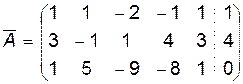 ~
~ 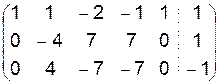 ~
~ 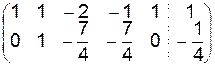 ~
~ 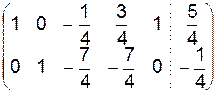

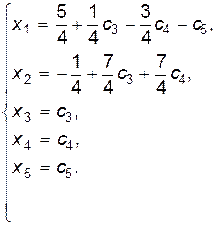
6°. Нахождение обратной матрицы методом Гаусса.
Напомним, что матрица  называется обратной к
называется обратной к 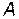 , если
, если 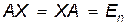 . Обратные матрицы существуют лишь для невырожденных матриц, т.е.
. Обратные матрицы существуют лишь для невырожденных матриц, т.е. 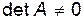 . Было показано, что
. Было показано, что 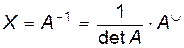 , где
, где  – присоединенная матрица, полученная из алгебраических дополнений, т. е. вычислением определителей
– присоединенная матрица, полученная из алгебраических дополнений, т. е. вычислением определителей  -ого порядка. Вместе с тем, операция вычисления определителя, запрограммированная в ЭВМ, требует больших машинных ресурсов. Поэтому более предпочтительным выглядит вычисление обратной матрицы с помощью метода Гаусса.
-ого порядка. Вместе с тем, операция вычисления определителя, запрограммированная в ЭВМ, требует больших машинных ресурсов. Поэтому более предпочтительным выглядит вычисление обратной матрицы с помощью метода Гаусса.
Для этого воспользуемся определением обратной матрицы 


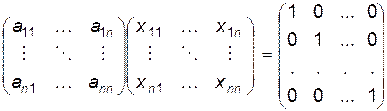


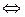
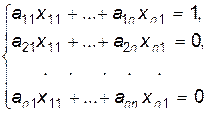
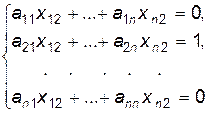
…

Т.о., матричное уравнение  эквивалентно системе линейных уравнений, состоящей из
эквивалентно системе линейных уравнений, состоящей из 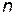 систем, каждая из которых является системой из
систем, каждая из которых является системой из 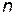 переменных и все они имеют одну и ту же основную матрицу систем:
переменных и все они имеют одну и ту же основную матрицу систем:
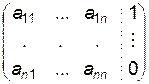 ;
; 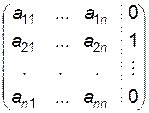 ; …;
; …; 
Все эти системы объединим в одной расширенной матрице:

Приведение этой матрицы к ступенчатому виду должно обозначать приведение к ступенчатому виду всех расширенных матриц подсистем. Так как 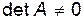

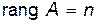
 она может быть приведена к следующему виду
она может быть приведена к следующему виду

Решение каждой из подсистем имеет вид:
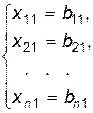 ,
,  , …,
, …, 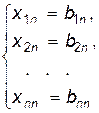

матрица  , стоящая за вертикальной чертой, является обратной матрицей
, стоящая за вертикальной чертой, является обратной матрицей 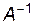 .
.
Пример (см. пример из §8)
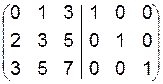 ~
~  ~
~ 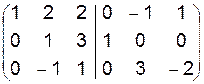 ~
~  ~
~ 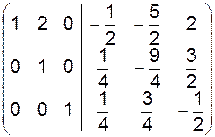 ~
~ 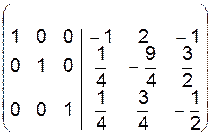
7о. Однородные системы уравнений.
Рассмотрим однородную систему уравнений:
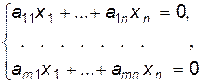
Лемма 1. Система однородных уравнений всегда совместна.
Действительно, 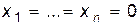 – ее решение. Это решение называется тривиальным.
– ее решение. Это решение называется тривиальным.
Ненулевые решения называются нетривиальными.
В соответствии с общей теорией, справедлива следующая лемма.
Лемма 2. Однородная система с квадратной матрицей 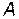 имеет нетривиальное решение
имеет нетривиальное решение 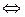
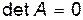 .
.
Доказательство. 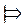 Пусть нетривиальное решение существует, тогда два решения. Методом от противного. Пусть
Пусть нетривиальное решение существует, тогда два решения. Методом от противного. Пусть 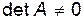
 по формулам Крамера – решение единственное, что противоречит условию
по формулам Крамера – решение единственное, что противоречит условию 
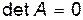 .
.
 Следовательно,
Следовательно, 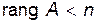
 существуют свободные переменные
существуют свободные переменные  нетривиальное решение.
нетривиальное решение.
Теорема 5. (о множестве решений системы однородных уравнений).
Множество решений СОЛУ образует в пространстве  подпространство размерности
подпространство размерности  , где
, где  .
.
Доказательство. В соответствии с п.4о, решение СОЛУ можно записать в виде (см. формулу (7)):

т.к. 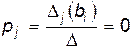 , т. е. в случае СОЛУ, любое решение системы выражается в виде линейной комбинации
, т. е. в случае СОЛУ, любое решение системы выражается в виде линейной комбинации  векторов:
векторов:
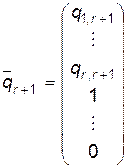 , …,
, …,  .
.
Следовательно, множество всех решений СОЛУ образует подпространство в пространстве  .
.
Теперь покажем, что вектора 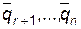 – линейно независимы. Для этого составим матрицу
– линейно независимы. Для этого составим матрицу 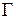 из их координат:
из их координат:

Снизу расположен минор порядка  , отличный от нуля
, отличный от нуля 


 столбцов матрицы
столбцов матрицы 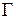 линейно независимы
линейно независимы  вектора
вектора 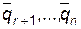 – линейно независимы
– линейно независимы  эти вектора образуют базис подпространства
эти вектора образуют базис подпространства  размерность подпространства равна
размерность подпространства равна  . ч.т.д.
. ч.т.д.
Пусть известны какие-либо  линейно независимых решений СОЛУ:
линейно независимых решений СОЛУ:
 , …,
, …,  .
.
Тогда, в силу предыдущей теоремы, эти вектора образуют базис в подпространстве всех решений СОЛУ и любое решение может быть представлено в виде линейной комбинации этих векторов
 ,
, 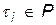 . (11)
. (11)
и обратно, любая линейная комбинация дает решение СОЛУ.
Определение 9. Всякая линейно независимая система  решений СОЛУ (1) называется фундаментальной системой решений.
решений СОЛУ (1) называется фундаментальной системой решений.
Т.о., для того, чтобы решить СОЛУ, надо найти фундаментальную систему решений. Тогда общее решение задается формулой (11), где 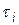 – произвольные элементы
– произвольные элементы 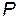 .
.