Частные случаи матриц.

1. Если , то матрица называется квадратной. Её диагональ называется главной диагональю, а – побочной диагональю.

2. Диагональная матрица – это матрица, у которой все ненулевые элементы находятся на главной диагонали, т.е. .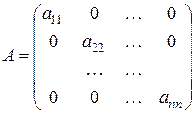

3. Диагональная матрица вида 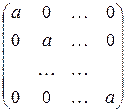называется скалярной.

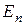4. Скалярная матрица с единичными элементами на главной диагонали называется единичной. Обозначается или , где 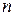– ее порядок.

5. Матрица размера 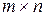, у которой все элементы равны нулю, называется нулевой и обозначается .

6. Если 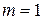, то матрица называется строкой, или матрица-строка, или строка. Если столбцовая = матрица-столбец = столбец.

Определение 2. Две матрицы называются равными, если эти матрицы имеют одинаковые порядки и их соответствующие элементы совпадают.

2^о. Операции над матрицами и их свойства.

Определение 3. Суммой матриц 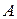и 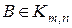(т.е. имеющих одинаковые порядки) называется матрица : .

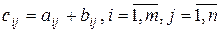Обозначение: .

Замечание. Сумма матриц – алгебраическая операция.