Объединение множеств.

Множества А и В входят в их объединение только один раз. Это вполне соответствует толкованию множества, принятому в математике: ни один элемент не может содержаться в множестве несколько раз.

Определение 1.5

Объединением двух множеств А и В называется такое множество С, которое состоит из всех тех элементов, которые принадлежат хотя бы одному из множеств А или В.

Символически объединение двух множеств А и В обозначается так:

А È В, где È - символ объединения множеств. Определение 1.5 можно записать с помощью характеристического свойства:

С= А È В={xï xÎ A или xÎ B}. (4)

Союз “или” иногда заменяют квадратной скобкой

(5)

а также знаком дизъюнкции

х Î А È В Þ хÎ А Ú хÎ В. (5а)

Читаются эти знаки одинаково: если элемент х принадлежит объединению двух множеств А и В, то он принадлежит множеству А или множеству В.

Если же элемент х не принадлежит объединению множеств А и В, то он не принадлежит ни множеству А, ни множеству В. Символически это может быть записано так:

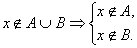(6)

или

x Ï AÈ B Þ xÏ A Ù xÏ B. (6а)

Графически варианты объединения двух множеств показаны на рис. 11\14 (объединение заштриховано).

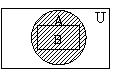
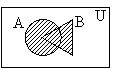
рис. 11 рис. 12 рис. 13 рис. 14

Отметим некоторые очевидные свойства операции объединения двух множеств:

АÈ А=А, АÈ Æ =А, АÈ U=U. (7)

Замечание1.

Если А₁, А₂, …, А_n – несколько множеств, то аналогично тому, как это делалось для двух множеств, определяется их пересечение, т.е. составляется множество, представляющее их общую часть:

Р= А₁Ç А₂Ç …Ç А_n={x ï xÎ " A_i, i= },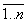

Где символ " (квантор всеобщности) заменяет слово “все”, и, таким образом, мы символически обозначили ту часть множеств A_i, которая принадлежит каждому множеству одновременно.

Замечание 2.

Если А₁, А₂, …, А_n – несколько множеств, то аналогично тому, как это делалось для двух множеств, определяется их объединение – составляется множество, состоящее из элементов, которые принадлежат хотя бы одному их них:

C= A₁È A₂È …È A_n={x ï xÎ A₁ или xÎ A₂ или …или xÎ A_n}.

Замечание 3.

Если в выражении есть знаки È и Ç и нет скобок, то сначала выполняется операция пересечения, а потом – операция объединения (аналог сложению и умножению в арифметике).