
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ТЕМА №1. Множества и операции над ними.
|
|
АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
8935 - землеустройство
ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ
Целью курса является знакомство студентов с фундаментальными методами алгебры и аналитической геометрии.
ТРЕБОВАНИЯ К УРОВНЮ ОСВОЕНИЯ СОДЕРЖАНИЯ ДИСЦИПЛИНЫ
В результате изучения курса студент усвоить методику построения алгебраических структур, внутреннюю логику, связывающую линейную алгебру и аналитическую геометрию, и приобрести навыки исследования и решения задач алгебры и аналитической геометрии.
ОБЪЕМ ДИСЦИПЛИНЫ И ВИДЫ УЧЕБНОЙ РАБОТЫ
| Вид учебной работы | Всего часов | Семестры |
| Общая трудоемкость | 1, 2 | |
| Аудиторные занятия | ||
| Лекции | ||
| Практические занятия (семинары) | ||
| Лабораторные работы | – | |
| Самостоятельная работа | ||
| Курсовые работы/рефераты | ||
| Вид итогового контроля: экзамен | зачет |
СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
4.1 РАЗДЕЛЫ ДИСЦИПЛИНЫ И ВИДЫ ЗАНЯТИЙ
| № п/п | Наименование тем и разделов | Всего | Аудиторные занятия | Самостоятельная работа |
| Алгебра | ||||
| Аналитическая геометрия | ||||
| ИТОГО |
ВВЕДЕНИЕ
Предмет дисциплины «Геометрия и алгебра». Исторические сведения о развитии этого раздела математики. Роль и место геометрии и алгебры в системе математического образования.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Простейшие задачи аналитической геометрии. Векторная алгебра. Аффинные координаты. Формулы преобразования координат.
Уравнение линии. Уравнение поверхности. Линейные образы на плоскости и в пространстве. Различные виды задания уравнений прямой и плоскости. Углы между прямыми и плоскостями. Условия параллельности и перпендикулярности прямой и плоскостей. Расстояния между точкой и прямой, точкой и плоскостью.
АЛГЕБРА
Множество. Отображения. Бинарные отношения. Отношение эквивалентности.
Матрицы, операции над ними. Элементарные преобразования матрицы и матрицы элементарных преобразований. Определители, их свойства. Теорема Лапласа. Обратная матрица. Критерий обратимости матрицы. Ранг матрицы, теорема о базисном миноре. Исследование систем линейных алгебраических уравнений. Правило Крамера. Метод Гаусса.
Линейное пространство. Линейная зависимость векторов. Конечномерные линейные пространства, базис и размерность. Преобразование координат вектора при изменении базиса. Линейные подпространства, линейные оболочки. Линейные многообразия. Геометрические свойства множества решений системы линейных алгебраических уравнений с точки зрения фактов линейного пространства.
ЛИТЕРАТУРА
1. Атанасян Л.С., Базылев В.Т. Геометрия. Часть I.- М.: Просвещение, 1986.
- Атанасян Л.С., Базылев В.Т. Геометрия. Часть П.- М.: Просвещение, 1987.
- Атанасян Л.С., Атанасян В.А. Сборник задач по геометрии.- Часть 1.- М.: Просвещение, 1973.
- Базылев В.Т. и др. Сборник задач по геометрии.- М.: Просвещение, 1980.
- Курош А.Г. Курс высшей алгебры: Учеб. М.: Наука, 1975.431 с.
- Ильин В.А., Позняк Э.Г. Аналитическая геометрия: Учеб. М.: Наука, 1988. 232 с.
- Ильин В.А., Позняк Э.Г. Линейная алгебра: Учеб. М.: Наука, 1984.295 с.
- Ильин В.А., Ким Г.Д. Линейная алгебра и аналитическая геометрия: Учеб. М.: Изд-во Моск. ун-та, 1998. 320 с.
- Проскуряков И.В. Сборник задач по линейной алгебре: Учеб. пособие. М.: Наука, 1984.336 с.
- Бахвалов С.В., Моденов П.С., Пархоменко А.С. Сборник задач по аналитической геометрии: Учеб. пособие. М.: Наука, 1964. 440 с.
- Икрамов Х.Д. Задачник по линейной алгебре: М.: Наука, 1975. 320 с.
- Роджерс Д., Адаме Дж. Математические основы машинной графики: М.: Машиностроение, 1980.
- Атанасян Л.С., Васильева М.В., Вересова Е.Е., Гуревич Г.Б., Ильин А.С., Лактанова Н.В., Редозубова О.С. Сборник задач по геометрии.- Часть 2.- М.: Просвещение, 1975.
Теоретические сведения
ТЕМА №1. Множества и операции над ними.
§1. Основные понятия о множествах.
1.1. Основные определения.
Одним из основных понятий математики является понятие множества, и, как каждое основное понятие, не поддаётся точному определению (например, понятия “точка”, “прямая” являются одними из основных понятий геометрии).
МНОЖЕСТВОМ называется собрание, совокупность объектов, объединенных по какому-нибудь общему признаку, свойству.
Примеры:
1. Множество студентов данной учебной группы.
2. Множество планет солнечной системы.
3. Множество букв русского алфавита.
4. Множество натуральных чисел.
Математический смысл слова “множество” отличается от того, как оно используется в обычной речи. Так, в обычной речи понятие “множество” связывают с большим числом предметов, в математике же этого не требуется. Здесь могут рассматриваться множества, содержащие один объект, много объектов, несколько объектов или не содержащие ни одного объекта.
Объекты, из которых состоит множество, называются его ЭЛЕМЕНТАМИ.
Остановимся на символике, обычно использующейся при обращении с множествами.
Множества обозначаются прописными (заглавными) буквами латинского алфавита (без индексов или с индексами). Например: B, C, …, X, Y, …, A1, B1, …
Элементы множества обозначаются строчными (малыми) буквами латинского алфавита. Например: b, c, …, x, y, …, a1, b1, …
В математике особую роль играют множества, элементами которых являются числа. Такие множества называются ЧИСЛОВЫМИ. Некоторые числовые множества имеют специальные обозначения, вводимые для удобства пользования. Один из вариантов этих обозначений, которыми мы будем пользоваться в дальнейшем, выглядит следующим образом:
N – множество всех натуральных чисел;
Zc (или Z+ или C+) – множество всех целых неотрицательных чисел;
Z (или C) – множество всех целых чисел;
Q – множество всех рациональных чисел;
R – множество всех действительных чисел;
R+ - множество всех действительных положительных чисел.
По числу элементов, входящих в множество, множества делятся на три класса:
1 – конечные, 2 – бесконечные, 3 – пустые.
1. Если элементы множества можно сосчитать, то множество является КОНЕЧНЫМ.
Пример 1.
Множество гласных букв в слове “математика” состоит из трёх элементов – это буквы “а”, “е”, “и”, причем, гласная считается только один раз, т.е. элементы множества при перечислении не повторяются.
2. Если элементы множества сосчитать невозможно, то множество БЕСКОНЕЧНОЕ.
Пример 2.
Множество натуральных чисел бесконечно.
Пример 3.
Множество точек отрезка [0; 1] бесконечно.
3. Множество, не содержащее ни одного элемента, называется ПУСТЫМ. Символически оно обозначается знаком Æ.
Пример 4.
Множество действительных корней уравнения x2 +1=0.
Пример 5.
Множество людей, проживающих на Солнце.
В математике часто приходится определять принадлежность данного элемента конкретному множеству.
Пример 6.
Мы говорим, что число 5 натуральное, т.е. утверждаем, что число 5 принадлежит множеству натуральных чисел. Символически принадлежность множеству записывается с помощью знака Î. В данном случае символическая запись будет такой: 5 Î N. Читается: “5 принадлежит множеству натуральных чисел”.
Число 5, 2 не принадлежит множеству натуральных чисел, т.к. не является натуральным числом. Символически отношение “не принадлежит” записывается с помощью знака 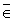 (реже Ï). Таким образом, здесь имеем: 5, 2 Ï N
(реже Ï). Таким образом, здесь имеем: 5, 2 Ï N
Читается: “5, 2 не принадлежит множеству натуральных чисел”.