
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример.
|
|
 ;
; 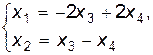
 ~
~  .
.
 ,
, 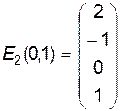 .
.
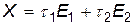 .
.
Теперь покажем, что любое подпространство  пространства
пространства  может быть получено как решение некоторой СОЛУ.
может быть получено как решение некоторой СОЛУ.
Теорема 6. Всякое подпространство  размерности
размерности  в пространстве
в пространстве  с данным базисом является подпространством решений некоторой системы линейных однородных уравнений ранга
с данным базисом является подпространством решений некоторой системы линейных однородных уравнений ранга  .
.
Доказательство. Пусть в  задан базис
задан базис  и подпространство
и подпространство  . Возьмем в
. Возьмем в  базис
базис  дополним его до базиса в
дополним его до базиса в  :
: 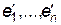 . Каждый вектор
. Каждый вектор  можно разложить оп этому базису
можно разложить оп этому базису
 ,
,
причем 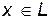
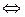
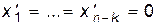 , т.к.
, т.к.  – линейная оболочка
– линейная оболочка  . Уравнения
. Уравнения 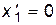 , …,
, …,  определяют
определяют  в базисе
в базисе 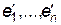 . Известно, что два базиса связаны формулами:
. Известно, что два базиса связаны формулами:  , где
, где  – матрица перехода,
– матрица перехода,  . Тогда
. Тогда  – формула связи координат вектора в различных базисах. Следовательно,
– формула связи координат вектора в различных базисах. Следовательно,  и система уравнений на
и система уравнений на  имеет вид
имеет вид
 ,
,  (12)
(12)
Т.к. 
 строки матрицы
строки матрицы  линейно независимы
линейно независимы  ранг системы (12) равен
ранг системы (12) равен  . ч.т.д.
. ч.т.д.
8о. системы линейных неоднородных уравнений
Рассмотрим систему неоднородных уравнений
 (13)
(13)
Пусть  . Пусть
. Пусть 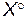 – решение этой системы, т.е.
– решение этой системы, т.е.
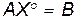 (14)
(14)
Вычитая из (13) выражение (14), получаем
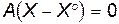 .
.
Т.о., 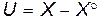 является решением соответствующего однородного уравнения.
является решением соответствующего однородного уравнения.
Пусть  – фундаментальная система решений однородного уравнения. Тогда любое
– фундаментальная система решений однородного уравнения. Тогда любое 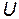 может быть представлено в виде:
может быть представлено в виде:
 .
.
Тогда получаем
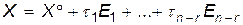 (15)
(15)
Если 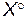 – частное решение уравнения (13), то формулы (15) дают общее решение. Из (15) следует теорема.
– частное решение уравнения (13), то формулы (15) дают общее решение. Из (15) следует теорема.
Теорема 7. Общее решение СЛНУ (13) представляется в виде суммы произвольного частного решения этой системы и общего решения соответствующей ей однородной системы.
Следствие 1. Разность двух произвольных решений СЛНУ является решением соответствующей СЛОУ.
Следствие 2. Сумма любого частного решения СЛНУ с любым частным решением соответствующей СЛОУ дает частное решение СЛНУ.
Замечание. В формуле (7) вектор 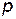 – частное решение СЛНУ, а вектора
– частное решение СЛНУ, а вектора  – частные решения СЛОУ.
– частные решения СЛОУ.
Тема 4. Линейное пространство
 1о. Определение и простейшие свойства
1о. Определение и простейшие свойства
Пусть даны поле  с элементами, называемыми скалярами и обозначаемыми малыми греческими буквами
с элементами, называемыми скалярами и обозначаемыми малыми греческими буквами  ,
,  ,
,  , … и множество
, … и множество  элементов, называемых векторами и обозначаемых латинскими буквами
элементов, называемых векторами и обозначаемых латинскими буквами 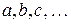 . Введем на
. Введем на  алгебраическую операцию сложения, которая каждой паре элементов
алгебраическую операцию сложения, которая каждой паре элементов  ставит в соответствие третий элемент
ставит в соответствие третий элемент  , называемый суммой
, называемый суммой  и
и 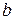 и обозначаемый
и обозначаемый  , а также операцию умножения скаляра на вектора, которая
, а также операцию умножения скаляра на вектора, которая  и
и 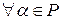 ставится в соответствие
ставится в соответствие  , называемый произведением вектора
, называемый произведением вектора 
 на скаляр
на скаляр  и обозначаемый
и обозначаемый 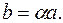
Определение 1. Множество  вместе с заданными на нем операциями сложения векторов и умножения вектора на скаляр называется линейным (векторным) пространством над полем
вместе с заданными на нем операциями сложения векторов и умножения вектора на скаляр называется линейным (векторным) пространством над полем  , если удовлетворяются следующие аксиомы:
, если удовлетворяются следующие аксиомы:
1) 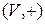 является абелевой группой;
является абелевой группой;
2) Для любых 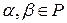 и
и  выполняются равенства:
выполняются равенства:
а) Умножение 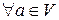 на
на 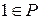 не изменяет
не изменяет  , т.е.
, т.е.  .
.
б) 


 .
.
в) Умножение вектора на скаляр дистрибутивно относительно сложения скаляров, т.е. 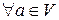


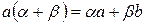 .
.
г) Умножение вектора на скаляр дистрибутивно относительно сложения векторов, т.е. 
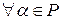

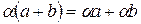 .
.