
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение кривых свободной поверхности
|
|
На практике построение кривых свободной поверхности потоков осуществляется при проектировании различных сооружений – водопропускных, гидротехнических, водозаборных и т.д.
Поставленная задача будет решена, если в любом сечении на интересующем нас участке возможно определить глубину потока. Для наглядного представления о поведении кривых свободной поверхности обычно получают достаточное количество расчётных точек и соединяют их плавной кривой. Рассмотрим один из методов построения кривых подпора и спада – метод непосредственного применения уравнения Бернулли. Весь участок, на котором необходимо построить кривую свободной поверхности, разбивают на ряд расчетных участков (протяженность этих участков может быть до десятков метров). Запишем уравнение Бернулли для первого (например, от перепада или от плотины) участка, ограниченного сечениями 1-1 и 2-2, в результате отметка  известна:
известна:
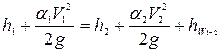 . (16.2)
. (16.2)
Потери напора на этом участке определяются по формуле Шези:
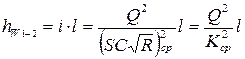 ,
,
где значение  можно определить, например, как среднеарифметическое значение
можно определить, например, как среднеарифметическое значение
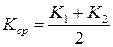 . (16.3)
. (16.3)
После подстановки (16.3) в уравнение (16.2) получим для участка длиной 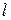 (эта длина была нами назначена)
(эта длина была нами назначена)
 (16.4)
(16.4)
Из этого уравнения методом последовательных приближений определяется 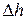 (или
(или 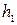 ). После определения
). После определения 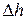 (определив отметку свободной поверхности
(определив отметку свободной поверхности 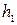 ) переходят к расчету следующего участка, пользуясь теми же уравнениями. Определив таким образом несколько глубин, строят кривую свободной поверхности.
) переходят к расчету следующего участка, пользуясь теми же уравнениями. Определив таким образом несколько глубин, строят кривую свободной поверхности.