Программа для ЭВМ.

На рис. 6.2 изображена блок-схема программы проведения экспериментов на ЭВМ с нашей моделью фирмы. Блок-схема делает n повторений (реплик) для каждого плана. Каждая реплика — это просчет модели в течение ТМ единиц времени. В результате каждого просчета вычисляется полная прибыль

ПРИБЫЛЬ = Q× (P - С), (6.18)

где Р - цена, Q - число единиц продукции, произведенной в течение периода ТМ, С - удельные затраты. В блок-схеме (и машинной программе) предполагается, что в ЭВМ есть подпрограмма, генерирующая экспоненциальное распределение с отрицательным показателем и заданным математическим ожиданием.

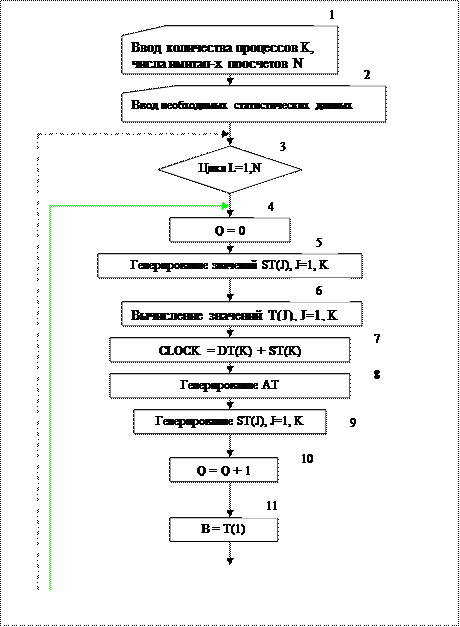
Рис. 6.2. Блок-схема расчета модели фирмы.

Блок 1 на рис. 6.2 описывает ввод в ЭВМ параметров К (общее число процессов в модели) и N (число повторений имитационного просчета). В память машины вводятся значения Р, С, ТМ, ЕАТ и ЕSТj (j =1, …, k). Эти величины служат параметрами данного плана. Заметим, что на блок-схеме величина SТj обозначена SТ(J) в соответствии с требованиями машинного языка ФОРТРАН. В блоках 3 и 4 осуществляются начальные процедуры, в которых величине L (указатель номера реплики) присваивается 1, а величине Q (число единиц готовой продукции) присваивается 0. В блоке 5 подпрограммой экспоненциального распределения с отрицательным показателем генерируются величины затрат времени на производство. Затем по формулам (6.7) - (6.9) подсчитываются времена простоя, ожидания и полное время пребывания первого заказа в каждом производственном процессе.

В программе используется системное время СLOСК. В блоке 7 эта величина подсчитывается как сумма времени простоя и времени, затраченного на производство, для K-го процесса. К концу планового периода системное время становится не меньше продолжительности периода ТМ. Блок 8 генерирует промежуток времени АТ между поступлениями первого и второго заказов. Таким образом, этот блок дает указание о поступлении второго заказа. После этого в блоке 9 генерируется K новых величин затрат времени на производство. Блок 10 увеличивает общее число выполненных заказов на 1.

В блоках 11 и 12 величинам B и D присваиваются значения T(1) и АТ соответственно. Блоки от 13 до 21 повторяются K раз — по одному для каждого производственного процесса. В блоке 14 по формулам (7.11) вычисляются разности WТ(J), играющие роль DIF(J). Если WT(J)> 0, то время простоя равно нулю, а время ожидания равно NT(J). Если WT(J)=0, то и время ожидания, и время простоя равны нулю. Если же WT(J)< 0, то время ожидания равно нулю, а время простоя равно WT(J). В блоке 19 по формулам (6.10) для j-го процесса подсчитывается значение Т (J). Величины B и D пересчитываются в блоках 20 и 21 по формулам (6.11). Системное время СLOСК пересчитывается в блоке 22.

Если время СLOСК меньше ТМ, происходит обращение к блоку 8 и генерируется еще один промежуток времени между поступлениями заказов и K величин затрат времени на производство. Если же системное время СLOСК не меньше ТМ, то закончена одна реплика расчета первого плана. Полная прибыль в этой реплике подсчитывается по формуле (6.18) и выводится на печать. Если число реплик L меньше числа необходимых просчетов N для этого плана, то L увеличивается на 1 и с блока 4 начинается новая реплика.

1 READ 2, K, N

2 FORMAT(2I2)

3 DIMENSION EST(K), ST(K), T(K), WT(K), DT(K)

4 READ 5, P, C, TM, EAT, (EST(J), J = 1, K)

5 FORMAT(10F10.2)

6 L = 1

7 Q = 0.

8 DO 10 J = 1, K

9 CALL RAND (R)

10 ST(J) = -EST(J)*LOGF(R)

11 K1 = K - 1

12 DT(1) = 0.

13 DO 14 J=1, K1

14 DT(J+1)=DT(J) + ST(J)

15 DO 17 J=1, K

16 WT(J) = 0.

17 T(J) = ST(J)

18 CLOCK = DT(K) + ST(K)

19 CALL RAND (R)

20 AT = - EAT*LOGF(R)

21 DO 23 J = 1, K

22 CALL RAND (R)

23 ST(J)= - EST(J)*LOGF(R)

24 Q = Q+1.0

25 B = T(1)

26 D = AT

27 DO 37 J = 1, K

28 WT(J)=B - D

29 IF(WT(J)) 30, 30, 33

30 DT(J)= - WT(J)

31 WT(J) = 0.

32 GO TO 34

33 DT(J) = 0.

34 T(J) = WT(J) + ST(J)

35 B = B + T(J + 1)

36 D = D + WT(J) + ST(J)

37 CONTINUE

38 CLOCK = CLOCK+ DT(K) + ST(K)

39 JF(CLOCK —TM) 19, 40, 40

40 PROFIT =P*Q - C

41 PRINT 42, PROFIT

42 FORMAT(F10.2)

43 IF(L - N) 44, 4, 4

44 L = L + 1

45 GO TO 7

46 END

Рис. 6.З. Программа машинной модели фирмы.

Если же L ³ N, то расчет по данному варианту окончен и блок 2 считывает параметры следующего расчета.

Программа на языке ФОРТРАН, соответствующая блок-схеме рис. 6.2, приведена на рис. 6.3. Строки программы соответствуют блокам схемы, поэтому нет необходимости заново объяснять логическую схему программы. Сделаем лишь краткое замечание о подпрограмме генерирования экспоненциально распределенных случайных величин.

Говорят, что случайная величина X имеет экспоненциальное распределение, если ее функция плотности вероятностей равна

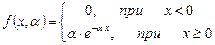. (6.19)

где a> 0, x ³ 0.

Кумулятивная функция распределения случайной величины X имеет вид

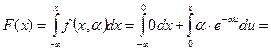
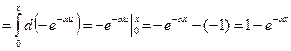, (6.20)

а математическое ожидание и дисперсия задаются формулами

, (6.21)

. (6.22)

Так как экспоненциальное распределение содержит единственный параметр a, его можно выразить через математическое ожидание:

a = 1/MX. (6.23)

Экспоненциально распределенную случайную величину можно генерировать несколькими способами. Так как F(х) выражается в явном виде, обратное преобразование дает простой способ решения задачи. Поскольку равномерное на интервале (0, 1) распределение симметрично относительно точки 0, 5, в формуле обратного преобразования вместо F(х) можно взять 1-F(х), Поэтому вместо

можно взять

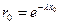, (6.24)

и, следовательно,

. (6.25)

Таким образом, для каждого псевдослучайного числа r определяется единственное значение величины х. Последняя принимает лишь неотрицательные значения (так как ln(r) £ 0 для 0£ г£ 1) и аппроксимирует экспоненциальную функцию плотности вероятностей (6.19) с заданным математическим ожиданием MХ. Этот метод выглядит очень простым, но он требует довольно трудоемкого вычисления на ЭВМ натурального логарифма для каждого генерированного значения равномерно распределенной величины. Для генерирования экспоненциально распределенной величины нужны две команды на языке ФОРТРАН:

CALL RAND(R), (6.26)

X= - EX*LOGF(R), (6.27)

где подпрограмма RAND генерирует значения случайной величины, распределенной равномерно на интервале (0, 1), а подпрограмма LOGF находит натуральный логарифм числа. Обе подпрограммы есть почти во всех используемых в настоящее время ЭВМ. Вызов подпрограмм генерирования экспоненциально распределенной величины встречается в строках 9 и 10, 19 и 20, 22 и 23. Эти строки соответствуют блокам 5, 8 и 9 на рис. 6.2.