
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модель Леонтьева.
|
|
Лекция №3
Применение матриц в задачах межотраслевого баланса.
Основные понятия темы:
1. Модель Леонтьева многоотраслевой экономики. Матрицы коэффициентов прямых и полных затрат, их экономический смысл. Уравнение зависимости между валовой и конечной продукцией.
2. Модель равновесных цен.
Модель Леонтьева.
Цель балансового анализа – ответить на вопрос, связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производства каждой из n отраслей, чтобы удовлетворить все потребности в продукции этой отрасли? Связь между отраслями отражается в таблице межотраслевого баланса, а математическая модель, позволяющая их анализировать, разработана в 1936 г. американским экономистом В. Леонтьевым.
Предположим, что рассматривается n отраслей промышленности, каждая из которых производит свою продукцию.
Продукция каждой отрасли идет на:
1) внутрипроизводственное потребление
(используется в качестве сырья, полуфабрикатов и средств производства в других отраслях, в том числе и в данной);
2) внепроизводственное потребление (конечный продукт Y – используется для накопления и возмещения основных фондов, прироста запасов, на личное потребление и обслуживание населения, оборону, экспорт и т.д.).
Рассмотрим математическую модель (ММ) межотраслевого баланса производства и распределения продукции в народном хозяйстве в стоимостном выражении за один отчетный период времени (например, год).
| Потребляющие отрасли 1 2 … n | Конечная продукция | Валовая продукция | ||
| Производящие отрасли | . . . n | x 11 x 12 … x 1n x 21 x 22 … x 2n … … … … 1-й квадрант x n1 x n2 … x nn | Y 1 Y 2 … 2-й квадрант Y n | X 1 X 2 … X n |
| Оплата труда Чистый доход | V m | V1 V2 … Vn 3-й квадрант m1 m2 … mn | Vкон 4-й квадрант mкон | |
| Валовая продукция | X | X1 X2 … Xn | X |
Введем следующие обозначения:
Xi – общий (валовой) объем продукций i -ой отрасли (i = 1, 2, …, n)
i - номер любой производящей отрасли; j - номер любой потребляющей отрасли.
xij - стоимость части продукции (средств производства), произведенной в i -й отрасли и потребляемой в качестве материальных затрат в j -й отрасли для производства ее валовой продукции (i, j=1, 2, …, n).
Yi –затраты продукции i -ой отрасли вне сферы материального производства, т.е. для целей конечного потребления (удовлетворение спроса населения, накопление, экспорт, военные нужды) для непроизводственного потребления.
В столбцах межотраслевого баланса отражается структура материальных затрат и чистой продукции каждой отрасли.
Так первый столбец x11, x12,..., x1n характеризует структуру материальных затрат 1-й отрасли за отчетный год. Элемент x11 показывает стоимость продукции 1-й отрасли для собственных нужд, x21 отражает затраты на продукцию 2-й отрасли для нужд 1-й отрасли. Кроме материальных затрат, в балансе отражена чистая продукция отраслей. Так, чистая продукция 1-й отрасли характеризуется суммой оплаты труда V1 и чистого дохода (прибыли) m1. Сумма материальных затрат и чистой продукции равна валовой продукции отрасли.
Можно записать систему уравнений по столбцам:
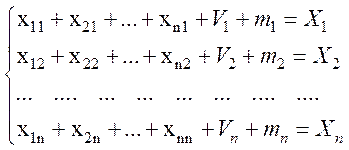
В строках межотраслевого баланса содержатся данные о распределении годового объема продукции каждой отрасли материального производства.
Т.к. валовой объем продукции любой i - ой отрасли равен суммарному объему продукции, потребляемой n отраслями, и конечного продукта, то по данным строк можно составить следующую систему уравнений
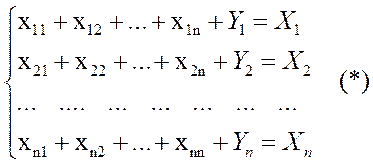
Уравнения (*) называются соотношениями баланса.
В схеме баланса выделяют четыре части, которые называются квадрантами балансами.
В 1 -м квадранте содержатся межотраслевые потоки средств производства. По форме он представляет собой квадратную матрицу. Данные 1 -го квадранта играют важную роль в анализе структуры материальных затрат отраслей.
Во 2 -м квадранте представлена конечная продукция всех отраслей материального производства, т.е. продукция, выходящая из сферы производства в область конечного использования – на потребление и накопление. Таким образом, данные 2-го квадранта характеризуют отраслевую материальную структуру национального дохода.
Показатели 3 -го квадранта также характеризуют национальный доход со стороны его стоимостного состава как сумму оплаты труда и чистого дохода всех отраслей материального производства.
4 -й квадрант отражает конечное распределение и использование национального дохода.
Введем коэффициенты прямых затрат
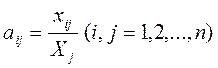
показывающие затраты продукции i-ой отрасли на производство единицы продукции j -ой отрасли. Можно полагать, что в некотором промежутке времени коэффициенты 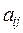 будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат от валового выпуска, т.е.
будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат от валового выпуска, т.е.
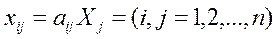 ,
,
вследствие чего построенная на этом основании модель межотраслевого баланса получила название линейной.
Теперь соотношение баланса (*) примут вид:
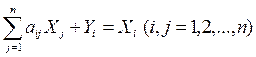
Обозначим
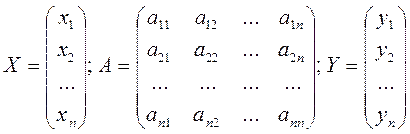 ,
,
Где X - вектор валового продукта, Y - вектор конечного продукта, A - матрица прямых затрат (технологическая или структурная матрица). Все элементы 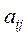 матрицы A неотрицательны и
матрицы A неотрицательны и 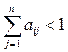 .
.
Тогда систему (*) можно записать в матричном виде:
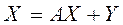 (3.1)
(3.1)
Уравнение (3.1) представляет собой систему балансовых уравнений, описывающую экономико-математическую модель межотраслевого баланса (модель В.В. Леонтьева).
Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска X, который при известной матрице прямых затрат А обеспечивает заданный вектор конечного продукта Y.
Перепишем уравнение (3.1) в виде:
(E-A)X=Y, (3.2)
где  .
.
Матрица (E-A) называется матрицей Леонтьева.
Если матрица (E-A) невырожденная, т.е. 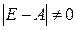 , то по формуле матричного метода
, то по формуле матричного метода 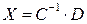 (для системы
(для системы 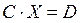 )
)
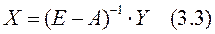
Получаем уравнение, которое выражает зависимость валовой продукции каждой отрасли от конечной продукции всех отраслей.
Обозначим 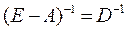 , а ее элементы через dij, тогда
, а ее элементы через dij, тогда
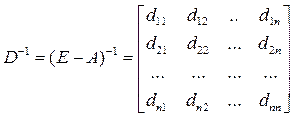
Матрица 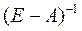 называется матрицей коэффициентов полных затрат.
называется матрицей коэффициентов полных затрат.
Элементы dij (i=1, …, n; j=1, …, n) называются коэффициентами полных материальных затрат. Они включают в себя как прямые, так и косвенные затраты продукции отрасли i на единицу продукции отрасли j.
Если прямые затраты отражают количество средств производства, израсходованных непосредственно при изготовлении данного продукта, то косвенные относятся к предшествующим стадиям производства и входят в продукт не прямо, а через другие средства производства.
Матрица коэффициентов косвенных затрат:
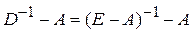
Коэффициенты полных затрат можно использовать и при планировании на следующий отчетный период. Например, если конечную продукцию j-й отрасли увеличить на 1 единицу, то при этом валовый выпуск всех отраслей изменится соответственно на величины d1j, d2j, …, dnj, которые являются элементами j–го столбца матрицы коэффициентов полных затрат  . Положив j=1, 2, …, n, это утверждение можно распространить на все отрасли.
. Положив j=1, 2, …, n, это утверждение можно распространить на все отрасли.
Матрица 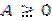 называется продуктивной, если для любого вектора
называется продуктивной, если для любого вектора  существует решение
существует решение 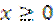 уравнения (3.2). В этом случае и модель Леонтьева продуктивна.
уравнения (3.2). В этом случае и модель Леонтьева продуктивна.
 Существует несколько критериев продуктивности матрицы А. Один из них говорит о том, что матрица А продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, т.е. матрица А продуктивна, если
Существует несколько критериев продуктивности матрицы А. Один из них говорит о том, что матрица А продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, т.е. матрица А продуктивна, если 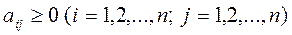 и
и 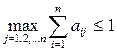 , и существует номер j такой, что
, и существует номер j такой, что  .
.
В таблицу межотраслевого баланса, кроме производственных затрат можно включить затраты труда, капиталовложений и т.д. Они заносятся в таблицу как (n+1)-я, (n+2)-я, … дополнительные строки. Тогда xn+1, j выражают дополнительные затраты труда в j–ю отрасль, а xn+2, j (j=1, 2, …, n) –затраты капиталовложений.
Введем в рассмотрение коэффициенты прямых затрат труда 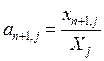 и капиталовложений
и капиталовложений 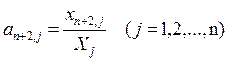 .
.
Дописав эти коэффициенты в виде дополнительных строк в матрицу A, получим прямоугольную матрицу коэффициентов прямых затрат 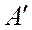 :
:
При решении балансовых уравнений используется лишь основная часть матрицы 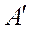 (матрица A). При расчетах же затрат труда и капиталовложений, необходимых для выпуска данного конечного продукта, принимают участие и дополнительные строки.
(матрица A). При расчетах же затрат труда и капиталовложений, необходимых для выпуска данного конечного продукта, принимают участие и дополнительные строки.
Суммарные затраты труда, необходимые для производства единицы конечного продукта j- ой отрасли, равны:
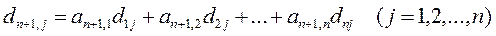 .
.
Эти величины называются коэффициентами полных затрат труда.
Суммарные затраты капиталовложений, необходимые для производства единицы конечного продукта j- ой отрасли, равны:
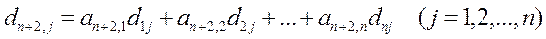 .
.
Эти величины называются коэффициентами полных затрат капиталовложений.
Дополнив матрицу 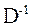 строками dn+1, j, dn+2, j, получим расширенную матрицу коэффициентов полных затрат:
строками dn+1, j, dn+2, j, получим расширенную матрицу коэффициентов полных затрат:
Пользуясь этой матрицей, можно рассчитать при любом заданном ассортименте конечной продукции Y не только необходимый валовый выпуск продукции X, но и необходимые затраты труда Xn+1, капиталовложений Xn+2:
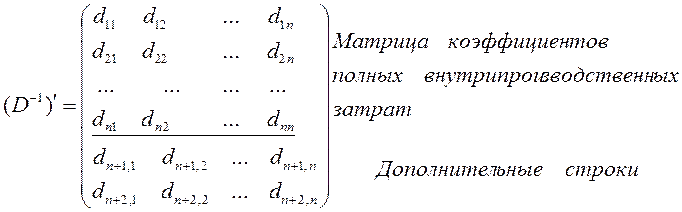
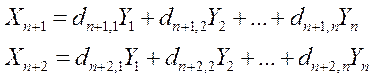 ,
,
т.е. суммарное количество затрат труда и капиталовложений, необходимых для обеспечения конечной продукции Y=(Y1, Y2, …, Yn):
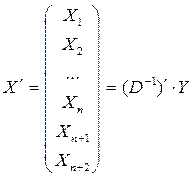 .
.
Пример. Дан межотраслевой баланс межотраслевой модели хозяйства
| № отрасли потребления | Конечный продукт | Валовый продукт | 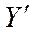
| ||||
| № отрасли производства | |||||||
Определить:
1) технологическую матрицу;
2) матрицу коэффициентов полных затрат;
3) матрицу коэффициентов косвенных затрат;
4) определить валовый выпуск 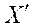 на новый ассортимент конечной продукции
на новый ассортимент конечной продукции 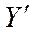 .
.
5) дать экономический анализ каждого столбца матрицы коэффициентов полных затрат;
Решение.
1)Находим коэффициенты прямых затрат: 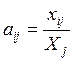
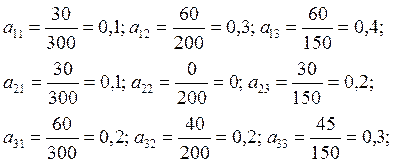
Матрица прямых затрат  имеет неотрицательные элементы
имеет неотрицательные элементы 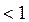 .
.
2) Найдем матрицу полных затрат.
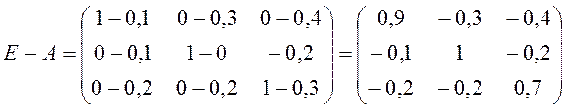
Вычислим 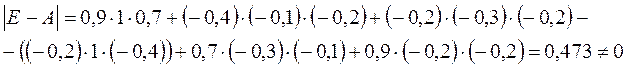
Обозначим E-A=D и вычислим алгебраические дополнения матрицы D.

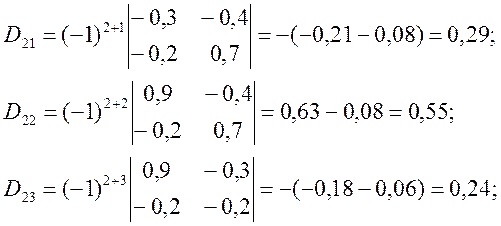
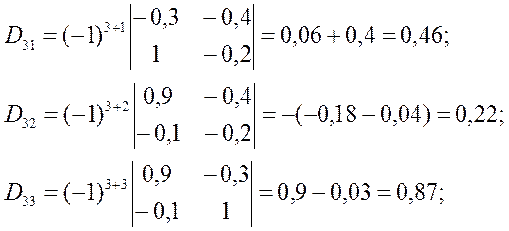
Присоединенная матрица:
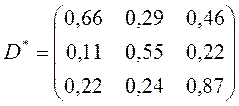
По формуле нахождения обратной матрицы:
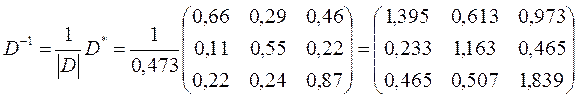 -матрица коэффициентов полных затрат.
-матрица коэффициентов полных затрат.
3) матрица коэффициентов косвенных затрат:

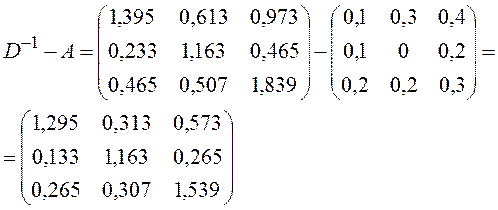
4) Найдем валовый выпуск на новый ассортимент конечной продукции по формуле: 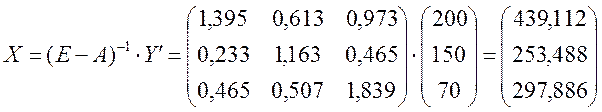 ,
,
т.е. валовой выпуск первой отрасли на новый ассортимент конечной продукции 439, 112 условных единиц, второй отрасли 253, 488 условных единиц, третьей отрасли 297, 886 условных единиц.
5. Экономический анализ
Столбец с номером j матрицы коэффициентов полных затрат означает какой необходим ассортимент (в валовом исчислении) производства продукции различных отраслей для производства одной единицы конечного продукта j-ой отрасли.
Первый столбец означает, что для того, чтобы получить для потребления одну единицу продукции предприятия 1-ой отрасли нужно произвести 1, 395 единиц продукции 1-ой отрасли, 0, 233 единиц продукции 2-ой отрасли, 0, 465 единиц продукции 3-ей отрасли.
Второй столбец означает, что для того, чтобы получить для потребления одну единицу продукции предприятия 2-ой отрасли нужно произвести 0, 613 единиц продукции 1-ой отрасли; 1, 163 единиц продукции 2-ой отрасли; 0, 507 единиц продукции 3-ей отрасли.
Третий столбец означает, что для того, чтобы получить для потребления одну единицу продукции предприятия 3-ой отрасли нужно произвести 0, 973 единиц продукции 1-ой отрасли, 0, 465 единиц продукции 2-ой отрасли, 1, 839 единиц продукции 3-ей отрасли.