Модель равновесных цен

Рассмотрим балансовую модель, двойственную к модели Леонтьева-модель равновесных цен.A-матрица прямых затрат, X- вектор валового выпуска.

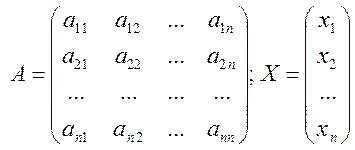
Обозначим через P вектор цен единицы продукции каждой отрасли:

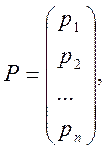где p_i-цена единицы продукции i-ой отрасли.

x_i- количество единиц продукции i-ой отрасли.

Тогда первая отрасль получит доход p₁x₁ , вторая – p₂x₂ и т.д.

Для выпуска единицы продукции 1-ой отрасли (x₁=1), ей необходима продукция 1-ой отрасли в объеме а₁₁, 2-ой отрасли - в объеме а₂₁, и т.д.

На закупку этой продукции 1-ой отраслью будет затрачена сумма:

a₁₁p₁+a₂₁p₂+…+a_n1p_n.

Следовательно, для выпуска продукции в объеме x₁ 1-ой отрасли необходимо потратить на закупку продукции других отраслей:

x₁(a₁₁p₁+a₂₁p₂+…+a_n1p_n).

Оставшуюся часть дохода, называемую добавленной стоимостью, обозначим через V₁ (эта часть дохода идет на выплату зарплаты и налогов, предпринимательскую прибыль и инвестиции). Таким образом, имеем равенство:

x₁(a₁₁p₁+a₂₁p₂+…+a_n1p_n)+V₁=x₁p₁.

Разделим левую и правую часть последнего равенства на x₁:

a₁₁p₁+a₂₁p₂+…+a_n1p_n+ v ₁=p₁, где 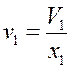–норма добавленной стоимости (величина добавленной стоимости на единицу выпускаемой продукции).

Подобным же образом получив уравнения для остальных n-1 отраслей, запишем систему:

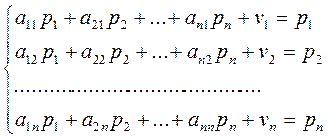(1)

Запишем систему (1) в матричной форме:

A^TP+v=P (2)

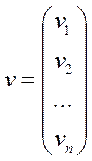- вектор норм добавленной стоимости.

Уравнение (2) называется моделью равновесных цен.

Как видим, полученные уравнения очень похожи на уравнения модели Леонтьева (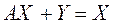) с той лишь разницей, что X заменен на P, Y - на v, A – на A^T.

Модель равновесных цен позволяет, зная величины норм добавленной стоимости, прогнозировать цены на продукции отраслей.

Уравнение (2) можно записать в виде:

P=D^Tv (3),

Где D^T=(E-A^T)^-1 – транспонированная матрица полных затрат.

Пример. Дана межотраслевая модель, состоящая из трех отраслей. Назовем их условно: топливно-энергетическая, промышленность и сельское хозяйство. Пусть известна транспонированная матрица прямых затрат:

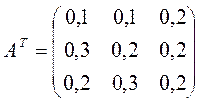. Вектор норм добавленной стоимости .

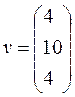Определить равновесные цены.

.

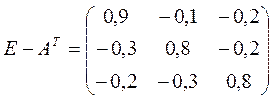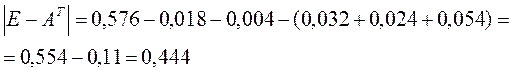
Найдем обратную матрицу:

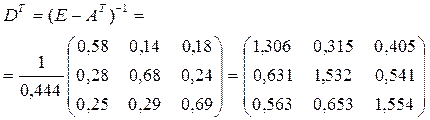
По формуле (3) найдем вектор P:

.

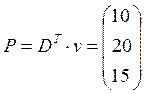Допустим теперь, что в топливно-энергетической отрасли произойдет увеличение нормы добавленной стоимости на 1, 11. Определим равновесные цены в этом случае. Принимая во внимание, что 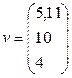, находим, что .

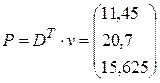Таким образом, продукция первой отрасли подорожала на 14, 5%, второй на- на 3, 5%, третьей отрасли- на 4, 17%.

10 – 100%

1, 45 – x%

x=(100*1, 45/10)=14, 5%.