
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейная модель множественной регрессии
|
|
В линейной множественной регрессии
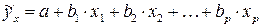 (1)
(1)
параметры при x называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего параметра на единицу при неизменном значении других факторов, закрепленных на среднем уровне.
Пример. Предположим, что зависимость расходов на продукты питания по совокупности семей характеризуется следующим уравнением:
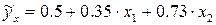 ,
,
где y – расходы семьи за месяц на продукты питания, тыс. руб.;
x 1 – месячный доход на одного члена семьи, тыс. руб.;
x 2 – размер семьи, человек.
Анализ данного уравнения позволяет сделать выводы – с ростом дохода на одного члена семьи на 1 тыс. руб. расходы на питание возрастут в среднем на 350 руб. при том же среднем размере семьи. Иными словами, 35% дополнительных семейных расходов тратится на питание. Увеличение размера семьи при тех же ее доходах предполагает дополнительный рост расходов на питание на 730 руб. Первый параметр не подлежит экономической интерпретации.
Классический подход к оцениванию параметров линейной модели основан на методе наименьших квадратов (МНК).
Этот метод позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака (y) от расчетных (теоретических) 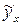 минимальна:
минимальна:
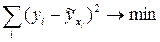 . (2)
. (2)
Чтобы найти минимум функции (2), надо вычислить производные по каждому из параметров и приравнять их к нулю, т.к. равенство нулю производной – необходимое условие экстремума. В результате получается система уравнений, решение которой и позволяет получить оценки параметров регрессии.
Так, для уравнения (1) система нормальных уравнений имеет вид:
 (3)
(3)
Решение системы (3) может быть осуществлено по одному из известных способов: Метод Гаусса, метод Крамера и т.д.
Пример. По четырем предприятиям региона (см. табл.) изучается зависимость выработки продукции на одного работника y (тыс. руб.) от ввода в действие новых основных фондов 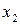 (% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих
(% от стоимости фондов на конец года) и от удельного веса рабочих высокой квалификации в общей численности рабочих 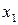 (%). Требуется написать уравнение множественной регрессии.
(%). Требуется написать уравнение множественной регрессии.
| Номер предприятия | ||||
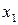 , (%) , (%)
| ||||
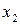 , (%) , (%)
| ||||
 , (тыс. руб.) , (тыс. руб.)
|