Седловая точка.

Седловая точка - это наибольший элемент столбца матрицы игры, который одновременно является наименьшим элементом соответствующей строки (в игре двух лиц с нулевой суммой). В этой точке, следовательно, максимин одного игрока равен минимаксу другого; С. т. есть точка равновесия.

Понятие седловой точки

Если в игре с матрицей А нижнее и верхнее, чистые цены игры совпадают т.е. 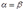, то говорят, что эта игра имеет седловую точку, в чистых выражениях и чистую цену игры:

Седловая точка — это пара чистых стратегий (i₀, j₀) первого и второго игрока, при котором достигается равенство .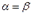

В понятии седловой точки вложен следующий смысл:

если один из игроков придерживается стратегии, соответствующей седловой точки, то другой игрок не может поступить лучше, чем придерживаться стратегии, соответствующей седловой точки.

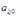— отклонение первого игрока от седловой точки может приводить только к уменьшению его выигрыша.

— отклонение второго игрока от седловой точки может приводить к увеличению его проигрыша .

Седловой элемент — является минимальным элементом строки и максимальным элементом в столбце.

Для определения седлового элемента необходимо последовательно в каждой точке определить минимальный элемент, а затем проверять является ли он максимальным элементом столбца и если является, тогда таким образом найдена седловая точка — цена игры, оптимальные стратегии первого и второго игрока:

14. Оптимальные стратегии.

В матричной игре каждый из игроков выбирает свои стратегии, не имея сведений о действиях другого игрока. Выясним, на какие наилучшие гарантированные выигрыши они могут рассчитывать. Первый игрок, выбрав некоторую стратегию i, может получить в качестве выигрыша один из двух элементов аi1, аi2 матрицы А в зависимости от того, какую стратегию применит второй игрок. В худшем случае он должен рассчитывать на минимальный выигрыш, т. е. на

.

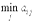В то же время при удачном выборе стратегии i = i* первый игрок может получить максимальный выигрыш из минимальных:

(5.2)

Второй игрок рассуждает сходным образом. При выборе стратегии j его максимальный проигрыш из двух возможных а1 j, а2 j равен

.

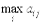Если выбор стратегии j = j* оказался удачным, то он может рассчитывать на минимальный проигрыш из максимальных:

. (5.3)

Формулы (5.2), (5.3) определяют наилучшие гарантированные выигрыши игроков. Если они совпадают, то их общее значение можно считать приемлемым для игроков компромиссом, а соответствующие стратегии i*, j* - оптимальными стратегиями.

Непосредственные вычисления по формулам (5.2), (5.3) с использованием (5.1) дают

Здесь наилучшие гарантированные выигрыши не равны и оптимальных стратегий не существует.

Причина отсутствия оптимальных стратегий кроется, очевидно, в их определении. Попробуем изменить определение оптимальных стратегий, не упуская из вида игрового смысла задачи и целей игроков.