Смешанные стратегии. Если в матричной игре отсутствует седловая точка в чистых стратегиях, то находят верхнюю и нижнюю цены игры

Если в матричной игре отсутствует седловая точка в чистых стратегиях, то находят верхнюю и нижнюю цены игры. Они показывают, что игрок 1 не получит выигрыша, превосходящего верхнюю цену игры, и что игроку 1 гарантирован выигрыш, не меньший нижней цены игры. В примере 2.3 игрок 1 получил по своей оптимальной стратегии А ₁, отличной от максиминной, выигрыш, равный верхней цене игры. Такова плата за информи­рованность о стратегии игрока 2. Это крайний случай. Не улуч­шится ли результат игрока 1, если информация о действиях противной стороны будет отсутствовать, но игрок будет много­кратно применять чистые стратегии случайным образом с опре­деленной вероятностью?

В такой ситуации, оказывается, можно получать выигрыши, в среднем большие нижней цены игры, но меньшие верхней.

Смешанная стратегия игрока - это полный набор примене­ния его чистых стратегий при многократном повторении игры в одних и тех же условиях с заданными вероятностями. Подведем итоги сказанного и перечислим условия применения смешанных стратегий:

• игра без седловой точки;

• игроки используют случайную смесь чистых стратегий с заданными вероятностями;

• игра многократно повторяется в сходных условиях;

• при каждом из ходов ни один игрок не информирован о выборе стратегии другим игроком;

• допускается осреднение результатов игр.

Применяются следующие обозначения смешанных стратегий.

Для игрока 1 смешанная стратегия, заключающаяся в применении чистых стратегий А₁, А₂,..., А_m с соответствующими вероятностями р₁, р₂,..., р_m,

где ,

Для игрока 2

где ,

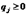
q_j – вероятность применения чистой стратегии В_j.

В случае, когда p_i = 1, для игрока 1 имеем чистую стратегию:

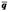Чистые стратегии игрока являются единственно возможны­ми несовместными событиями. В матричной игре, зная матрицу А (она относится и к игроку 1, и к игроку 2), можно определить при заданных векторах и средний выигрыш (математическое ожидание эффекта) игрока 1:

,

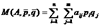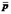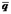где и - векторы;

р_i и q_j - компоненты векторов.

Путем применения своих смешанных стратегий игрок 1 стре­мится максимально увеличить свой средний выигрыш, а игрок 2 - довести этот эффект до минимально возможного значения. Игрок 1 стремится достигнуть

.

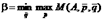Игрок 2 добивается того, чтобы выполнялось условие

.

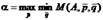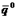Обозначим и векторы, соответствующие оптимальным смешанным стратегиям игроков 1 и 2, т.е. такие векторы и , при которых будет выполнено равенство

Цена игры  – средний выигрыш игрока 1 при использовании обоими игроками смешанных стратегий. Следовательно, реше­нием матричной игры являются:

1) - оптимальная смешанная стратегия игрока 1;

2) 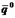- оптимальная смешанная стратегия игрока 2;

3)  - цена игры.

Смешанные стратегии будут оптимальными ( и ), если они образуют седловую точку для функции 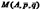, т.е.