
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы мезоскопического моделирования
|
|
Количественное исследование и предсказание эволюции микроструктуры материала, а также определение зависимостей “микроструктура материала – его физические свойства “ является, пожалуй, одной из наиболее активно разрабатываемых областей вычислительного материаловедения. Эволюция микроструктуры на микро- и мезо-уровнях, как правило, является термодинамически неравновесным процессом, в большой степени управляемым кинетикой процесса. Иными словами, “термодинамика” определяет основные направления развития микроструктуры, в то время как “кинетика” выбирает один из наиболее вероятных путей развития микроструктуры. Неравновесный характер эволюции микроструктуры приводит к необходимости учета большого числа различных типов дефектов решетки и взаимодействий.
Исследование микроструктурных особенностей на реальных временных и размерных шкалах, для предсказания макроскопических свойств материала, требует рассмотрения значительных объемов материала. Однако, вследствие того, что в этом случае мы вынуждены иметь дело с большим числом атомов (~1023 см-3), моделирование с использованием прямых решений уравнения Шредингера или с использованием других феноменологических атомистических подходов не представляется возможным. Поэтому, в большинстве случаев, для задач мезоскопического масштаба вводятся континуальные модели, в которых точные или приближенные решения уравнений движения всех атомов заменяются на усредненные соотношения и феноменологические кинетические уравнения. При этом, разнообразие мезоскопических процессов и их механизмов не позволяет, к сожалению, создать одного, универсального, метода построения мезоскопических моделей.
К настоящему моменту разработано огромное множество статистических, феноменологических и эмпирических моделей, как для случая пространственно не дискритизированного моделирования, так и для случая моделирования дискретного, как по пространству, так и по времени. В последнем случае, континуальная модель учитывает явным образом свойства дефектов решетки.
Последние пятьдесят лет, классические феноменологические мезоскопические модели, которые были дискретны по времени, но не по пространству, разрабатывались и использовались в применении к изучению вопросов пластичности кристаллов, явлений рекристаллизации, и фазовых переходов. Эти модели, как правило, обеспечивают скорее статистические, нежели дискретные решения, и могут быть использованы без применения трудоемких численных методов. Поэтому они часто используются, как основа для получения феноменологических уравнений, которые в дальнейшем могут быть использованы при моделировании, например, методом конечных элементов. Однако так как такое описание дает только некую усредненную картину отклика материала на изменение изменения внешних параметров, то оно ограничено только статистическими предсказаниями и не отражает особенности эволюции микроструктуры материала. Поэтому в последние годы, на первый план выходят методы, которые дискретны, как по пространству, так и по времени, и которые учитывают термодинамику и кинетику отдельных дефектов кристаллической структуры (Таблица 14.2). Таким образом, модели данного типа используют меньше феноменологических предположений, чем пространственно не дискритизированные модели и, как следствие, обладают большей предсказательной силой.
Таблица 14.2. Типы и области применения методов, обладающих свойством временной и пространственной дискретизации, класса мезо-уровня
| Модели моделирования, обладающие свойством временной и пространственной дискретизации, класса мезо-уровня | Область применения методов |
| Дислокационная динамика | Пластичность, текстуры, разрушение |
| Модели фазового поля или обобщенная модель Гинзбурга-Ландау | Диффузия, фазовые переходы, рост зерен |
| Детерминистические и стохастические методы клеточного автомата | Диффузия, теплопроводность, фазовые переходы, рекристаллизация, рост зерен |
| Кинетические многоуровневые модели Поттса | Фазовые переходы, рекристаллизация, рост зерен |
| Топологические и компонентные модели | Фазовые переходы, рекристаллизация, рост зерен |
| Модели топологических сетей и вершинные модели | Динамика границ, динамика сетей, зарождение, рост зерен |
Выделяют шесть основных групп методов, описывающих системы и протекающие в них процессы на мезо-уровне, а именно: пространственно-дискретизированную дислокационную динамику; обобщенную модель Гинзбурга-Ландау; детерминистические и стохастические методы клеточного автомата; кинетические многоуровневые модели Поттса; топологические и компонентные модели; модели топологических сетей и вершинные модели.
Все эти методы объединяет общее свойство, они не описывают динамику системы на атомных масштабах, а рассматривают систему как континуум. Это означает, что в рамках мезоскопических моделей дефекты кристаллической решетки рассматриваются, как объекты, инкорпорированные в некую гомогенную матричную среду, посредством которой и осуществляется их взаимодействие. Соответствующие уравнения таких математических моделей обычно не вводят явным образом внутренних пространственных или временных масштабов. Классификация этих подходов, как методов моделирования микро-или мезо-уровня в каком то смысле условна и зависит от конкретной используемой в подходе физической модели. Континуальные мезоскопические модели, включающие в себя учет дефектов кристаллической решетки, обычно используют набор феноменологических частичных дифференциальных кинетических уравнений и уравнений состояния. Вид этих дифференциальных уравнений, их коэффициенты и переменные отражают соответствующие временные и пространственные характеристики изучаемой системы, а также уровень дискретизации, характерный для метода, используемого для решения этих уравнений (метод конечных элементов, метод Монте-Карло и т.п.). Переменные в этих моделях, относящиеся к состоянию системы (например, атомные концентрации, плотность дислокаций, различные структурные параметры, смещения, или ориентация решетки) обычно описываются координатами пространственной сетки. Применяемые же к ним дифференциальные уравнения определяются характером взаимодействия (коротко-действующий или дальнодействующий). Так, модели Поттса, клеточного автомата и различные топологические подходы активно используются для моделирования различных поверхностей раздела, описывающихся коротко-действующими взаимодействиями. Модели же дискретной дислокационной динамики разработаны для моделирования линейных дефектов и, поэтому, рассматривают дальнодействующие взаимодействия.
Пространственно-дискретизованное моделирование дислокаций предполагает рассмотрение идеализированной дислокации без учета структуры ее ядра. В этой модели дислокация - некий линейный дефект, погруженный в гомогенную, изотропную или анизотропную, линейную упругую среду. Такая модель применима, как для случая прямых бесконечных дислокаций, так и для моделирования сегментов дислокаций. Моделирование в этом случае основано на дискретном моделировании динамики отдельных дислокаций, в котором время и положение каждого дефекта рассматриваются как независимые переменные. Динамика дислокаций, как правило, описывается исходя из предположений феноменологических законов вязкости для каждой дислокации или на основании второго закона Ньютона для дислокационного сегмента. Временная эволюция положений дислокаций определяется с использованием алгоритмов конечных разностей.
Модели кинетического фазового поля типа Гинзбурга-Ландау и Кана-Хилларда представляют собой группу общих и очень гибких феноменологических континуальных подходов, которые позволяют описывать явления непрерывного и квази-непрерывного фазового разделения в когерентных и некогерентных системах на наноскопическом и мезоскопическом уровнях. Оригинальная версия подхода Гинзбурга-Ландау была разработана для решения проблем электромагнетизма с неконсервативными полевыми переменными – определения концентрационного распределения куперовских пар. Однако данный подход также может использоваться для нахождения параметров непрерывно сохраняющегося распределения атомных концентраций и не сохраняющихся квази-непрерывных структурных и/или ориентационных параметров в когерентных и некогерентных системах. Подходы фазового поля, как правило, основаны на предположении, что материал однороден, и что химическая составляющая функционала плотности свободной энергии может быть выражена в форме Ландау. В тех версиях, в которых рассматриваются только консервативные полевые переменные (метод Кана-Хилларда), метод фазового поля ограничен только описанием изоструктурных фазовых переходов. В этом случае фазы могут отличаться друг от друга только концентрациями, но не дальним порядком и не кристаллической структурой.
Модели фазового поля могут рассматриваться как набор кинетических уравнений Онзангера, дополненные соответствующим функционалом свободной энергии, который может зависеть от таких величин, как атомные или бозонные концентрации и дальний порядок. Для перевода данного подхода в форму, дискретную по времени, указанные переменные рассматриваются, как переменные поля. Знание зависимости переменных от пространственных координат дает возможность описывать неоднородные системы и структурные поля, и позволяет моделировать кинетику выпадения фаз и их результирующую морфологию.
Идея клеточных автоматов появилась в конце сороковых годов XX в. Она была задумана и сформулирована Джоном фон Нейманом и Конрадом Цусе независимо друг от друга как универсальная вычислительная среда для построения, анализа и сравнения характеристик алгоритмов. В методе клеточных автоматов моделируемая среда рассматривается как ансамбль структурных элементов (клеточных автоматов) конечного размера, взаимодействующих по определенным правилам и законам. Клеточный автомат – это математический объект с дискретным пространством и временем. Пространство представляет собой поле, состоящее из набора клеток, образующих некоторую периодическую решетку. Время – последовательность шагов или поколений. Состояние каждой клетки определяется как функция от состояний клеток в некоторой её окрестности на предыдущем шаге. Эта функция одинакова для всех клеток поля. Таким образом, клеточный автомат представляет собой систему, поведение которой полностью определяется текущим состоянием поля и локальными взаимодействиями. Такая структура весьма удобна для моделирования различных физических, биологических и информационных процессов, особенно если среду нельзя рассматривать как непрерывную.
Применение клеточных автоматов позволяет получить сложное поведение без использования сложного и громоздкого математического описания. Различные методы клеточных автоматов активно применяются при решении широкого класса прикладных задач по описанию разнообразных процессов: физических, химических, биологических, гидродинамических и др.
Например, данный класс методов позволяет производить расчёт быстро протекающих динамических процессов таких, как распределение энергии в деформируемом твёрдом теле, не решая сложных дифференциальных уравнений, использование которых зачастую является весьма затруднительным.
Применительно к задачам, связанным с описанием процессов деформации и структурной перестройки твёрдых тел, методы клеточных автоматов оказались весьма эффективными. Так, с их помощью моделировались процессы рекристаллизации, деформационного упрочнения, пластической деформации, и т.д.
В настоящее время активно развивается метод подвижных клеточных автоматов. Данный метод применяется для решения задач компьютерного конструирования новых материалов, исследования закономерностей процесса разрушения хрупких материалов, исследования формирования динамических дефектов и их роли в процессе деформации и разрушения гетерогенных материалов и структур, изучения нелинейных эффектов в твёрдых телах при высокоэнергетическом воздействии, исследования закономерностей поведения геологических сред при динамических воздействиях, моделирования пластичного поведения образца на основе модификации функции отклика автоматов, и т.д. В целом, данный метод позволяет моделировать процесс растрескивания и множественную генерацию повреждений.
В применении к задачам материаловедения, элементы, составляющие моделируемую среду, характеризуются набором параметров, которые однозначно определяют его состояние. Этими параметрами могут быть, в частности, фазовый состав, температура, теплофизические и механические характеристики материала, составляющего клеточный автомат, параметры межавтоматного взаимодействия. При этом важной проблемой метода является выбор размера отдельного автомата di и установление правильного соответствия между свойствами элемента и его масштабом. Общего правила определения величины di, позволяющей корректно описывать процессы, происходящие на рассматриваемом масштабном уровне, не существует. Конкретный выбор di определяется условиями рассматриваемой задачи. Так, элементы могут составлять отдельные зёрна поликристалла, частицы порошковой смеси, фрагменты блоковых сред или структур и т.д. Отметим, что подобное представление моделируемой среды является общим для всех методов дискретного подхода в механике.
Принципиальным отличием метода подвижных клеточных автоматов от метода классических клеточных автоматов является введение предположения о возможности пространственного перемещения дискретных элементов среды за счет взаимодействия с соседями. Следствием способности автомата изменять свое пространственное положение является возможность смены окружения подвижных частиц в результате их перегруппировки. Поскольку в рамках метода клеточных автоматов всякое качественное изменение состояния системы должно реализовываться путем переключения состояния автоматов, для реализации новой способности в методе подвижных клеточных автоматов вводится новый тип состояний – «пространственное отношение пары элементов». Введение данного типа состояний можно рассматривать как расширение существующего в классическом подходе формализма, оперирующего состояниями отдельного автомата. В качестве основного параметра нового типа состояний рассматривается величина перекрытия пары элементов (hij), определяемая через изменение расстояния между центрами масс взаимодействующих автоматов по сравнению с равновесным расстоянием.
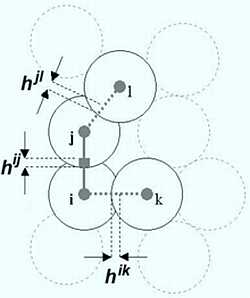
Рисунок 14.5 – Подвижные клеточные автоматы
Этот метод позволяет в явном виде описывать такие важные эффекты как разрушение, образование частиц износа, перемешивание материала, образование мостиков адгезионного схватывания, что даёт возможность моделировать поведение материала в динамике и детально исследовать механизмы эволюции структуры, отвечающие за те или иные закономерности контактного взаимодействия. Эволюция среды в этом случае описывается уравнениями трансляционного движения, учитывая силы, действующие между автоматами ij.

Здесь mi это масса автомата i, pij это сила, действующая между автоматами i и j, C(ij, ik) – коэффициент, ассоциированный с переносом параметра h из пары ij к ik, ψ (α ij, ik) - угол между направлениями ij и ik. Вращательные движения также могут быть учтены с точностью, определяемой размером клеточного автомата. Следует отметить, что уравнения полностью аналогичны уравнениям движения для много-частичной среды.
По своей сути модель Поттса – это обобщенная модель Изинга, для случая системы, состоящей из более, чем двух компонент (q > 2). Оригинальная Монте-Карло модель Поттса была разработана для нахождения некоторого физического параметра системы среднего по ансамблю на основе учета взаимодействия ближайших соседей. При этом, в Гамильтониане учитывается взаимодействие только “неподобных” соседей. В области материаловедения данная модель активно используется для моделирования таких процессов, как фазовые переходы, коалесценция, рекристаллизация и рост зерен.
Геометрические и компонентные модели в основном используются для моделирования процессов рекристаллизации и роста зерен в кристаллах. Как правило, моделирование с использованием данных моделей предполагает построение топологии типа Вигнера-Зейтца для некоторого начального распределения элементов пространственной решетки. Заданные элементы могут быть определены, как центры зарождения. Геометрические модели топологии роста не учитывают реальную динамику дефектов кристаллической решетки. Однако они дают возможность быстро получить предварительные предсказания для случая развития простых текстур в результате рекристаллизации и роста.
Методы топологических сетей и вершинные модели, в настоящее время, являются одними из наиболее широко распространенных подходов для моделирования динамики границ зерен, позволяя предсказывать как структурную эволюцию сети дислокаций, так и суб-зеренных и зеренных больше-угловых границ. В этих моделях границы зерен аппроксимируются прямыми или изогнутыми линейными дефектами. Линейные дефекты могут перераспределяться, следуя воздействию внешних полей, кривизне границы раздела, и градиентам внутренней энергии, накопленной границей, приводящим к росту сил, действующих перпендикулярно на каждый из элементов границы. В результате воздействия такой сети сил граница начинает смещаться. Как правило, такое движение описывается законами вязкого течения с использованием линеаризованных кинетических уравнений. Для получения решения уравнений используются схемы конечных разностей.