
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы Монте-Карло
|
|
Статистическая механика в атомистическом микроскопическом моделировании. Атомистическое и микроскопическое моделирование может использоваться для предсказания равновесных и переходных термодинамических состояний системы, корелляционных функций и динамики атомов. Это достигается посредством численных дискретных или статистических расчетов явлений многочастичного взаимодействия. Взаимодействие частиц обычно определяется соответствующим Гамильтонианом.
Зачастую, целью такого статистического атомистического моделирования является получить информацию, которую можно было бы экстраполировать на макроскопические масштабы. Это требует использования адекватных статистических методов. В данном разделе рассмотрим каким образом можно, используя, атомистические по своей природе методы, получить данные, относящиеся к макроскопическим масштабам.
Область статистической механики может быть разделена на два больших подраздела:
(1) равновесная статистическая механика – “ статистическая термодинамика ”, которая работает с законами равновесной термодинамики и рассчитывает величины термодинамических функций состояний и другие равновесные свойства систем на атомистических масштабах;
(2) неравновесная статистическая механика - “ статистическая кинетика ”, которая имеет дело с процессами достижения системами состояния термодинамического равновесия, выводом уравнений макроскопического транспорта и их коэффициентов, и другими неравновесными свойствами системы с точки зрения их атомистических свойств.
Микроскопическое термодинамическое состояние классического, то есть не квантового, атомного газа, содержащего N частиц, определяется тремя компонентами векторов позиций частиц, r1…rN, и тремя компонентами векторов их импульсов, p1…pN. Эти 6 N компонент, или степеней свободы, могут рассматриваться, как координаты в многомерном пространстве, который также называют многомерным фазовым пространством. В зависимости от предопределенных макроскопических параметров системы, то есть основной функции состояния, обычно выделяют фазовое пространство Гиббса и фазовое пространство Гельмгольца.
Указанные 6N компонент могут быть рассмотрены, как компоненты вектора Г( t ) в 6N- разрядном фазовом пространстве, где t описывает момент времени:
Г (t) = { r1 (t), …, rN (t), p1 (t), …, pN (t)}
Каждая точка фазового пространства представляет состояние системы в некоторый момент времени t. Если сравнивать метод молекулярной динамики, рассмотренный в 14.3.1.4 и метод Монте-Карло, то в качестве характерного различия может быть выделено следующее. В то время как моделирование МД позволяет проследить состояния системы вдоль некоторой детерминированной траектории, рассчитанной путем решения классических уравнений движения всех рассматриваемых частиц, моделирование Монте-Карло дает набор состояний вдоль стохастической траектории, рассчитанной путем существенной выборки (более подробно этот процесс будет рассмотрен ниже).
Таблица 14.2. Виды статистических ансамблей в моделировании Монте-Карло и молекулярной динамике.
| Статистический ансамбль | Обозначение | Предопределенные параметры | Характеристическая функция |
| микроканонический | NVE | число частиц (N), объем (V), энергия (E) | Энтропия S(N, V, E) |
| Канонический или макроканонический | NVT | число частиц (N), объем (V), температура (T) | Свободная энергия Гельмгольца F(N, V, T) |
| большой канонический | µVT | Объем (V), температура (T), химический потенциал (µ) | Функция Массье J(µ, V, T) |
| изобарически-изотермический | NPT | число частиц (N), давление (P), температура (T) | Свободная энергия Гиббса G(N, P, T) |
Детальный микроскопический анализ, включающий в себя координаты индивидуальных частиц, скорости, ориентаций и угловые скорости частиц/молекул, при изучении макроскопической картины системы, содержащей 1023 частиц, является практически невыполнимой задачей, да и не нужен. Для этого используются подходы статистической механики. Центральная идея статистической механики состоит в том, чтобы заменить 6 N микроскопических параметров, характеризующих термодинамическое состояние системы, несколькими макроскопическими параметрами, такими как: число частиц (N), объем (V), температура (T), энергия (E), химический потенциал (µ), и давление (P). В случаях, когда какие-то из макроскопических параметров системы предопределены (фиксированы), это может быть сделано путем расчета среднего значения флуктуирующих микроскопических параметров отдельных частиц.
Подобная процедура обоснована тем фактом, что число микро-состояний системы много больше числа макро-состояний. Иными словами, одно макро-состояние может быть реализовано набором множеств микро-состояний, то есть параметры частиц должны удовлетворять одним и тем же предопределенным макроскопическим параметрам, но при этом могут иметь различные микроскопические состояния. В этом случае, подобное усреднение, позволяет считать, что макроскопические свойства системы, состоящей из большого числа взаимодействующих частиц, не чувствительны к особенностям атомистического/микроскопического состояния.
Статистические данные могут быть получены из набора микроскопических параметров через их усреднение по времени или ансамблю. Эквивалентность этих типов усреднений следует из эргодической теоремы. Использование среднего по времени значения некоторой физической величины q, < q> time, отражает предположение, что экспериментально наблюдаемая макроскопическая величина < q> exp нечувствительна к временным флуктуациям микросостояний.
Соответственно, правомочность усреднения по ансамблю, < q> ens, основано на предположении, что макроскопически наблюдаемая величина < q> exp нечувствительна к флуктуациям фазового пространства микросостояний. Таким образом, усреднение по времени можно заменить усреднением по ансамблю, рассчитывая среднее по всем компонентам ансамбля в некоторый фиксированный момент времени t=tfix.
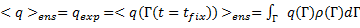 (14.36)
(14.36)
где ρ (Г) = ρ ( r1, …, rN, p1, …, pN ) – функция распределения вероятности, иногда также называемая функцией распределения фазового пространства или просто функцией распределения. Функция ρ (Г) пропорциональна вероятности, что для данного макросостояния в момент времени t=t0 система описывается микросостоянием, точка фазового пространства для которого лежит в пределах элементарного объема фазового пространства d Г в окрестности точки Г. Так как микросостояние обязано существовать где-то в фазовом пространстве, интеграл функции распределения по фазовому пространству должен быть равен 1:
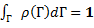 (14.37)
(14.37)
Функция плотности фазового пространства зависит от Гамильтониана системы:
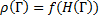 (14.38)
(14.38)
где Н(Г)=Еpot( r1, …, rN )+Ekin( p1, …, pN ) c Еpot( r1, …, rN ) обозначающим потенциальную энергию системы, и Ekin( p1, …, pN ) – кинетическую энергию.
Набор всех точек фазового пространства, в сочетании с относительной вероятностью их реализации, определяет ансамбль (Таблица 14.2). Иными словами, ансамбль характеризует вероятности всех разрешенных в пределах определенных макроскопических параметров микро-состояний. В области равновесной статистической механики рассматриваются стационарные ансамбли. В зависимости от набора фиксированных макроскопических параметров выделяют “макроканонический” или просто “канонический” ансамбль (фиксированы N, V, T), “микроканонический” (фиксированы N, V, E), “большой канонический” фиксированы (µ, V, T), и “изобарически-изотермический” (фиксированы N, P, T).
Макроканонический или канонический ансамбль часто используется в Монте-Карло моделировании, в котором N частиц находятся в ящике объема V, который в свою очередь находится в тепловом резервуаре (термостате) постоянной температуры T. В этом случае полная энергия системы и давление могут флуктуировать вокруг некоторого среднего значения. Характеристической функцией такого ансамбля является свободная энергия Гельмгольца F(N, V, T) (Таблица 14.2)
Функцию плотности фазового пространства, ρ NVT(Г), для случая канонического ансамбля удобно описывать, используя понятие вероятности, w(Г), обнаружить частицу с энергией Н(Г) и канонической статистической суммой ZNVT.
Основным предположением статистической механики является предположение, что все микросостояния системы с одинаковой энергией – равновероятны. В классическом каноническом описании вероятность может быть выражена через использование фактора Больцмана. Плотность вероятности wNVT (Г), которая описывает ненормализованный статистический вес, с которой конфигурация Г осуществляется в каноническом фазовом пространстве в условиях термического равновесия, может быть записана как:
 (14.39)
(14.39)
где 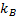 – константа Больцмана;
– константа Больцмана; 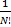 – фактор нормировки, который учитывает, что для N идентичных частиц перестановка индексов частиц не приводит к изменению состояния. Фактор
– фактор нормировки, который учитывает, что для N идентичных частиц перестановка индексов частиц не приводит к изменению состояния. Фактор 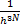 учитывает неопределенность Гейзенберга, где
учитывает неопределенность Гейзенберга, где  описывает величину наименьшего возможного объема фазового пространства, в котором могут быть одновременно определены вектора положений и импульсов.
описывает величину наименьшего возможного объема фазового пространства, в котором могут быть одновременно определены вектора положений и импульсов.
Каноническая статистическая сумма или статсумма (обозначается Z, от нем. Zustandssumme) - сумма по состояниям системы, ZNVT., которая интегрирует веса по всем возможным состояниям фазового пространства, играет роль нормировочного фактора:
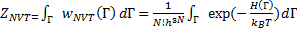 (14.40)
(14.40)
Каноническая функция плотности фазового пространства ρ NVT(Г) тогда может быть записана, как нормированная функция весового распределения
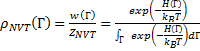 (14.41)
(14.41)
В случае дискретных значений энергий Н(Г) и неквантовых частиц, распределение которых подчиняется распределению Максвелла-Больцмана, удобно записать каноническую статсумму, как сумму, а не как интеграл:
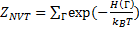 (14.42)
(14.42)
Тогда среднее значение некоторой физической величины по каноническому ансамблю может быть записано как
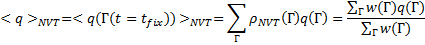
Микроканонический ансамбль представляет собой ансамбль с N частицами, находящихся в ящике объема V, и с фиксированной энергией E. Температура системы и давление могут флуктуировать вокруг некоторого среднего значения. Характеристической функцией такого ансамбля является энтропия S(N, V, E) (Таблица 14.2).
Для микроканонического ансамбля плотность вероятности wNVЕ (Г), которая описывает ненормированный статистический вес обнаружения конфигурации Г, в микроканоническом фазовом пространстве, записывается в следующем виде:
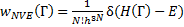 (14.43)
(14.43)
где Е – энергия системы и δ – дельта функция Дирака. Микроканоническая статсумма ZNVЕ имеет вид:
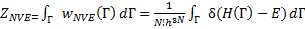 (14.44)
(14.44)
В случае дискретных значений энергий микроканоническая статсумма может быть записана как сумма:
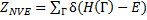 (14.45)
(14.45)
Большой канонический ансамбль с фиксированной температурой T, заданным химическим потенциалом µ, и фиксированным объемом V обычно используется в моделировании Монте-Карло. Энергия системы, давление, и число отдельных частиц могут флуктуировать около средних значений, как и в предыдущих случаях. Характеристической функцией такого ансамбля является функция Массье J(µ, V, T) (Таблица 14.2).
Плотность вероятности для большого канонического ансамбля имеет вид:
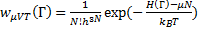 (14.46)
(14.46)
где µ - определенный химический потенциал, а N – число частиц. Статсумма для большого канонического ансамбля может быть выражена, как:
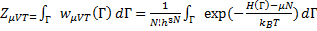 (14.47)
(14.47)
Аналогично случаям канонического и микроканонического ансамблей, если величина энергии принимает дискретные значения, то интегральная форма статсуммы может быть заменена выражением суммы:
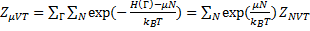 (14.48)
(14.48)
Следующим статистическим ансамблем, также активно используемым в моделировании методами Монте-Карло, является изобарически-изотермический ансамбль с заданными температурой T, давлением P и числом частиц N. В этом случае, около некоего среднего значения могут флуктуировать энергия системы и ее объем. Характеристической функцией такого ансамбля является свободная энергия Гиббса G(N, P, T) (Таблица 14.2).
Плотность вероятности для изобарически-изотермического ансамбля выражается как:
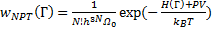 (14.49)
(14.49)
Где 𝛺 0 – постоянная объема, P – давление, и V – объем. В этом случае статсумма имеет следующий вид
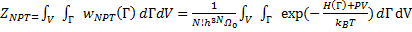 (14.50)
(14.50)
или, в случае дискретных значений энергии, в виде суммы:
 (14.51)
(14.51)
Статистическая сумма является фундаментальной величиной, позволяющей вычислять различные термодинамические функции в условиях термодинамического равновесия. Например, свободная энергия Гельмгольца, F, пропорциональна логарифму канонической статсуммы:
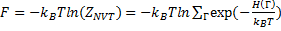 (14.52)
(14.52)
Свободная энергия Гиббса, G, пропорциональная логарифму статсуммы для изобарически-изотермического ансамбля:
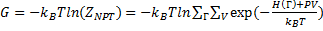 (14.53)
(14.53)
Используя эти две основные функции состояний можно получить и другие полезные термодинамические соотношения. Например, внутренняя энергия системы U может быть записана, как производная канонической статистической суммы:
 (14.54)
(14.54)
где 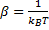 . Также можно записать выражения для энтропии S и давления P:
. Также можно записать выражения для энтропии S и давления P:
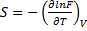 (14.55)
(14.55)
Метод Монте-Карло, применяемый в статистической физике, является частным случаем общего метода статистического моделирования, который используется для решения широкого круга задач в различных областях науки. Набор методик, обычно называемых Монте-Карло методами, включает в себя прямые подходы, имитирующие стохастические события, которые могут быть разбиты на отдельные процессы, и стохастические методы численного интегрирования многоразмерных определенных интегралов. Любая модель Монте-Карло характеризуется тремя процедурными составляющими: (1) исследуемая проблема определяется в понятиях вероятностной или статистической модели; (2) вероятностная модель разрешается путем численной стохастической выборки, и (3) полученные данные анализируются статистическими методами.
Вследствие активного использования в методе Монте-Карло стохастической выборки, его развитие было напрямую связано с развитием и совершенствованием вычислительных мощностей. Стохастический характер этого метода требует генерации большого числа некоррелированных случайных чисел. Применимость метода определяется центральной предельной теоремой теории вероятности.
В зависимости от распределения, из которого выбираются случайные числа, выделяют простую и существенную выборки. Более ранний класс выборки – простой, использует равномерное распределение случайных чисел. Более поздний класс выборок – существенный или выборка по важности (importance sampling), использует распределение, отражающее исследуемую проблему. Иными словами, суть существенной выборки заключается в том, чтобы выбирать большее количество случайных точек в существенных областях, то есть там, где подынтегральные функции принимают большие по модулю значения. Математическим основанием такого подхода служит тот факт, что плотность распределения случайных точек, доставляющая минимум функционалу дисперсии метода Монте-Карло, пропорциональна модулю подынтегральной функции. Такая плотность не может непосредственно использоваться в расчетах, поскольку поиск коэффициента пропорциональности не менее сложен, чем исходная задача. Однако, она может быть достаточно хорошо приближена, если имеется аппроксимация модуля подынтегральной функции, интеграл от которой легко вычисляется. Соответственно, для областей значений, для которых подынтегральные функции имеют малые значения, статистические веса – также малы.
Методы Монте-Карло, используемые в области материаловедения, могут быть сгруппированы по следующим группам:
(1) согласно используемому методу выборки: простая (невесовая) выборка, существенная (весовая) выборка. Процедуры простой выборки часто используются в перколяционных моделях, как невесовой стохастический метод интегрирования. Использование существенной выборки лежит в основе Монте-Карло алгоритмов, называемых алгоритмами Метрополиса;
(2) согласно типу рассматриваемой решетки – решеточное Монте-Карло: кубическая, гексагональная, решетка Воронова, и т.д.;
(3) согласно модели спинов – спиновое Монте-Карло: модель Изинга, модель Поттса, модель решеточного газа, модель Гейзенберга;
(4) согласно типу рассматриваемого оператора энергии: обменная энергия, упругая энергия, химический потенциал, магнитное поле, и т.д.
Общее описание алгоритма Монте-Карло, приводимое в любом руководстве по компьютерному моделированию, является чрезвычайно простым и в его классической версии может быть сведено к следующей последовательности повторяющихся шагов:
(i) выбрать событие (в некоторых версиях - несколько событий одновременно) среди всех событий, возможных в рассматриваемой системе;
(ii) согласно некоторому заранее определенному правилу определить вероятность того, что это событие произойдет.
(iii) принять решение - осуществить или отклонить осуществление рассматриваемого события.
(iv) обновить список возможных событий, принимая во внимание последствия последнего шага (если таковые имеются) и пересчитать их индивидуальные вероятности (если это требуется специфической реализацией алгоритма).
Практическое выполнение этой внешне простой схемы, однако, содержит так много деталей и «ноу-хау», что различные Mонте-Карло программы, моделирующие по существу один и тот же физический процесс, могут не иметь в алгоритмической реализации практически ничего общего, за исключением случайной природы выбора индивидуального события, что является краеугольным камнем Монте-Карло алгоритма.
Случайные числа. Как уже говорилось ранее, методы Монте-Карло могут быть использованы, как для моделирования много-частичных явлений, так и для интегрирования функций путем случайной выборки из серии некоррелированных случайных чисел, образующих Марковскую цепочку. Совершенно очевидно, что степень достоверности предсказаний метода зависит от “степени случайности” используемых чисел.
Согласно оригинальной идее, предложенной Метрополисом и фон Ньюманом, все генераторы псевдо-случайных чисел используют фиксированную длину слова цифрового компьютера. Позднее Лемер (1951) предложил метод, называемый конгруэнтным методом, в котором псевдо-случайная последовательность генерируется через операцию modulo, которая обрезает старт-стоповые биты большого целого числа, требующие больше компьютерной памяти, чем зарезервировано под длину слова. Математически это может быть выражено следующим образом:
(aR + c) modulo n → R
где R - случайное число, n – большое целое число, a – множитель цифр, которые не должны иметь никаких закономерностей, c – число, которое не должно иметь нетривиального фактора общего с n.
Алгоритм стартует с так называемого числа-“зерна” R0, величина которого может быть выбрана случайным образом. На каждом следующем шаге R умножается на a, которое выбирается согласно следующим трем правилам: (1) если n является степенью 2, то есть используется бинарная схема, то a выбирается таким образом, что a modulo 8 = 5; (2) a должно быть выбрано в интервале значений 0.01 n и 0.99 n; (3) значения а не должны следовать простой регулярной зависимости. Следующим шагом к произведению aR добавляется число c, которое не должно иметь общих значений с n.
Генераторы случайных чисел обычно идут в поставке библиотек к программным продуктам. Эти алгоритмы, основанные, как правило, на методах описанных выше, генерируют набор случайных чисел, который равномерно распределен в интервале значений (0, 1). Большинство алгоритмов генерации случайных чисел привязаны к конкретному языку программирования и конкретной вычислительной платформе (главным образом в части работы с целыми числами, обработкой переполнений и т.д.).
Набор случайных чисел, полученный с использованием компьютерных программных продуктов, не может быть истинно случайным, так как пути, которыми он создается, полностью детерминированы. Стохастические элементы моделируются путем использования алгоритмов, генерирующих последовательности большой периодичности. Поэтому, случайные числа, полученные при помощи компьютерных алгоритмов, называются псевдослучайными. Периодичность большинства псевдо-случайных последовательностей, полученных на 32-х разрядных компьютерах – порядка n, т.е. 2. Это вполне достаточное условие для большинства приложений, поскольку ошибка моделирования Монте-Карло уменьшается пропорционально n-1/2, где n – число случайных попыток.
Модель Метрополиса. В задачах статистической механики выражения «метод Монте-Карло» и «метод выборки Метрополиса» — почти синонимы. Модель Метрополиса является весовым алгоритмом, т.е алгоритмом, использующим для генерации состояний некоторого статистического ансамбля метод существенной случайной выборки для данного конкретного статистического ансамбля, который в случае термического равновесия характеризуется определенным предельным распределением вероятностей. Метод существенной выборки применительно к методу Монте-Карло упоминается в научных статьях уже в 1953 г. В этом методе есть несколько интересных сторон, присущих всем весовым методам. Во-первых, машинное время тратится в основном на расчет тех членов, которые внесут наиболее существенный вклад в сумму. Во-вторых, по сравнению с обычным методом Монте-Карло вычисления определенного интеграла, в сумму введены веса для учета «предвзятого» разыгрывания случайной величины.
Как уже обсуждалось ранее, термодинамическое состояние системы, состоящей из N классических частиц, может быть полностью определено тремя компонентами векторов позиций частиц, r1…rN, и тремя компонентами векторов их импульсов. Эти 6N компонент могут быть определены, как компоненты вектора Г в 6N- разрядном фазовом пространстве.
Два состояния ансамбля Гi и Гj связаны между собой вероятностью перехода pij – вероятностью, что система перейдет из состояния i в состояние j. Определим величину функции плотности вероятности для i -го состояния, как ρ (Гi), а j -го состояния, как ρ (Гj), а матрицу перехода i→ j, как pij. Для расчета компонент матрицы перехода Метрополис предложил следующее решение:
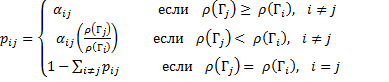 (14.56)
(14.56)
где α - симметричная и стохастическая матрица марковской цепочки. Как следует из записанной выше формы матрицы вероятностей, для случая, когда ρ (Гj)< ρ (Гi), для реализации алгоритма Метрополиса требуется только знание отношения ρ (Гj)/ ρ (Гi) и нет необходимости в знании статсуммы ансамбля ZNVT. При этом,
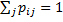 и
и 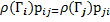 (14.57)
(14.57)
Первое уравнение отражает тот факт, что любое состояние Г i должно существовать где-то в фазовом пространстве. А второе уравнение указывает на принцип микроскопической обратимости. Это может быть использовано, в частности, для того чтобы продемонстрировать, что предельное распределение марковской цепочки есть функция распределения плотности вероятности.
Алгоритм Метрополиса основан на идее выбора случайным образом или систематически нового “пробного” состояния системы Гj, производя выборку из стохастической матрицы согласно
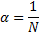
где N – число возможных положений частиц. После чего производится оценка изменения конфигурационной энергии системы в результате перехода системы из состояния i в состояние j, согласно отношению ρ (Гj)/ ρ (Гi).
Для этого, в подходе Метрополиса каждому из N атомов ансамбля приписывается некое начальное положение. После чего для полученной конфигурации рассчитывается значение Гамильтониана. Дальнейшая перестройка созданной начальной конфигурации системы зависит от предопределенных макроскопических величин. В канонической и микроканонической системах предопределяется число ее элементарных составляющих.
В моделях Монте-Карло с изменяющимися положениями частиц каждая последующая новая конфигурация создается путем случайного или систематического выбора одного из атомов, расположенного в позиции i и его последующего перемещения в новую пробную позицию j. Этот переход соответствует переходу системы из точки (Гi) в точку (Гj) фазового пространства. В результате такого перемещения система изменит энергию с Н (Гi) на Н (Гj). Отметим, что такое случайное смещение атома не приводит к изменению состава системы.
Такое перемещение принимается с определенной вероятностью. В каноническом и микроканоническом ансамблях рассчитывается изменение Гамильтониана системы, ∆ Н (Гi→ j)= Н (Гj)- Н (Гi), связанное с переходом системы в новую конфигурацию:
(1) если величина энергии новой конфигурации меньше, чем энергия предыдущей конфигурации, то такое смещение будет приводить систему в состояние с меньшей энергией. Поэтому такой переход немедленно принимается, и смещенная частица остается в своем новом положении.
(2) если величина энергии больше, чем на предыдущем шаге, то смещение принимается только с определенной вероятностью ρ (Гj)/ ρ (Гi), которая в случае канонической системы описывается фактором Больцмана:
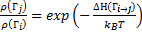 (14.58)
(14.58)
Таким образом, вероятность принятия изменения конфигурации для положительного изменения Гамильтониана пропорционально:
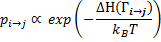
Следующим шагом в схеме Метрополиса выбирается случайное число, ξ, из интервала значений (0, 1): если выбранное случайное число ξ ≤ pi→ j, то событие принимается и система переводится в состояние с новой конфигурацией. В противном случае, событие отклоняется. Если новая конфигурация отклонена, система возвращается в предыдущее состояние, и вся процедура со случайным выбором атома и его смещением повторяется.
В большом каноническом ансамбле концентрация элементарных составляющих системы не фиксирована. Новая конфигурация системы j создается путем случайного выбора одного из атомов системы и предполагается, что он обменивается местами с атомом другого типа. Это процедура, в отличие от рассмотренного выше случая канонического и микроканонического ансамблей, влияет на изменения химического состава системы.
Аналогично процедуре, описанной выше, изменение конфигурации принимается с определенной вероятностью. В случае большого канонического ансамбля рассчитывается изменение энергии ∆ U (Гi→ j), связанное с изменением состава. Принятие новой конфигурации оценивается согласно следующему критерию: если значение величины энергии новой конфигурации меньше, чем предыдущей, то изменение конфигурации принимается. Однако, если величина энергии новой конфигурации больше, то изменения принимаются с определенной вероятностью. Вероятность принятия композиционного изменения в большом каноническом ансамбле для положительной величины ∆ U (Гi→ j) имеет вид
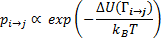
где ∆ U - изменение суммы энергий смешения и химического потенциала смеси. Если новая конфигурация отклонена, система возвращается в исходное состояние, и процесс выбора нового атома и изменения состояния системы повторяется.
Схема Метрополиса выбора событий в моделировании Монте-Карло является базовой и используется практически во всех широко используемых моделях Монте-Карло.
Модель Изинга является одной из простейших и основополагающих спиновых моделей. Данная модель относится к широкому классу решеточных моделей, в которых внутренняя энергия системы рассчитывается, как сумма парных взаимодействий спинов частиц, расположенных в узлах регулярной решетки. Изменение энергии в спиновой модели есть результат переориентации спина, а не смещения частицы из ее положения и/или обмена частицами их позициями в решетке. Спины в данной модели представляют собой магнитные моменты атомов в твердом теле, взаимодействующие друг с другом и внешним магнитным полем. Это, несомненно, является частным случаем и приемлемо для моделирования исключительно магнитных систем, и отражает тот факт, что оригинальная модель Изинга разрабатывалась специально для моделирования ферромагнитного упорядочения в веществах или бинарных сплавах. В отличие от модели Изинга, в модели Поттса, также представляющей класс спиновых моделей, спины могут представлять более-менее случайные свойства твердого тела. Модель Поттса иногда называется обобщенной или много-спиновой моделью Изинга. Моделирование с использованием спиновой модели Потта, как правило, относится к моделированию мезоскопического уровня.
Характерной особенностью классической модели Изинга является то, что она ограничена рассмотрением взаимодействия ближайших соседей. Однако, существуют также модели, разработанные на основе модели Изинга, которые учитывают взаимодействия и более дальнего порядка. Такие модели называются расширенными моделями Изинга. Дополнительным упрощением, положенным в основу классической модели Изинга, является то, что кинетическая энергия узлов решетки принимается равной нулю.
Итак, рассмотрим решетку, состоящую из N узлов. Свяжем с каждым i -ым узлом решетки число s = ± 1, характеризующее направление магнитного момента атома. Данная картина характерна для частиц с полуцелым спином. В классическом варианте модели Изинга спины рассматриваются, как классические степени свободы и, используемые в квантовой механике, правила коммутации углового момента не вводятся. Однако, расширенная модель Изинга, которая использует квантовый подход, также существует и называется моделью Гейзенберга.
Любое микросостояние решетки задается набором переменных { s 1, s 2, …, sN }. Учитывая, что макроскопические свойства системы определяются свойствами достигаемых ею микросостояний, зависимость полной энергии системы, E, от конфигурации спинов при наличии магнитного поля В в классической модели Изинга записывается как:
 , si =±1 (14.59)
, si =±1 (14.59)
где < i, j > означает, что сумма берется по всем ближайшим соседним парам спинов, константа обменной связи, J, характеризует силу взаимодействия соседних спинов.
В случае J > 0 (уравнение 14.59), для системы реализуется состояние с преимущественной ориентацией спинов -  и
и  (т.е. одинаковая ориентации спинов ближайших соседей), которое энергетически более выгодно, чем состояние, в котором спины соседних атомов ориентированы в противоположных направлениях -
(т.е. одинаковая ориентации спинов ближайших соседей), которое энергетически более выгодно, чем состояние, в котором спины соседних атомов ориентированы в противоположных направлениях -  и
и  . Это означает, что для J > 0 состояние с наименьшей полной энергией является ферромагнитным. Если J < 0, то с энергетической точки зрения более предпочтительными оказываются состояния
. Это означает, что для J > 0 состояние с наименьшей полной энергией является ферромагнитным. Если J < 0, то с энергетической точки зрения более предпочтительными оказываются состояния  ,
,  , для которых соседние спины антипараллельны. Следовательно, среднее число спинов, сориентированных в одном направлении, равно нулю - антиферромагнитное состояние.
, для которых соседние спины антипараллельны. Следовательно, среднее число спинов, сориентированных в одном направлении, равно нулю - антиферромагнитное состояние.
При наложении внешнего магнитного поля, B (уравнение 14.59), спины  и
и  приобретают дополнительную внутреннюю энергию, равную ± В где знак зависит от ориентации спина по отношению к вектору приложенного магнитного поля.
приобретают дополнительную внутреннюю энергию, равную ± В где знак зависит от ориентации спина по отношению к вектору приложенного магнитного поля.
Далее примерный алгоритм моделирования двумерной системы, состоящей из N спинов, методом Монте-Карло может состоять из следующей последовательности действий.
1. Задание числа спинов решетки N спин.
2. Задание числа шагов метода Монте-Карло на спин.
3. Задание ориентации спинов в узлах решетки в момент времени t = 0 (начальной конфигурации системы).
Все возможные конфигурации системы определяются заданием значений всех спиновых переменных, число которых составляет 2 N, а вклад любой из 2 N спиновых конфигураций определяется функцией распределения для канонического ансамбля.
4. Выбор случайным образом одного из спинов системы и изменение его ориентации.
5. Вычисление изменения энергии, ∆ E, в результате изменения ориентации спина согласно уравнению 14.59.
6. Если энергия новой конфигурации меньше, чем энергия предыдущего состояния системы, то событие принимается. Если же ∆ E > 0, то есть перевод системы в новое состояние сопровождается повышением энергии, то разыгрывается следующая вероятностная процедура подобная процедуре Метрополиса.
6а. Для этого рассчитывается вероятность, p, реализации такого события, приводящего к изменению энергии, ∆ E:
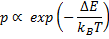
6б. Генерируем некое случайное число, 0< ξ < 1. Если рассчитанная вероятность p ≤ ξ, то такое событие принимается. В противном случае, событие – отклоняется.
9. Повторение пп. 4-8 (число повторений равно числу спинов в системе).
10. Повторение пп. 4-9 (число повторений равно числу шагов метода Монте-Карлона спин).
Таким образом, в результате выполнения алгоритмической процедуры можно проследить эволюцию спинового распределения в системе и определить статистически среднее распределение и значение магнитного момента системы для данных конкретных условий вычислительного эксперимента, как то: величина магнитного поля и, возможно, температура.
Заметим, что в модели Изинга спины должны выбираться случайно, что позволит избежать множественного учета периодически повторяющихся конфигураций. Следует также учесть граничные условия. В качестве таковых целесообразно выбрать периодические (тороидальные в двумерном случае) граничные условия, что обеспечит равное число взаимодействий для всех спинов в изучаемой системе.
Здесь же упомянем другие спиновые модели, имеющие прямое отношение к области моделирования свойств материалов. Кроме уже упомянутых выше моделей Потта и Гейзенберга, также используются модели решеточного газа и модели приближения молекулярного поля, кластерный вариационный метод и модель Брэгга-Вильямса-Горски. Все эти модели объединяет общая особенность: эволюционные и термодинамические свойства моделируются с использованием переориентации спина частицы, в некотором случайном узле регулярной решетки, с последующим определением взвешенного значения изменения энергии с использованием подхода выборки Метрополиса.
Метод Кинетического Монте-Карло. Для того, чтобы в кристаллах с дефектами исследовать кинетические эффекты на масштабах длин, намного превышающих достижимые в рамках расчетов методом теории функционала плотности, необходимо применять альтернативные методы моделирования. Двумя самыми широко распространенными подходами, имеющими дело с ячейками, содержащими миллионы атомов, являются молекулярная динамика и кинетическое Монте-Карло. Выбор между этими методами обычно делается, исходя из временной шкалы, характерной для рассматриваемых процессов, протекающих в кристаллах. Для исследования кинетики диффузии дефектов и их кластеризации при различных температурах кристалла и уровнях его легирования наиболее адекватным вычислительным инструментом является решеточное кинетическое Монте-Карло (РКМК). Использование для определения вероятности диффузионных переходов набора параметров (таких как энергии образования дефектов, их связи между собой, барьеров миграции и т.д.), полученных из первопринципных расчетов, гарантирует высокую надежность предсказаний РКМК.
Массоперенос в твердых телах происходит обычно как последовательность индивидуальных событий - диффузионных скачков, которые могут, в общем случае, описываться как обмен положениями пар атомов или точечных дефектов в решетке. Достаточно часто (например, при исследовании диффузии примесей замещения по вакансионному механизму) встречается ситуация, когда одна частица является собственным точечным дефектом, в то время как другая – реальным атомом (решеточным или примесным). Индивидуальные скачки происходят беспорядочно и их вероятности в единицу времени (частоты), pi, зависят от природы обменивающихся частиц, расстояния между ними и, как правило, химического состава окружающей их среды. Обычно перескакивающая частица имеет выбор между несколькими возможностями скачка, и никогда нельзя сказать заранее, какое конкретное событие, из имеющих ненулевую частоту, произойдет в заданном временном интервале. Иными словами, стартуя с любой фиксированной начальной конфигурации диффундирующих частиц в кристалле, можно представить множество существенно различных последовательностей скачков и, следовательно, не имеет большого смысла отслеживать эволюцию каждой отдельной частицы. Решеточное кинетическое Монте-Карло как раз и предназначено для " макроскопического" описания ансамбля диффундирующих частиц например, когда основной интерес представляет статистика образования различных кластеров за определенное время, которая сравнительно слабо чувствительна к подробностям кинетического поведения отдельных частиц при образовании кластеров.
В стандартном численном РКМК эксперименте рассматривается небольшая часть соответствующей кристаллической решетки с некоторой начальной конфигурацией распределения атомов примеси и точечных дефектов. Если задан алгоритм, позволяющий определять частоты скачков подвижных частиц в любом конкретном локальном химическом окружении, то метод позволяет прослеживать кинетику ансамбля дефектов и примесей, последовательно выбирая достаточно маленькие временные интервалы и позволяя подвижным дефектам перескакивать в соседние узлы решетки с вероятностями, соответствующими текущей конфигурации дефекта. В результате последовательного проведения такого вычислительного алгоритма получается некоторая конкретная реализация чисто стохастического процесса движения дефектов и их взаимодействия между собой. Однако в случаях, когда либо число частиц в ячейке моделирования, либо число прогонов программы с подобными начальными условиями являются достаточно большими, моделирование обеспечивает репрезентативную качественную картину " средних" тенденций развития ансамбля дефектов.
Очевидно, для того чтобы разумно представить кинетику реальных систем, даже ограничиваясь грубым " средним" поведением, вычислительный Монте-Карло эксперимент должен удовлетворять определенным требованиям, которые могут быть грубо разделены на две категории, а именно, – адекватности определения вероятностей всех диффузионных скачков перед каждым MК шагом и адекватности алгоритма движения частицы (осуществления собственно MК шага). Для обоих аспектов MК моделирования в литературе предложены различные алгоритмические решения, как правило учитывающие специфику моделируемых систем. Однако, независимо от конкретного вида алгоритмов, разумное описание конкретных атомных систем требует использования зависимых от системы параметров, которые являются для программы внешними (входными) данными. Поскольку, как правило, результаты MК моделирования весьма чувствительны к значениям используемых параметров, адекватность входных данных является существенным фактором надежности предсказаний численного эксперимента.
Основные события. Различия в МК кодах возникают уже на самом первом шаге, связанном с выбором того, что рассматривать в качестве основных событий для конкретной моделируемой системы. Оставаясь в рамках проблемы отжига и кластеризации дефектов и атомов примеси в твердом теле, можно рассматривать в качестве индивидуальных все различные объекты, встречаемые в системе, включая изолированные дефекты, атомы примеси, комплексы разных размеров и конфигураций, см. рис. 14.4(а). В этом случае нетривиальное событие можно определить, как преобразование одного или нескольких объектов в некоторые другие объекты. Например, когда два объекта типа " моновакансия" оказываются на расстоянии ближе некоторого предельного, они преобразуются в новый объект " дивакансия" со свойствами (подвижность, тепловая стабильность, вероятность захвата на других объектах, и т.д.), характерными для этого специфического типа объекта и не имеющими, вообще говоря, ничего общего со свойствами тех объектов (в данном конкретном случае - моновакансий), из которых он реально состоит. Этот подход обычно называется " объектное Монте-Карло ".
С другой стороны, можно не забывать, что кристаллические твердые тела состоят из атомов, занимающих узлы решетки, и вероятность события типа «диффузионный перескок» может быть определена для любого атома и точечного дефекта в зависимости от его положения и локального химического окружения. При этом кластеры дефектов рассматриваются как совокупность составляющих их атомов или точечных дефектов, рис. 14.4(б). Последний подход носит называние " решеточного" или " атомистического" Монте-Карло.
Отметим, что оба подхода имеют как сильные, так и слабые стороны, и в практических расчетах являются скорее дополняющими, чем конкурирующими. Однако, полностью различная природа элементарных событий в этих подходах подразумевает существенные различия и в алгоритмической реализации, и в основных наборах специфических для данной системы входных параметров, даже если речь идет об одной и той же физической системе.

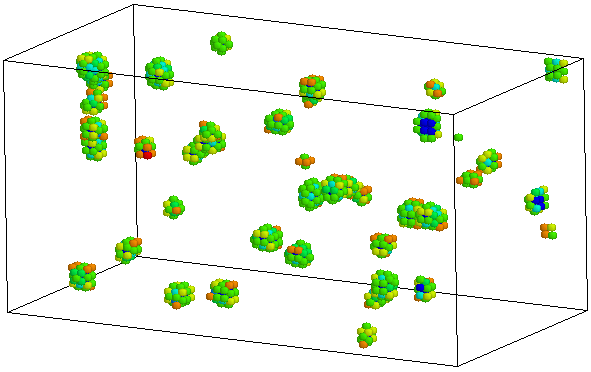
(а) (б)
Рис. 14.4. Соотношение между объектным (а) и решеточным (б) методами Монте-Карло. Один и тот же набор кластеров в первом случае представлен как совокупность индивидуальных объектов, во втором – как совокупность индивидуальных атомов различного типа.
Кинетическое поведение системы. Значительные различия между MК кодами могут быть связаны и с конкретной реализацией " вероятностного" шага алгоритма. Один из аспектов этих различий связан с выбором критериев принятия/отбрасывания события, который диктуется целью моделирования. Во многих приложениях цель моделирования состоит в том, чтобы как можно быстрее найти требуемое (например - наиболее энергетически выгодное) конечное состояние, независимо от того насколько физически разумны были промежуточные состояния системы во время расчета. В других случаях основной интерес представляет наиболее энергетически выгодное конечное состояние, которое в реальных системах может быть вообще недостижимо за разумные времена. Алгоритмы Монте-Карло, позволяющие воспроизводить физически осмысленные пути эволюции исследуемой системы, обычно называются " кинетическими".
В рамках " кинетических" алгоритмов конкретные программы различаются, в частности, " локальной" или " глобальной" природой используемого критерия принятия события. В классических схемах MК каждое последующее событие выбирается случайным образом из всех вообразимых событий, после чего вероятность совершения MК шага вычисляется " локально", только для данного конкретного события. Это делает алгоритм сравнительно простым в реализации и очень часто - исключительно быстрым, потому что расчет вероятности единичного события требует информации только об объектах в непосредственной близости от объекта, участвующего в событии. Однако, когда подавляющее число мыслимых событий имеет нулевую или очень низкую вероятность, эффективность такого алгоритма становится низка, потому что большинство отобранных событий не принимается. Альтернативный подход требует предварительного определения вероятностей всех событий, которые могут случиться на текущем шаге MК и выбор объекта для диффузионного скачка производится только из событий с ненулевой (или просто достаточно высокой) вероятностью. Это позволяет отказываться с самого начала от всех " пустых" событий, что частично компенсирует зачастую достаточно трудоемкий перерасчет вероятностей отдельных событий перед каждым MC шагом. Однако такой перерасчет дает очень важное преимущество перед алгоритмами, основанными на локальных критериях принятия событий, позволяя отслеживать развитие системы в зависимости от реального времени, а не просто от числа проделанных MК шагов.
Действительно, зная текущие частоты всех возможных событий, можно вычислить полную вероятность осуществления хотя бы одного (любого) события, p, как сумму всех текущих вероятностей событий, pi,
 . (14.60)
. (14.60)
Тогда среднее время D t требующееся для реализации одного события, отбираемого из всех возможных с учетом его индивидуального вклада в полную вероятность P, можно оценить как  . Этот временной интервал и выбирается в качестве длительности последующего шага МR. Алгоритмы, позволяющие отслеживать время эволюции моделируемой системы называются алгоритмами " непрерывного времени ".
. Этот временной интервал и выбирается в качестве длительности последующего шага МR. Алгоритмы, позволяющие отслеживать время эволюции моделируемой системы называются алгоритмами " непрерывного времени ".
Определение вероятностей событий. Согласно общей теории диффузии, частота pi для элементарного события i, представляющего собой диффузионный скачок, может быть выражена в форме закона Аррениуса,
fp= f0 exp (-(Esp - Ein)/kBT), (14.61)
где f0 - некая константа с размерностью обратного времени, Esp - энергия атомной системы в момент, когда обменивающиеся атомы находятся в конфигурации " седловой точки", Ein – энергия атомной системы перед скачком и kBT имеет его обычное значение произведения постоянной Больцмана на абсолютную температуру. Температура системы, как правило, может варьироваться в соответствии с рассматриваемой задачей, но входящие в формулу (14.61) энергетические параметры, являются свойствами моделируемой системы и должны быть определены вне программы КМК. Часто эти энергии зависят не только от того, какая пара частиц участвует в скачке, но и в каком окружении эти частицы находятся. Ближайшие соседи перескакивающих частиц, а иногда также вторые, третьи, и соседи большего порядка могут внести свой вклад в изменения энергии, связанные с диффузионными скачками. За исключением простейших модельных ситуаций, полное число возможных атомных конфигураций является настолько большим, что не представляется возможным точно задать всю совокупность возможных энергий физически различных диффузионных скачков, что приводит к необходимости использования различных упрощений.
На практике доступная для моделирования информация крайне ограничена и сводится к энергии образования индивидуальной диффундирующей частицы в решетке и энергии связи между парами частиц одного или различных типов. Энергии активации диффузии частиц известны надежно далеко не всегда, поскольку их расчеты и/или экспериментальные измерения крайне сложны. Для того, чтобы прийти к физически разумным результатам, приходится использовать интерполирование энергетических параметров, исходя зачастую из " минимального набора" данных.
Наиболее часто используемой моделью расчета энергий частиц в равновесных положениях на решетке является приближение " парных связей". Такой вид модели предполагает, что полная энергия кристалла E всегда может быть представлена как сумма вкладов от каждой пары атомов в кристалле,
 , (14.62)
, (14.62)
где N - полное число атомов в кристалле. Обычно предполагается, что вклад Eij от пары атомов зависит только от химической природы атомов этой пары и от расстояния между ними. Также предполагается, что взаимодействие уменьшается с увеличением расстояния, так что вклады от атомных пар, разделенных расстояниями свыше некоторого критического, - исчезающе малы. Удобство модели парных связей в том, что вклады Eij можно выразить через энергии связи пар частиц на бездефектной кристаллической решетке, что позволяет использовать для их расчета кватново-механические методы или полуэмпирические потенциалы.
Нередко оказывается, что для каких-то диффузионных скачков энергии седловой точки не известны. В этом случае приходится постулировать дополнительное приближение для энергии в положении седловой точки скачка, Esp. Наиболее часто используется представление вида
Esp = Em + max (Ein, Efi), (14.63)
где Efi - энергия системы после скачка и Em - барьер миграции. Такой выбор гарантирует, что отношение вероятностей перехода для прямого и обратного скачка удовлетворяет фундаментальному соотношению, известному как " принцип детального равновесия". В самом простом подходе, наиболее широко используемом в практике МС моделирования, зависимостью барьера миграции от окружения обменивающейся пары атомов пренебрегается и предполагается, что он соответствует барьеру для тех же самых частиц в идеальной кристаллической решетке матрицы. Следующим, более сложным приближением является учет вкладов в барьер миграции от атомов, являющихся ближайшими соседями от положения седловой точки диффузионного скачка для пары обменивающихся положениями частиц. Однако это возможно только при наличии соответствующей информации относительно энергий указанных вкладов.
Сама же процедура принятия или отклонения события в КМК проводится подобно описанной выше процедуре Метрополиса.