
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Типы элементов
|
|
Элемент типа С. Элемент типа С характеризует емкость, инертность и другие подобные свойства моделируемой системы. Графическое изображение такого элемента (двухполюсника) показано на рис. 2, а. Для механических подсистем используют также иное условное обозначение (рис. 2, б), при этом параметру С присваивают символ т.
Компонентное уравнение (1) для элемента типа С имеет вид
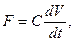 (4)
(4)
где F и V – соответствующие потоковые и потенциальные фазовые переменные.
В электрических подсистемах элемент типа С определяет электрическую емкость и описывается уравнением
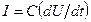 , (4a)
, (4a)
где I и U – соответственно сила тока и падение напряжения.
В механических подсистемах элемент С характеризует массу тела в уравнении второго закона Ньютона:
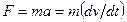 . (46)
. (46)
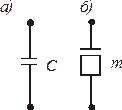
Рис. 2. Элемент типа С
Аналогично для механических вращательных подсистем формулу (4) можно записать в виде
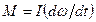 , (4в)
, (4в)
где М– момент силы; I – момент инерции; 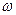 – угловая скорость.
– угловая скорость.
В тепловых подсистемах С характеризует теплоемкость тела C=dQ/dT, где dQ — изменение количества теплоты в теле при изменении температуры на dТ.
Компонентное уравнение (4) применительно к тепловому потоку Ф и температуре Т имеет вид
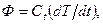 (4г)
(4г)
где 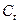 – теплоемкость тела, зависящая от удельной теплоемкости с и массы m тела:
– теплоемкость тела, зависящая от удельной теплоемкости с и массы m тела: 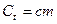 .
.
В гидравлических и пневматических подсистемах значения С характеризуют степень сжимаемости жидкости (газа) при плотности ρ и объеме V: C=pβ V. При этом связь между давлением ρ и расходом Qm определяется формулой
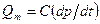 . (4д)
. (4д)
Аналогия уравнений типа (4) не является чисто формальной с точки зрения одинакового математического описания. Вероятно, за этой аналогией стоят скрытые закономерности, присущие природе в форме энергетических либо иных взаимных соответствий, тем более, что для всех рассмотренных подсистем между фазовыми переменными F и V существуют также аналогии для элементов типов L и R. Возвращаясь к элементу типа С, мы можем отметить, что С есть мера «емкости» или мера «инертности» при взаимодействии фазовых переменных в формах потока и потенциала, а точнее, при взаимосвязи потока со скоростью изменения потенциала. В механических подсистемах мерой инертности служит масса, в электрических и тепловых – емкость (теплоемкость). Изменение во времени потенциала (скорости движения в механических подсистемах, напряжения в электрической цепи, температуры при нагреве тела) приводит к изменению потока (движущей силы в механических системах, силы тока в электрических цепях, теплового потока при нагреве тел). Мерой взаимного соответствия этих изменений служит величина С. Чем больше емкость конденсатора, масса автомобиля, теплоемкость чайника с водой, тем труднее зарядить конденсатор до напряжения U, разогнать автомобиль до скорости v, нагреть воду до температуры Т.
Элемент типа L. Элемент типа L на эквивалентных схемах электрических и других подсистем изображают как катушку индуктивности (рис. 3, а). Для механических подсистем обычно используют условное обозначение пружины (рис. 3, б).
Компонентное уравнение для элемента типа L записывают в виде
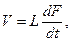 (5)
(5)
где V, F – потенциальная и потоковая фазовые переменные.
В электрических подсистемах элемент типа L определяет индуктивность, при этом напряжение U связано с силой тока I зависимостью
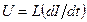 . (5 а)
. (5 а)
Для механических подсистем компонентное уравнение
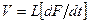 (5 6)
(5 6)
может быть получено путем дифференцирования по времени уравнения пружины F= kx, где х – перемещение; k – жесткость пружины. В формуле (5, б) аналог электрической индуктивности L характеризует податливость пружины 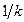 .
.
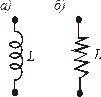
Рис. 3. Элемент типа L
Аналогичное компонентное уравнение можно получить для упругого стержня, используя закон Гука. При растяжении (сжатии) будем иметь
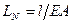 ; (5 в)
; (5 в)
при изгибе
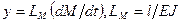 ; (5 г)
; (5 г)
при кручении
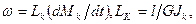 (5 д)
(5 д)
где Е, G – модули упругости при растяжении и сдвиге; А – площадь поперечного сечения; J, Jk – моменты инерции при изгибе и кручении.
В гидравлических и пневматических подсистемах давление р идеальной жидкости (газа) связано с массовым расходом Q уравнением
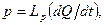 (5 е)
(5 е)
где Lp – l/A зависит от длины трубопровода l и площади его поперечного сечения А. Для реальных жидкостей формула (5е) не учитывает массовые силы и гидравлическое сопротивление, которые могут быть учтены дополнительно
Элемент типа R. Условное графическое изображение элемента типа R показано на рис. 4 для электрических (а) и механических (б) подсистем. Общее уравнение такого элемента имеет вид
F= V/R. (6)
В электрических подсистемах этому уравнению соответствует закон Ома
 ; (6 a)
; (6 a)
в механических — уравнение вязкого трения:
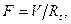 (6 б)
(6 б)
где 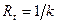 — величина, обратная коэффициенту вязкого трения;
— величина, обратная коэффициенту вязкого трения;
в гидравлических — отмеченное выше гидравлическое сопротивление:
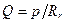 , (6 в)
, (6 в)
где 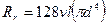 – аналог электрического сопротивления (v – кинематическая вязкость; d, l — диаметр и длина трубопровода);
– аналог электрического сопротивления (v – кинематическая вязкость; d, l — диаметр и длина трубопровода);
в тепловых подсистемах:
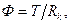 (6 г)
(6 г)
где тепловой поток Ф и температура Т зависят от конвекционного сопротивления Rk.
Таким образом, во всех рассмотренных подсистемах можно установить аналогии фазовых переменных типа потока и потенциала (табл. 1).
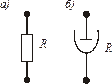
Рис. Элемент типа R
17.3 Источники энергии и преобразователи. Аналоги топологических уравнений
Условное графическое изображение источников энергии типа Е и I показано на рис. 5.
На рис.. 6, а приведена схема трансформатора, имеющего математическую модель
 (7)
(7)
где Т – коэффициент трансформации.
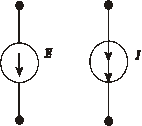
Рис. 5.Источники энергии
Примерами трансформаторов в механических подсистемах могут служить рычаги энергии и редукторы.
Гиратор (рис. 6, б) имеет модель
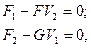 (8)
(8)
где G – коэффициент гирации.
Примером гиратора может служить гидроцилиндр, в котором давление Р преобразуется в силу F, действующую на поршень.
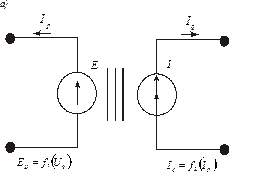
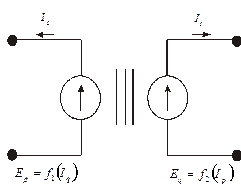
Рис. 6.Схемы трансформаторной (а) и гираторной (б) связи
Топологические уравнения типа (7), (8) в большинстве физических подсистем базируются на уравнениях равновесия и уравнениях неразрывности. Ниже рассмотрены аналогии топологических уравнений в подсистемах различной физической природы. Условимся снабжать индексом i элементы, примыкающие к данному узлу, а индексом j – входящие в данный контур, при этом в знаках суммы (∑)обозначения « » или «
» или «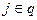 », где p, q – соответственно множество ветвей, примыкающих к узлу i и входящих в контур j, будем опускать.
», где p, q – соответственно множество ветвей, примыкающих к узлу i и входящих в контур j, будем опускать.
Электрическая подсистема
Уравнения равновесия определяют равенство нулю суммы токов в узлах сопряжения элементов; их находят по первому закону Кирхгофа:
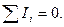 (9)
(9)
Уравнения неразрывности соответствуют второму закону Кирхгофа. Они выражают равенство нулю суммы падений напряжений на элементах схемы, образующих контур:
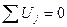 . (10)
. (10)
Механическая подсистема
Уравнения равновесия отражают принцип Д' Аламбера: сумма сил, действующих на тело, включая инерционные, равна нулю:
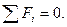 (9 а)
(9 а)
Для вращательных подсистем суммируются моменты сил, действующих относительно оси вращения.
Уравнения неразрывности определяются принципом сложения скоростей: абсолютная скорость является суммой относительной и переносных скоростей (которых может быть несколько: с первого тела на второе, со второго на третье и т. д.).
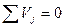 . (10 а)
. (10 а)
Для вращательных подсистем следует суммировать угловые скорости.
Гидравлическая (пневматическая) подсистема
Уравнения равновесия определяют равенство нулю потоков Q, подтекающих к узлу или оттекающих от него:
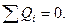 (9 б)
(9 б)
Уравнения неразрывности соответствуют сумме падений давлений при обходе по контуру:
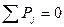 . (10 6)
. (10 6)
Тепловая подсистема
Уравнения равновесия определяют равенство нулю суммы тепловых потоков 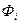 , подтекающих или оттекающих от узла, т. е.
, подтекающих или оттекающих от узла, т. е.
 (9 в)
(9 в)
Уравнения неразрывности соответствуют сумме разности температур Tj на участках, входящих в замкнутый контур:
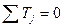 . (10 в)
. (10 в)
Источники энергии типа потока J и разности потенциалов Е делят на независимые и зависимые.
Независимые источники используют для моделирования постоянных воздействий на объект, например, сила тяжести может быть отражена постоянным источником силы F, напряжение питания электрической схемы – источником типа разности потенциалов.
Зависимые источники делят на две группы: источники, зависимые от времени, и источники, зависимые от фазовых переменных. Первые используют для моделирования внешних воздействий, вторые – для отражения нелинейных свойств объекта, а также для отражения взаимосвязей между подсистемами различной физической природы.
Примером взаимной зависимости двух подсистем p и q различной физической природы может служить трансформаторная связь этих подсистем (см. рис. 6). Зависимый источник разности потенциалов в одной подсистеме зависит от разности потенциалов на зависимом источнике потока другой подсистемы, который, в свою очередь, зависит от потока через первый источник.
Эквивалентные схемы технических объектов строят путем объединения в ансамбль всех элементов подсистем (в том числе различной физической природы), образующих данный технический объект. В эквивалентной схеме отражаются элементы и свойства реального объекта, оказывающие существенное влияние на его функционирование.
Двухполюсники (см. рис. 2...6), моделирующие элементы и (или) компоненты подсистем, соединяют между собой в соответствии со структурой подсистемы и с учетом функциональных связей между компонентами. В первую очередь рекомендуется объединять наиболее существенные элементы. Так, при моделировании механических подсистем вначале выделяют компоненты типа массы. Один из полюсов двухполюсника (рис. 2, б) соединяют с базовым узлом, отражающим инерциальную систему отсчета, второй полюс характеризует воздействие этой массы на некоторые элементы объекта, поэтому его следует соединить с полюсами этих элементов. Далее в механической подсистеме выделяют элементы трения и упругости. Элементы трения (рис. 4) включают между контактирующими телами, элементы упругости (рис. 3) – между телами, соединенными упругой связью. Внешние силы отображают включением источника силы между базисным и тем узлом, к которому подключен элемент массы, подверженной действию этой силы.
Построение эквивалентных схем рассмотрим на конкретных примерах.
Муфта сцепления автомобиля (рис. 7) служит для регулирования плавного соединения коленчатого вала 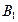 двигателя с первичным валом
двигателя с первичным валом 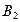 коробки передач.
коробки передач.
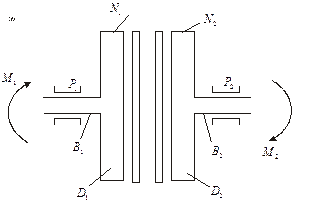
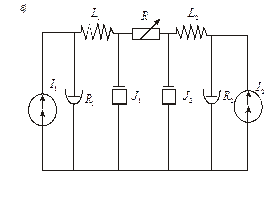
Рис. 7.Муфта сцепления (а) и её эквивалентная схема (б)
Крутящий момент 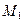 через вал
через вал 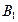 имеющий крутильную жесткость
имеющий крутильную жесткость  передается на маховик и диск
передается на маховик и диск 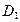 с фрикционной накладкой
с фрикционной накладкой 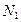 . Суммарный момент инерции ведущего диска равен
. Суммарный момент инерции ведущего диска равен 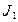 . Небольшая часть крутящего момента теряется в подшипнике
. Небольшая часть крутящего момента теряется в подшипнике 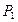 с коэффициентом трения
с коэффициентом трения 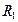 . Когда диски прижаты друг к другу, крутящий момент через фрикционные накладки
. Когда диски прижаты друг к другу, крутящий момент через фрикционные накладки  передается на ведомый диск
передается на ведомый диск  и далее через вал
и далее через вал 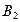 , на коробку передач.
, на коробку передач.
Эквивалентная схема полностью отражает механизм передачи крутящего момента 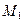 от двигателя до коробки передач. Момент
от двигателя до коробки передач. Момент 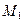 моделируется током
моделируется током 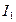 трение в подшипнике
трение в подшипнике 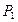 – резистором
– резистором 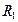 , гибкость вала
, гибкость вала 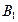 – индуктивностью
– индуктивностью  , масса ведущего диска – моментом инерции
, масса ведущего диска – моментом инерции 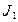 . Работу фрикционных накладок отражает резистор R. Дальнейшая передача момента от диска
. Работу фрикционных накладок отражает резистор R. Дальнейшая передача момента от диска  до коробки передач аналогична рассмотренной.
до коробки передач аналогична рассмотренной.
Примером механической поступательной системы (рис. 8) служит автомобиль массой 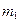 , который перевозит груз массой
, который перевозит груз массой 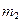 и прицеп массой
и прицеп массой 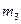 . В прицепе находится подпружиненный груз массой
. В прицепе находится подпружиненный груз массой  .
.
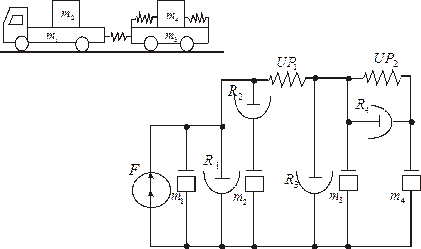
Рис. 8.Поступательная механическая система и её эквивалентная схема:
На рисунке F – тяга автомобиля; 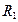 и
и 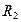 – приведенные коэффициенты трения между грузами и кузовами автомобиля и прицепа;
– приведенные коэффициенты трения между грузами и кузовами автомобиля и прицепа; 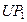 и
и 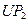 – упругости сцепления и пружины крепления груза к прицепу
– упругости сцепления и пружины крепления груза к прицепу
В качестве примера системы, состоящей из электрической, механической и пневматической подсистем, рассмотрим вибронасос (рис. 9). Под воздействием переменного магнитного поля, возникающего в зазоре электромагнита, приходит в движение груз массой т. Этот груз, шарнирно связанный через рычаг с насосом, действует на сильфон S, который, пульсируя, прокачивает воздух через клапаны k.

Рис. 9.Схема вибронасоса
В устройстве можно выделить конструктивно самостоятельные простые подсистемы, доказанные на эквивалентной схеме замещения (рис. 10): обмотку электромагнита 1, электромагнит 2, рычажный механизм 3, сильфон и воздушную магистраль с клапаном Связи этих подсистем осуществляются гираторами для пар 1-2 и 3-4 и трансформатором – для пары 2-3.
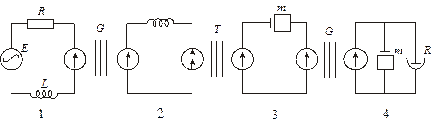
Рис.10.Эквивалентная схема замещения вибронасоса
17.4 Метод получения топологических уравнений
Эквивалентная схема технической системы может быть представлена в виде графа, ребра которого изображают двухполюсники, замещающие элементы (компоненты) системы. Пусть задан граф (рис. 11) некоторой технической системы. Топологические уравнения равновесия (типа уравнений первого закона Кирхгофа) могут быть записаны для каждого сечения, которое может включать один или несколько узлов. Для узлов, отмеченных на рис. 11, можем записать (принимая знак минус при направлении ребер к рассматриваемому узлу) следующие уравнения:
сечение 1 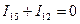 ;
;
сечение 1-5 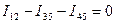 ;
;
сечение 2 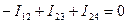 (11)
(11)
сечение 4 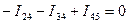 .
.
Топологические уравнения неразрывности (аналоги второго закона Кирхгофа) будут иметь вид:
 (12)
(12)
Процедура получения уравнений (11), (12) может быть формализована. Для этой цели вводят матрицу контуров и сечений – М-матрицу. Такую матрицу строят с помощью ориентированного графа эквивалентной схемы и выбранного для этого графа дерева. Количество столбцов матрицы соответствует числу ветвей дерева, а количество строк – числу хорд.
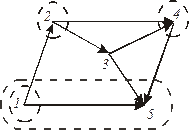
Рис.11.Граф эквивалентной схемы
При формировании М-матрицы хорды поочередно включают в дерево с образованием замкнутого контура. При обходе этого контура в направлении включенной хорды формируют строку матрицы. В столбцах матрицы, соответствующих ветвям дерева, ставят +1 при совпадении направления ветви с направлением обхода и -1, если направления противоположны.
Рассмотрим построение М-матрицы (табл. 1) для графа, показанного на рис. 11. Принимая пятый узел за базовый, построим дерево графа (рис. 12). При подключении хорды 1-2 образуется контур 1-2, 2-3, 3-5, 1-5, поэтому в первой строке матрицы будем иметь ‒ 1 (для ветви 1-5), + 1 (для ветвей 2-3, 3-5) и 0 (для ветви 3-4). Аналогично заполняют остальные строки.
Таблица 10.2
| Хорды | Ветви дерева | |||
| 1 – 5 | 3 – 5 | 2 – 3 | 3 – 4 | |
| 1 – 2 2 – 4 4 – 5 | -1 | -1 | -1 | -1 |
Топологические уравнения с использованием М-матрицы имеют вид:
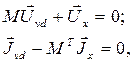 (13)
(13)
где 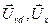 – векторы переменных типа разности потенциалов на ветвях дерева и хордах;
– векторы переменных типа разности потенциалов на ветвях дерева и хордах;
 – векторы переменных типа потока для ветвей дерева и хорд.
– векторы переменных типа потока для ветвей дерева и хорд.
Записывая первое уравнение (13) в развернутом виде

вы можете убедиться, что оно совпадает с системой уравнений (12). Аналогично, второе уравнение (13) совпадает с (11). Таким образом, использование М-матрицы позволяет формализовать процедуру получения математической модели. При этом сечения дерева специально выбирать не надо. Выше такие сечения приведены для наглядности.
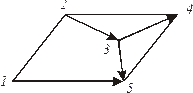
Рис.12. К построению М-матрицы
Возможна иная формализация процедуры построения математической модели с использованием матрицы инциденций. Будем рассматривать исходный граф (см. рис, 11) как хорды некоторого фиктивного дерева (рис. 13), ветви которого на рисунке изображены пунктирными линиями.
Составим М-матрицу, поочередно включая в фиктивное дерево хорды исходного графа. Так, контур 1-5 состоит из хорды 1-5 и ветви 1-5, направление которой противоположно хорде, поэтому в М-матрице этой ветви будет отвечать значение – 1. В контуре 2-3-5 направление ветви 3-5 совпадает с направлением хорды, а для ветви 2-5 – не совпадает, поэтому будем соответственно иметь +1 и -1. Включая последовательно все хорды, получим М-матрицу (рис. 13), приведенную в табл. 2, или, выделяя содержательную часть М-матрицы.
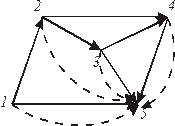
Рис.13.Граф с фиктивным деревом
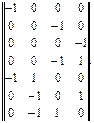 (14)
(14)
Таблица 10.3
| Хорды | Ветви дерева | |||
| 1 – 5 | 2 – 5 | 3 – 5 | 4 – 5 | |
| 1 – 5 3 – 5 4 – 5 3 – 4 1 – 2 2 – 4 2 – 3 | -1 -1 | -1 -1 | -1 -1 | -1 |
Рассмотрим второе уравнение  системы (13), которое будет справедливо для М-матрицы (14), но с некоторым отличием. Это отличие связано с тем, что было построено фиктивное дерево, поэтому в ветвях его не будет токов
системы (13), которое будет справедливо для М-матрицы (14), но с некоторым отличием. Это отличие связано с тем, что было построено фиктивное дерево, поэтому в ветвях его не будет токов  и, следовательно, исходное уравнение примет вид
и, следовательно, исходное уравнение примет вид  . Индекс «х» у вектора J мы опустили, поскольку хордами являются все ребра исходного графа. Обратите внимание, что транспонированная М-матрица представляет собой не что иное, как матрицу
. Индекс «х» у вектора J мы опустили, поскольку хордами являются все ребра исходного графа. Обратите внимание, что транспонированная М-матрица представляет собой не что иное, как матрицу  инциденций исходного графа (см. рис.), записанную с обратными знаками:
инциденций исходного графа (см. рис.), записанную с обратными знаками:
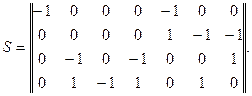 (15)
(15)
Все это позволяет записать второе уравнение системы (13) в ином виде: 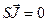 .
.
Первое уравнение системы (13) изменится следующим образом. Разность потенциалов ветвей дерева Uvd есть разность потенциалов i- й и базовой точек, т. е. потенциал i- й точки 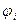 . М-матрица будет равна
. М-матрица будет равна  , поэтому первое уравнение системы (13) примет вид
, поэтому первое уравнение системы (13) примет вид 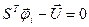 .
.
Все сказанное дает возможность записать систему уравнений (13) в следующей форме:
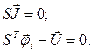 (16)
(16)
Таким образом, возможны два способа формализации процедур построения математической модели для описания эквивалентной схемы технического объекта, в одном из которых используют систему уравнений (13) и М-матрицу, в другом – систему уравнений (16) и матрицу инциденций ориентированного графа.
В качестве примера рассмотрим механическую систему (рис. 14, а), эквивалентная схема (б) и граф (в) которой изображены на рисунке. Матрица инциденций приведена в табл. 3.
Таблица 3
| Узлы графа | Дуги графа | ||||||||
| F | R1 | L1 | L2 | R2 | R3 | m1 | m2 | m3 | |
| -1 | -1 | -1 |

Рис. 14.К примеру механической системы
Первое уравнение (16) в развернутой форме имеет вид:

где потоковые переменные JR, JL, Jm=Jc типов R, L, С можно записать в форме приведенных выше зависимостей между фазовыми переменными. В результате будет получена система дифференциальных уравнений. Транспонируя матрицу инциденций и используя второе уравнение системы (16), аналогично можно получить систему дифференциальных уравнений для переменных типа потенциала.
Литература:
1. Ильина Н.В. Системный анализ и моделирование процессов в техносфере: Учеб. пособие / Н.В. Ильина, Д.Д. Лапшин, В.И. Федянин. – Ч. 1. Воронеж: ГОУВПО «Воронежский государственный технический университет, 2008. – 206 с.
Лекция 18. Многокритериальная оптимизация
18.1 Свойства задач принятия решения со многими критериями
В технической практике задачи ПР с учетом нескольких критериев возникают достаточно часто. Сложность подобных задач существенно выше, чем при наличии одного критерия. Если при этом еще учитывать и неоднозначность внешних воздействий, то для получения корректного результата кроме математических знаний необходим также и опыт в соответствующей предметной области.
Теоретически можно представить случай, когда во множестве 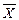 окажется одна альтернатива, для которой все r критериев (целевых функций) принимают наибольшие значения (в предположении, что все критерии максимизируются). Естественно, что данная альтернатива и будет наилучшей. К сожалению, на практике такие ситуации практически не встречаются, а типичным является случай, представленный на рис. 1, для двух целевых функций.
окажется одна альтернатива, для которой все r критериев (целевых функций) принимают наибольшие значения (в предположении, что все критерии максимизируются). Естественно, что данная альтернатива и будет наилучшей. К сожалению, на практике такие ситуации практически не встречаются, а типичным является случай, представленный на рис. 1, для двух целевых функций.
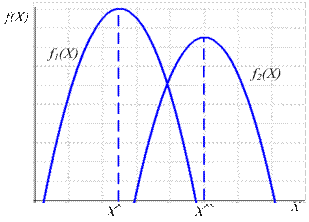
Рис. 1. Ситуация ПР для двух критериев
При Х* максимума достигает одна целевая функция, а при Х** – другая; нам же предстоит сделать только один выбор. Очевидно, что ППР здесь становится менее прозрачным.
Сформулируем некоторые очевидные положения для подобных ситуаций:
1. Не существует результата наилучшего в абсолютном смысле.
2. Решение может считаться лучшим лишь для конкретного ЛПР, с учетом его предпочтений.
3. Для нахождения приемлемого результата должна строиться многокритериальная модель, которая создается для уточнения предпочтений ЛПР. Она должна быть логически непротиворечивой и должна включать в себя основные свойства решаемой задачи.
Прежде чем переходить к рассмотрению многокритериальных задач, остановимся на предпосылкахих постановки, т.е. укажем причины, порождающие проблему многокритериальности. Для этого обратимся к блок-схеме, приведенной на рис. 2 в лекции 2 (рис. 2). Данная схема отражает рациональную логическую последовательность этапов при подготовке и принятии решений.
С проблемой многокритериальности лицо, принимающее решение, сталкивается на этапе 7 (Выбор наиболее предпочтительного вариата решения). Вместе с тем, ЛПР на более ранних этапах (2 и 3 при формулировании цели и критериев оценки) сам предопределяет постановку многокритериальной задачи. Следовательно, предпосылкой постановки многокритериальной задачи является необходимость проведения этапа 3 (формирования системы критериев). Этот этап может и отсутствовать, если цель принятия решения четко определяется одним критерием.
В практических задачах цель – весьма сложное понятие, которое даже содержательно не всегда удастся четко определить, тем более, количественно измерить степень ее достижения. Поэтому осуществляется декомпозиция сложного понятия " цель принятия решения" на более простые единичные критерии, каждый из которых может быть количественно измерен. В большинстве случаев в качестве единичных критериев используются общепринятые характеристики исследуемого объекта, измеряемые по шкалам интервалов или отношений.
Полное и четкое описание цели множеством критериев является основой успешного решения поставленной задачи принятия решений.
Таким образом, причинами проведения этапа 3 и, соответственно, предпосылками постановки многокритериальных задач являются сложность цели принятия решений и трудность измерения степени достижения цели различными вариантами решения задачи.

Рис. 2. Этапы подготовки и принятия решений
Следовательно, постановку многокритериальной задачи предопределяет сам исследователь (ЛПР) из-за того, что не смог сформировать в математическом виде целевую функцию, а на этапе 7 он сталкивается с необходимостью решения многокритериальной задачи.
Следует отметить, что поскольку описание цели системой критериев является неформальной процедурой, то и последующее агрегирование критериев на этапе 7 также не является формальной процедурой. Поэтому решение многокритериальной задачи не является строгой математической задачей, а представляет собой набор процедур, помогающих ЛПР разобраться и уточнить цель принятия решений, устранить ошибки в своих оценках, сделать свое поведение в процессе выбора рациональным.
Примеры постановок многокритериальных задач из разных областей деятельности:
Выбор площадок для строительства промышленных объектов. В данной задаче необходимо учитывать группы критериев: экономические, экологические, социальные, критерии безопасности и т.д.
Оценка качества продукции (технического уровня разработок) по множеству потребительских свойств. Следствием данной задачи является определение цены на продукцию на основе потребительских свойств.
Проектирование на основе принципа многовариантности. Каждый из вариантов в абсолютном большинстве оценивается множеством критериев. В этой связи следует подчеркнуть, чтосистемы автоматизированного проектирования должны включать подсистему выбора и оценки решений по многим критериям.
Проведем классификацию многокритериальных задач (рис. 3).
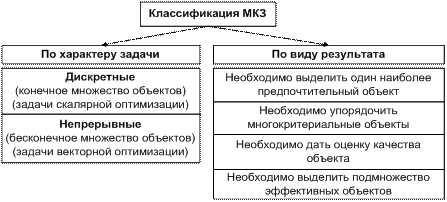
Рис. 3. Классификация МКЗ
По характеру решаемой многокритериальной задачи (МКЗ) можно выделить два класса задач.
Задачи, в которых множество объектов конечно, будем называть дискретными многокритериальными задачами (ДМКЗ). В задачах этого класса множество многокритериальных объектов в пространстве критериев f 1´ f 2´ ... ´ fm представляет собой множество дискретных точек. Дискретные МКЗ чаще всего ставятся в экономике и квалиметрии.
Второй класс образует непрерывные многокритериальные задачи (НМКЗ), которые формулируются следующим образом:
Имеется объект исследования, характеризующийся параметрами x 1,..., xn. Требуется определить оптимальные в некотором смысле значения этих параметров с учетом нескольких критериев (целевых функций) k 1,..., km. При этом задана область определения параметров x 1,..., xn и целевые функции k 1 =f 1 (x 1,..., xn);...; km=fm(x 1,..., xn).
Область определения параметров (переменных) задается обычно в виде системы ограничений, например, в многокритериальных задачах линейного программирования – система линейных неравенств. Поэтому непрерывную многокритериальную задачу можно рассматривать как задачу, в которой бесконечное множество объектов.
Так как непрерывные МКЗ, как правило, возникают при оптимизации параметров сложных объектов, то в литературе их еще называют задачами векторной оптимизации. Одной из задач векторной оптимизации является многокритериальная задача линейного программирования.
Будем называть каждый из скалярных критериев оптимальности  частным критерием оптимальности. Совокупность частных критериев оптимальности
частным критерием оптимальности. Совокупность частных критериев оптимальности  будем называть векторным критерием оптимальности. Предполагаем, что ставится задача оптимизации каждого из частных критериев оптимальности
будем называть векторным критерием оптимальности. Предполагаем, что ставится задача оптимизации каждого из частных критериев оптимальности 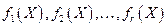 в одной и той же области допустимых значений D.
в одной и той же области допустимых значений D.
Вторым признаком классификации многокритериальных задач является вид требуемого результата решения задачи. По этому признаку выделим следующие классы многокритериальных задач:
задачи, в которых необходимо выделить из множества объектов один наиболее предпочтительный объект (получить одно наиболее предпочтительное решение). В некоторых случаях может быть выделено не одно, а подмножество эквивалентных и наиболее предпочтительных объектов. Постановка задачи выделения наиболее предпочтительного объекта может быть как для дискретных, так и для непрерывных многокритериальных задач;
задачи, в которых необходимо упорядочить многокритериальные объекты. Постановка многокритериальной задачи в таком виде чаще всего имеет место для дискретных МКЗ, например, упорядочить по предпочтению варианты технических систем, по качеству – образцы продукции;
задачи, в которых требуется дать оценку полезности (качества) объектов по шкале интервалов. Другими словами, необходимо построить функцию полезности. Очевидно, что такая постановка задачи может быть как для дискретных, так и для непрерывных МКЗ;
задачи, в которых требуется выделить подмножество эффективных (конкурирующих) объектов. Такие подмножества называют оптимальными по Парето, но об этом более подробно поговорим чуть позже.
18.2. Формирование множества критериев
Количество критериев должно охватывать все особенности задачи. Число критериев считается полным и достаточным, если прибавление нового критерия не изменит результата решения, а отбрасывание критерия этот результат меняет. Все критерии не должны сильно коррелировать друг с другом. Степень корреляции между μ и ν критериями можно определить по следующей формуле:
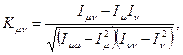
где 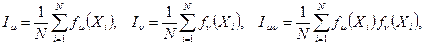
где Хi – случайная альтернатива из множества 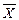 , i=1, …, N; fμ (Хi), fν (Хi) – критерии; N – число случайных испытаний.
, i=1, …, N; fμ (Хi), fν (Хi) – критерии; N – число случайных испытаний.
Если K mn приближается к 1, то это свидетельствует о сильной корреляции критериев. Тогда необходимо рассмотреть вопрос об исключении одного из критериев.
Каждому критерию может быть поставлена в соответствие своя координатная ось и шкала. Последняя может быть непрерывной или дискретной, количественной или качественной (рис. 4).

Рис. 4. Выбор альтернативы с учетом двух критериев: а — в случае непрерывной области альтернатив; б — в случае дискретных альтернатив
Каждую ось будем обозначать буквой fk, k = 1, 2, …, r. f 1 × f 2 ×... × fr – декартово произведение, которое формирует пространство критериев, где имеет место множество векторных оценок. Между пространством параметров и пространством критериев существует соответствие (рис. 5).
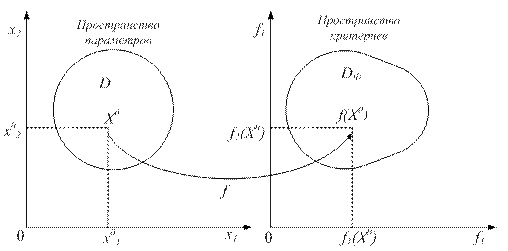
Рис. 5. Пространства параметров и критериев:
D – допустимая область, DФ – аналог допустимой области в пространстве критериев
18.3 Методология решения многокритериальных задач
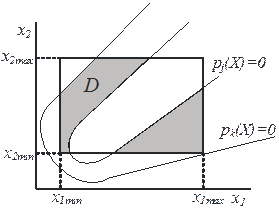
При решении многокритериальных задач обычно задаются параметрические ограничения вида xi min ≤ xi ≤ xi mах, при i=1, 2, …, n, которые формируют в пространстве параметров n-мерный параллелепипед (рис. 4, а). Далее предполагается, что заданы функциональные ограничения вида pj (x) ≤ 0, при j=1, 2, …, m, которые вырезают в параллелепипеде некоторую часть D, состоящую из точек Х, удовлетворяющих одновременно параметрическим и функциональным ограничениям. В лекции 5 эту часть пространства мы называли допустимой областью (ДО). Множество D может оказаться весьма сложным, например, состоящим из нескольких отдельных частей (рис. 6, б, закрашенные участки).
Наконец, предполагается, что заданы соответствующие критерии fk (Х i), k =1, 2, …, r. Для определенности здесь будем считать, что критерии f 1, …, fr желательно уменьшить.
Предположим, что ЛПР сумел указать разумные критериальные ограничения вида 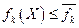 , при k =1, 2, …, r. При этом
, при k =1, 2, …, r. При этом 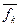 – значение для одной из линий равного уровня n -го критерия.
– значение для одной из линий равного уровня n -го критерия.
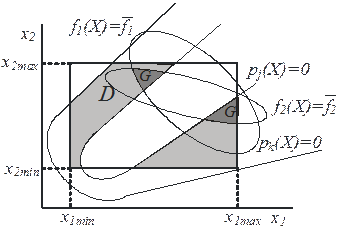
Очевидно, 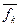 – это наихудшее значение критерия, на которое ЛПР может согласиться. Обозначим через G множество точек Х, которые удовлетворяют параметрическим, функциональным и критериальным ограничениям. Понятно, что
– это наихудшее значение критерия, на которое ЛПР может согласиться. Обозначим через G множество точек Х, которые удовлетворяют параметрическим, функциональным и критериальным ограничениям. Понятно, что 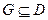 (рис. 6, в, закрашенные области).
(рис. 6, в, закрашенные области).

а)
б)
в)
Рис. 6. Формирование параметрическими (а), функциональными (б) и критериальными (в) ограничениями области поиска экстремума
Наилучшее решение целесообразнее искать среди точек множества G, а не среди точек множества D, поскольку, если точка 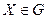 , то значения всех критериев в этой точке приемлемы. Понятно, что завышенные требования ЛПР могут привести к G=0, т.е. область поиска решений окажется пустой.
, то значения всех критериев в этой точке приемлемы. Понятно, что завышенные требования ЛПР могут привести к G=0, т.е. область поиска решений окажется пустой.
При решении многокритериальных задач выбора основная трудность состоит в неоднозначности выбора наилучшего решения. Для ее преодоления используют две группы методов.
В методах первой группы стремятся сократить число критериев, для чего вводят дополнительные предположения, относящиеся к процедуре сопоставления критериев и построению моделей оптимизации. В методах первой группы стремятся сократить число альтернатив в исходном множестве, исключив заведомо плохие альтернативы.
К методам первой группы относятся метод свертки, метод главного критерия, метод пороговых критериев и метод расстояния.
Методы второй группы основаны на свертке в множестве альтернатив. С их помощью пытаются уменьшить число возможных вариантов решений, исключив заведомо плохие. Один из подходов, обладающий большой общностью, называется методом, основанным на принципе Парето. Для уменьшение числа альтернатив исходного множества выделяют множество Парето, являющееся подмножеством исходного.
После того, как построено множество Парето, для определения наилучшего решения (из оставшихся) применяются методы первой группы либо графические методы, например, метод диаграмм. Схема поиска наилучшего решения представлена на рис. 7.
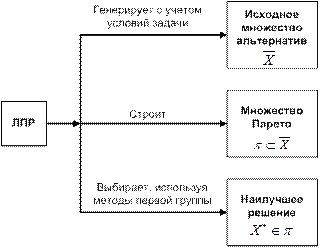
Рис. 7. Схема поиска наилучшего решения
Подчас необходимые для определения предпочтений знания в области ТПР, умения и навыки у ЛПР отсутствуют, а требуемые для совершения этой работы активные ресурсы – время, деньги, специальное математическое обеспечение и т. п. – отсутствуют в нужных количествах. Да ведь и не все проблемы, возникающие перед ЛПР, на практике оказываются столь важными, чтобы обязательно и как можно более точно моделировать его предпочтения. Как тут быть? Во всех перечисленных случаях для отыскания, наилучшей альтернативы ТПР рекомендует ЛПР следовать принципу Родена. Когда у этого великого скульптора спросили, как ему удается создавать столь великие шедевры, Роден ответил: «Я просто беру глыбу мрамора и отсекаю от нее все лишнее!».
Прекрасная идея: последовательно отсекайте от множества альтернатив все элементы, которые «не нужны», которые являются «лишними», а то, что останется (не лишнее) – это и есть то, что вам нужно – наилучшая альтернатива (или несколько эквивалентных по предпочтительности наилучших альтернатив). Концептуальную идею, изложенную в вербальной форме Роденом, реализовал в формальном виде и превратил в одну из наиболее эффективных функций выбора видный социолог и итальянский экономист Вильфредо Парето в 1897 году.
Он рассматривал распределение богатства и доходов в Англии XIX века. Он выяснил, что большая часть доходов и материальных ценностей принадлежит меньшинству людей в исследованных группах. Возможно, что для Парето не было в этом ничего удивительного. Однако он также установил два очень примечательных, по его мнению, факта. Первым был тот, что существует неизменное математическое соотношение между численностью группы людей (в процентах от общей численности рассматриваемого населения) и долей богатства или дохода, контролируемой этой группой. Другими словами, если известно, что 20% населения владеют 80% материальных ценностей, то можно с уверенностью сказать, что 10% населения имеют приблизительно 65% материальных ценностей, а 5% населения — 50%. Для Парето главным здесь были не цифры процентного соотношения, а тот факт, что распределение богатства среди населения предсказуемо несбалансированно.
Другой находкой Парето, восхитившей его, было то, что данная схема дисбаланса оставалась неизменной для статистических данных, относящихся к различным периодам времени и различным странам. Будь то данные по Англии за любой период ее истории или доступные Парето данные по другим странам за разные периоды времени, выяснялось, что схема снова и снова повторяется, причем с математической точностью.
Его открытие называли по-разному, в том числе принципом Парето, законом Парето, правилом 80/20, принципом наименьшего усилия, принципом Дисбаланса.
Принцип 80/20 гласит, что небольшая доля причин, вкладываемых средств или прилагаемых усилий, отвечает за большую долю результатов, получаемой продукции или заработанного вознаграждения. Например, на получение 80% результатов, достигаемых в работе, у вас уходит 20% всего затраченного времени. Выходит, что на практике 4/5 приложенных вами усилий (немалая доля) не имеют к получаемому результату почти никакого отношения. Это, кстати, расходится с тем, чего люди обычно ожидают.
Введем на множестве D отношение предпочтения (обозначим его символом 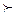 ). Будем говорить, что вектор
). Будем говорить, что вектор  предпочтительнее вектора
предпочтительнее вектора 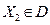 , и писать
, и писать  , если среди равенств и неравенств
, если среди равенств и неравенств  имеется хотя бы одно строгое неравенство (рис. 6).
имеется хотя бы одно строгое неравенство (рис. 6).
Аналогично на множестве DФ введем отношение доминирования: будем говорить, что векторный критерий оптимальности 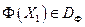 доминирует векторный критерий оптимальности
доминирует векторный критерий оптимальности 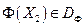 , и писать
, и писать 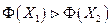 , если
, если  .
.
Другими словами, объект 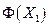 доминирует объект
доминирует объект 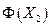 , если по всем критериям
, если по всем критериям 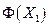 предпочтительнее или эквивалентен
предпочтительнее или эквивалентен 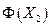 , и хотя бы по одному критерию строго предпочтительнее. Объект
, и хотя бы по одному критерию строго предпочтительнее. Объект 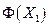 называют доминирующим, а
называют доминирующим, а 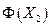 – доминируемым.
– доминируемым.
Если исключить из исходного множества доминируемые объекты, то останутся конкурирующие (эффективные).
Введенные отношение предпочтения и отношение доминирования являются транзитивными, т.е.
если  и
и  , то
, то 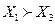 ;
;
если 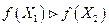 и
и 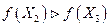 , то
, то 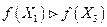
Выделим из множества DФ подмножество  точек, для которых нет точек, их доминирующих. Множество
точек, для которых нет точек, их доминирующих. Множество 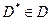 , соответствующее
, соответствующее 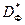 , называется множеством Парето (переговорным множеством, областью компромисса) — рис. 7. Поскольку множество DФ на рисунке 7 является выпуклым, то множество
, называется множеством Парето (переговорным множеством, областью компромисса) — рис. 7. Поскольку множество DФ на рисунке 7 является выпуклым, то множество 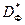 - есть часть границы множества DФ — дуга AB, в которой точка A соответствует f1min, а точка B - f2min. Среди точек
- есть часть границы множества DФ — дуга AB, в которой точка A соответствует f1min, а точка B - f2min. Среди точек
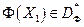 ,
, 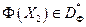
нет более предпочтительных, поскольку
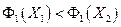 , но
, но 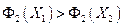 .
.
Таким образом, если 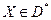 , то
, то 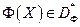 .
.
Другими словами множество Парето можно определить как множество, в котором значение любого из скалярных (частных) критериев оптимальности можно улучшить только за счет ухудшения других частных критериев – любое из решений, принадлежащее множеству Парето, не может быть улучшено одновременно по всем частным критериям.
Альтернатива принадлежит множеству Парето, если она не хуже других по всем критериям и хотя бы по одному критерию лучше.

Рис. 8. Множество Парето
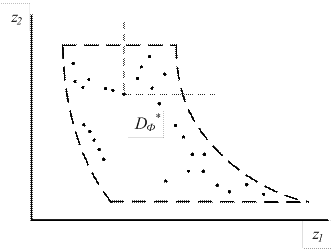
Для пояснения изложенного рассмотрим простейший метод, позволяющий приближенно находить множество Парето для случая двух критериев. На рис. 8, а построена область возможных значений 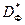 в плоскости двух критериев. Исключение неэффективных точек в этом случае очень наглядно. Исключению подлежат все точки, образы которых в плоскости (f1, f2) расположены одновременно правее и выше образа исходной точки. В случае многих критериев геометрическая интерпретация аналогична.
в плоскости двух критериев. Исключение неэффективных точек в этом случае очень наглядно. Исключению подлежат все точки, образы которых в плоскости (f1, f2) расположены одновременно правее и выше образа исходной точки. В случае многих критериев геометрическая интерпретация аналогична.
После исключения неэффективных точек осталось всего 9 приближенно эффективных точек. Соединив их, получим приближенную компромиссную кривую E, которая вместе с точной компромиссной кривой D* построена на рис. 9, б. В качестве наилучшей среди исходной совокупности точек следует выбрать одну из этих 9 точек.
 а)
а)
 б)
б)
Рис. 9. Построение области Парето
Например, Андрей лучше всех решает задачи, а по остальным критериям не выделяется. Зато Вера, Галя, Ира, Катя, Лариса имеют высокие значения остальных критериев, так что они в среднем превосходят Андрея, причем Вера лучше всех по успеваемости, а по остальным критериям не хуже других студенток. Тогда Андрей обзятельно попадает в множество Парето, т.к. он уникальный (единственный) по первому критерию, а от группы студенток в множество Парето попадает один представитель – Вера, хотя остальные студентки превосходят Андрея по нескольким критериям (число критериев здесь не имеет значения).
Таким образом, поиск оптимального решения (точки) может осуществляться в соответствии с рисунком 10.
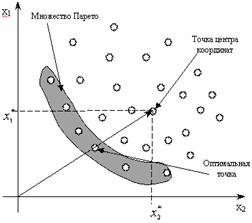
Рис. 10. Выбор оптимальной точки
18.4 Технологии отыскания эффективных решений
Суждения об относительной важности частных критериев ЛПР может выразить как в качественной, так и в количественной шкале. Если частные критерии измеряются в различных, а тем более разных по классам шкалах (количественных и качественных), их оценки не могут быть пересчитаны в некоторую объективную шкалу оценивания (например, в универсальный денежный эквивалент), то трудно представить, как соизмерить их относительную важность. А сделать это иногда требуется как можно быстрее и как можно адекватнее, чтобы можно было сразу представить себе ценность какой-то конкретной альтернативы. В подобных ситуациях, когда информацию об относительной важности требуется получить и использовать как можно быстрее и при этом обеспечить высокую адекватность и надежность суждений, более предпочтительным представляется учет относительной важности частных критериев в качественной шкале (так называемая «качественная информация об относительной важности»). К качественной информации об относительной важности частных критериев будем относить следующие вербальные суждения:
«критерий с номером i важнее критерия с номером j»;
«критерии с номерами s и t равноценны по важности».
Напрямую использовать информацию о превосходствеили равноценности для дальнейшего сокращения размера множества эффективных альтернатив и поиска наилучшего решения среди них можно только для некоторых частных случаев. Во-первых, это случай, когда шкалы всех частных критериев, относительно которых получена информация.
Второй частной ситуацией, когда возможно прямое использование качественной информации о равноценности или превосходстве в важности одних частных критериев над другими, является такая, в рамках которой фигурируют сообщения о равноценности всех критериев между собой, об абсолютно строгом (лексикографическом) упорядочении критериев по важности, а также о симметрически-лексикографическом упорядочении частных критериев по важности.
Самая сложная в получении, но и самая действенная – это информация об относительной важности критериев в количественной форме. Это информация о величинах замещений значений критериев между собой, о значениях коэффициентов важности частных критериев, количественная информация о допустимой степени взаимной компенсации значений тех или иных критериев, а также о виде функции агрегирования частных критериев в обобщенные критерии. В некоторых случаях такая информация поступает от ЛПР сразу. Но это – скорее исключение из правил. Значительно чаще количественную информацию приходится получать по частям.
18.5 Методы принятия решения при нескольких критериях
При необходимости ПР при многих критериях на практике обычно используют следующие подходы.
1. Свертка векторного критерия
Этот метод также называют скаляризацией векторного критерия или введением суперкритерия. Суть его заключается в следующем.
Выбираются коэффициенты β k ≥ 0 так, что функция
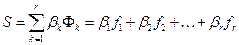
обобщила в себе" все требования частных критериев. При этом обычно
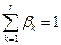
и каждый β k характеризует степень важности критерия fk(X).
На практике обычно ЛПР выбирает какие-то β 1, …, β r, затем отыскивает наилучшую точку Х' – например, минимум S(X') при 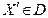 . Если при этом оказывается, что некоторые из значений ЛПР не удовлетворяют, тогда он корректирует значения β 1, …, β r и решает задачу заново и т.д.
. Если при этом оказывается, что некоторые из значений ЛПР не удовлетворяют, тогда он корректирует значения β 1, …, β r и решает задачу заново и т.д.
Рассмотренный подход также называют аддитивной сверткой. Он имеет существенный недостаток – трудно находить коэффициенты β k из-за разных размерностей критериев.
Этого недостатка лишена свертка вида:
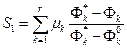 или
или 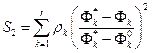 ,
,
где  – идеальное (реально недостижимое) значение k -го критерия, которое указывается ЛПР;
– идеальное (реально недостижимое) значение k -го критерия, которое указывается ЛПР;  – наименее предпочтительное для ЛПР значение k -го критерия; μ k, ρ k – весовые коэффициенты с тем же смыслом, что и β k. В двух последних свертках каждый k -й критерий выступает своим нормализованным значением
– наименее предпочтительное для ЛПР значение k -го критерия; μ k, ρ k – весовые коэффициенты с тем же смыслом, что и β k. В двух последних свертках каждый k -й критерий выступает своим нормализованным значением  , которое изменяется в пределах от 0 до 1. Данный подход снимает проблемы, обусловленные неодинаковыми размерностями входящих в свертку критериев.
, которое изменяется в пределах от 0 до 1. Данный подход снимает проблемы, обусловленные неодинаковыми размерностями входящих в свертку критериев.
Однако существуют и другие вопросы. В частности, можно показать, что выбор вида свертки влияет на конечный результат.
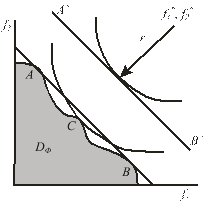
Для иллюстрации данного утверждения рассмотрим случай двух критериев Ф1 и Ф2 и предположим, что они оба получили одинаковые " веса": μ 1 = μ 2 =0, 5 и ρ 1 = ρ 2 =0, 5. Пусть допустимая область в пространстве критериев имеет вид, представленный на рис. 11 а.

а) б)
Рис. 11. Иллюстрация влияния вида свертки на конечный результат: а – допустимая область; б – линии равного уровня для критерия S1 (прямые) и S2 (окружности)
Для интегрального критерия типа S 1 линии равного уровня представляют собой прямые, задаваемые уравнениями:
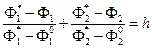
На рис. 11 б они показаны в виде линий АВ и A'B'. Для интегрального критерия типа S 2 линии равного уровня – окружности с центром в точке 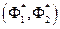 , которые описываются уравнением вида:
, которые описываются уравнением вида:
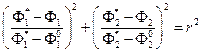
Из рис. 11 б видно, что первый тип рассматриваемой свертки предполагает выбор в качестве результата точки А или В; второй – точку С. Очевидно, что все три результата существенно отличаются друг от друга.
2. Оптимизация главного из нескольких критериев
При таком подходе один из критериев, наиболее важный с точки зрения ЛПР, оставляют в качестве единственного критерия, а все остальные заменяют ограничениями.
Пусть для определенности главным критерием считается f1(X). Тогда следует выбрать ограничения 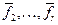 и рассмотреть задачу об отыскании минимума f1(X) при дополнительных ограничениях
и рассмотреть задачу об отыскании минимума f1(X) при дополнительных ограничениях 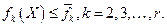
При таком подходе возникает проблема выбора критериальных ограничений  , что может потребовать выполнения специальных предварительных расчетов.
, что может потребовать выполнения специальных предварительных расчетов.
3. Последовательная оптимизация всех критериев
Сначала определяется минимальное значение f1(X) при 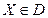 . Обозначим его через
. Обозначим его через 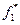 . Выбираем " уступку" по этому критерию h1 и назначаем критериальное ограничение
. Выбираем " уступку" по этому критерию h1 и назначаем критериальное ограничение 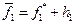 . Затем находится минимальное значение f2(Х) при
. Затем находится минимальное значение f2(Х) при 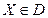 и дополнительном ограничении
и дополнительном ограничении 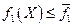 . Получив значение
. Получив значение  и выбрав " уступку" h2, назначаем второе кри
и выбрав " уступку" h2, назначаем второе кри