
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
По лабораторной работе №1
|
|
Отчёт
«Оптимизация температурного режима в реакторе идеального вытеснения»
Студент Широкова Анна
Преподаватель Егорова Е. В.
Вариант №23
Москва – 2012 г.
Постановка задачи.
В аппарате, который можно описать моделью идеального вытеснения происходит реакция превращения вещества А1 в вещество А2. Реакция обратимая экзотермическая, прямая реакция первого порядка по А1, обратная – по А2. Температура в зоне реакции регулируется теплообменом с поверхностью теплопередачи, температуру которой Тп можно считать постоянной по всей длине аппарата, а также температурой То жидкости, входящей в аппарат.
Цель работы.
Необходимо найти такое сочетание значений температуры на входе и температуры поверхности, при котором степень превращения реагента, (равная для этой реакции выходу продукта) окажется максимальной. При этом должно соблюдаться ограничение: ни в одной точке аппарата температура не должна превышать 110° С. (383 К) При этой температуре происходит вскипание растворителя, нарушающее нормальный ход процесса. Следует учесть, что в рассматриваемом процессе прирост выхода даже на 0, 1% даёт заметный эффект, и желательно, чтобы результат оказался как можно выше.
Ход работы.
Работа ведётся непосредственно с пульта ЭВМ, т.е. в диалоговом режиме. В ответ на вопрос машины задаются значения температуры на входе и температуры стенки. Обе управляющие температуры можно изменять в пределах от 20 до 110°С (293-383 К). После этого на экран выводится зависимость температуры внутри реактора от времени пребывания. Время отсчитывается от момента входа смеси в аппарат (10 точек, через каждую секунду). Зависимость выводится в виде таблицы и соответствующего ей графика.
Математическое описание (модель) процесса с учётом того, что реакция проводится в аппарате идеального вытеснения, состоит из уравнений описывающих изменение во времени концентраций реагентов и температуры:
dc1/dt = -k01*exp(-E1 /RT)*c1 – k02 *exp(-E2/RT)*c2
c2 = c01 – c1
dT/dt = ((E2 – E1)/(ρ *CT))*(- (dc1/dt)) – ((ά *fT)/(ρ *CT)*(T – Tп)
С начальными условиями при t = 0: c1 = c01, T = T0.
В процессе работы строится два графика. Один – ход температуры во времени. На этом графике -10 кривых, соответствующих моделируемым режимам. Второй график строится в координатах То – Тп. Каждая точка на этом графике соответствует одному из смоделированных режимов.
| Распределение температуры по времени | ||||||||||||||
| № опыта | То | Тп | выход | |||||||||||
| 60, 0 | 59, 6 | 59, 0 | 58, 2 | 57, 3 | 56, 3 | 55, 3 | 54, 2 | 53, 2 | 52, 2 | 51, 3 | 0, 436 | |||
| 95, 0 | 93, 1 | 89, 1 | 84, 3 | 79, 5 | 74, 9 | 70, 6 | 66, 7 | 63, 1 | 59, 9 | 57, 0 | 0, 532 | |||
| 100, 0 | 98, 2 | 93, 7 | 88, 3 | 83, 0 | 77, 9 | 73, 3 | 69, 1 | 65, 2 | 61, 8 | 58, 6 | 0, 537 | |||
| 105, 0 | 102, 9 | 97, 3 | 90, 9 | 84, 6 | 78, 8 | 73, 6 | 68, 8 | 64, 5 | 60, 6 | 57, 0 | 0, 539 | |||
| 105, 0 | 102, 4 | 96, 3 | 89, 5 | 82, 9 | 76, 8 | 71, 2 | 66, 2 | 61, 6 | 57, 5 | 53, 8 | 0, 539 | |||
| 105, 0 | 105, 4 | 102, 2 | 97, 8 | 93, 3 | 89, 1 | 85, 3 | 81, 8 | 78, 7 | 75, 9 | 73, 3 | 0, 541 | |||
| 108, 0 | 109, 0 | 105, 8 | 101, 4 | 97, 0 | 92, 9 | 89, 2 | 85, 8 | 82, 8 | 80, 0 | 77, 5 | 0, 541 | |||
| 109, 0 | 108, 6 | 103, 8 | 98, 1 | 92, 5 | 87, 4 | 82, 7 | 78, 5 | 74, 7 | 71, 2 | 68, 1 | 0, 542 | |||
| 109, 0 | 107, 6 | 101, 9 | 95, 3 | 89, 0 | 83, 3 | 78, 0 | 73, 3 | 69, 0 | 65, 1 | 61, 6 | 0, 542 | |||
| 80, 0 | 79, 1 | 77, 2 | 74, 8 | 72, 2 | 69, 6 | 67, 1 | 64, 7 | 62, 4 | 60, 4 | 58, 5 | 0, 512 |
Полученные результаты:
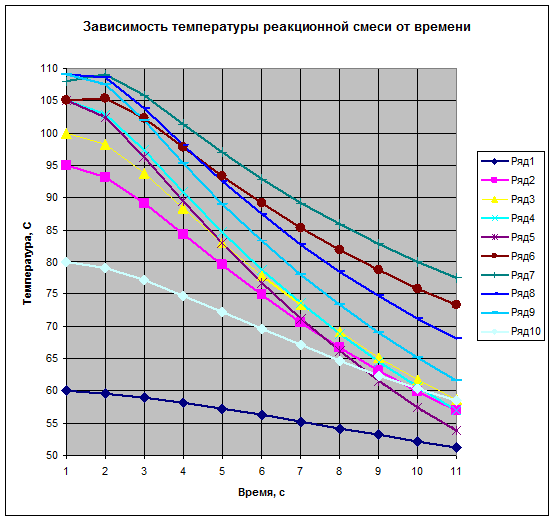

Примечание: около каждой точки обозначен номер соответствующего ей опыта и значение степени превращения, полученного в этом режиме.
Обсуждение результатов.
Таким образом, было смоделировано 10 различных режимов работы. В процессе выполнения работы температура реакционной смеси и стенки постепенно поднималась от минимальных значений к максимальным. В рассматриваемом реакторе протекает обратимая экзотермическая реакция, то есть реакция, протекающая с выделением тепла (Δ Н< 0). С точки зрения термодинамики, константа скорости прямой реакции в нашем случае будет падать с ростом температуры:
dlnk/dt = Δ H°/(RT2);
dlnk/dt < 0, k=f(T) ↓
Аналогично, в соответствии с принципом Ле-Шателье равновесие процесса смещается в сторону образования исходных веществ.
Рассмотрим систему с точки зрения разности энергий активации прямой и обратной реакции. Энергия активации есть минимальная энергия, которой должны обладать молекулы, чтобы их столкновение могло привести к химическому взаимодействию. Так как протекающая в системе реакция экзотермическая, энергия активации прямой реакции меньше, чем энергия активации обратной. Это видно из энергетической диаграммы:

Повышение температуры приводит к увеличению кинетической энергии всех частиц в системе, следовательно увеличивается число активных столкновений, увеличиваются скорости как прямой, так и обратной реакции. Зависимость скорости реакции от температуры выражается уравнением Аррениуса:
k = A*exp (-E/R*T)
k – константа скорости реакции; А – Предэкспоненциальный множитель; Е – энергия активации; R – универсальная газовая постоянная Т – температура.
Чем больше значение энергии активации, тем больше скорость реакции зависит от температуры. Так как а нашем случае Е2> Е1, с ростом температуры k2 растёт быстрее k1, следовательно скорость обратной реакции возрастает сильнее, чем прямой. Равновесие смещается в нежелательную сторону.
Скорость реакции также зависит от концентраций исходного вещества и продукта. Эта зависимость выражается кинетическими уравнениями:
r1= k1CA1
r2= k2CA2
Скорость прямой реакции тем выше, чем больше концентрация исходного компонента. Аналогично и для обратной реакции.
Рост выхода продукта при повышении температуры исходной смеси и при понижении температуры стенки можно объяснить следующим образом. В первые секунды реакции в системе ещё не накопилось большого количества продукта, скорость обратной реакции мала из-за малой концентрации продукта (скорость реакции определяет концентрация, а не температура). Когда в системе накопится достаточное количество продукта, скорость обратной реакции будет преобладать.
Вывод: пока еще не накопилось достаточное количество конечного продукта, процесс выгодно вести при высокой температуре, чтобы увеличить скорость прямой реакции, а затем температуру следует снижать, чтобы сместив равновесие в нужную сторону, добиться максимального выхода продукта.