
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ІІ. Поліпшена версія моделі
|
|
Припущення, використані нами у попередній версії, були занадто простими, тому й результати роботи з моделлю практично виявилися нецікавими. Перейдемо до вдосконалення моделі.
Згідно з Припущенням 4 наша модель передбачає однорідний за ознакою балакучості склад населення. У житті такого фактично не буває. Тому, насамперед, частково знімемо це обмеження і сформулюємо
Припущення 4 *. Будемо вважати, що населення складається з трьох груп: звичайних людей з параметром передавання kзв, балакунів з параметром передавання kб (kб > kзв) та мовчунів з параметром передавання kм = 0. При цьому, як і раніше, значення відповідних параметрів вважатимемо незмінними в часі.
Нехай доля мовчунів становить M, а балакунів – B від усієї кількості населення. Тоді доля звичайних знавців становитиме
Z = 1 – M – B.
Не викликатиме серйозних заперечень твердження, що за достатньо великої чисельності населення у такий самий спосіб розподіляються відповідні долі й серед знавців новини. Так, наприклад, якщо доля мовчунів серед усього населення становить М, то й серед знавців ця доля буде також М.
Тепер приріст Δ N кількості знавців після j -го передавання буде забезпечуватися балакунами та звичайними людьми і становитиме
 Δ N = Nj– 1 ·B·kб + Nj– 1 ·kзв· (1 – M – B) (4)
Δ N = Nj– 1 ·B·kб + Nj– 1 ·kзв· (1 – M – B) (4)
за рахунок за рахунок
балакунів звичайних
або
Δ N = Nj– 1(B·kб + kзв·Z); (5)
загальна ж кількість знавців шукатиметься, як і раніше згідно (2):
Nj = Nj– 1 + Δ N,
або з урахуванням (5)
Nj = Nj– 1(1 + B·kб+ kзв·Z), (5*)
Рівняння (5) і (2) або (5) і (5*) являють собою поліпшену математичну модель процесу.
Модифікована таблиця має такий вигляд:
| A | B | C | D | E | |
| j | Δ N | N | Дано: | ||
| M = | |||||
| B = | |||||
| kб = | |||||
| kзв = | |||||
| N 0 = | |||||
| … | … | … | … |
У відповідності до нових рівнянь потребує певних змін і
Алгоритм роботи з моделлю
– п. 2: до вхідних даних замість колишнього k добавити нові параметри M, B, Kб і kзв: (комірки Е2–Е5 відповідно), а параметр N 0 перенести до комірки Е6.
– п. 4.2: обчислювати приріст Δ N кількості знавців згідно (5):
| комірка | формула |
| B3 | = C2*($E$3*$E$4 +$ E$5*(1-$E$2-$E$3)) |
Значення параметрів М і В повинні задовольняти умові М+В £ 1, тому з метою хоч би часткового запобігання некоректного введення значень цих параметрів слід після заповнення комірок Е2 та Е3 в разі необхідності виводити на екран відповідне повідомлення. Для цього в комірці E8 слід створити формулу
=ЕСЛИ(E2+E3> 1; " Має бути М+В< =1! "; " ").
Решту пунктів алгоритму залишити без змін.
Обчислювальний експеримент
1. Вважатимемо, для прикладу, що за ознакою балакучості мешканці деякого населеного пункту розподіляються у такий спосіб: доля мовчунів М становить 0, 75 (75%), доля балакунів – 0, 1 (10%), решта Z = 1 – М – В – доля звичайних людей. Параметри передавання kб = 3, kзв = 2. Серед мешканців з’являється N 0 = 1 знавець чутки. Скільки людей знатимуть новину після n =22 сеансів передавання?
2. Вводимо дані й одержуємо відповідну таблицю (рис. 3.3).
| A | B | C | D | E | |
| j | D N | N | Дано: | ||
| M = | 0, 75 | ||||
| B = | 0, 1 | ||||
| kб = | |||||
| kзв = | |||||
| N 0 = | |||||
| ... | ... | ... | ... |
Рис. 3.3.
2.1. Чи утворює послідовність значень змінної Nj геометричну прогресію? Чому?
Якщо ваша відповідь негативна, то ви помиляєтесь. В оману вас увела саме несподіваність питання стосовно послідовності такого незвичного вигляду. По-перше, не слід забувати, що дійсні числа у комірках таблиці представлені у форматі цілих.
По-друге, погляньте на вираз (5*): з нього видно, що кожний наступний член Nj послідовності дорівнює попередньому Nj– 1, помноженому на постійне число q = 1 + kб·B + kзв·Z. Отже, послідовність
Nj -их – геометрична прогресія, а число q – її знаменник.
2.2. Напишіть формулу довільного члена утвореної послідовності у вигляді an = a 1 ·qn– 1. Для цього за нашими даними знайдіть конкретні значення N 1 (замість а 1), q і п.
2.3. Якого вигляду тепер набуде вираз для Nj?
2.4. Створіть у таблиці після стовпця значень N новий стовпець, у якому будуть обчислюватися значення Nj згідно виразу із п. 2.2:
Nj = N 1 · (1 + kб·B + kзв·Z) j– 1. (5)
Для цього в комірки D2 і D3 уведіть формули
| комірки | формули |
| D2 | = $F$6 |
| D3 | = $C$3*(1 + $F$3*$F$4 + $F$5*(1-$F$2-$F$3))^(A3-1) |
2.5. Порівняйте значення Nj у стовпцях C і D, зробіть висновки.
2.6. Переконатися, що послідовність Nj є дійсно геометричною прогресією, можна й інакше – виходячи з означення такої послідовності, а саме: відношення Nj / Nj – 1 має бути сталим числом.
То ж видаліть зі стовпця D попередні значення і в комірці D3 створіть відповідну формулу =С3/С2, яку скопіюйте у решту комірок стовпця D. Як слід прокоментувати той факт, що значення всіх комірок стовпця D виявляються однаковими?
Тепер стовпець D видаліть із таблиці.
3. З’ясуйте, як впливає на виведені значення Nj зміна параметрів М та В. З цією метою порівнюйте результати при початкових даних з результатами при
3.1. М = 0, 75 і В = 0, 05;
3.2. М = 0, 8 і В = 0, 1.
Прокоментуйте причини спостережуваних змін.
4. Поверніть параметрам М і В їхні початкові значення. Залишаючи їх незмінними, спробуйте одночасно підібрати для параметрів передавання kзв і kб такі нові значення, щоб у стовпці C залишилися попередні результати.
Коли вам набридне це заняття, введіть kзв = 1 і kб = 4, 5 (kб = 4, 5 можна інтерпретувати так: кожен балакун за два сеанси передавання знаходить 9 слухачів).
4.1. Звідки взялися ці числа 1 і 4, 5? Чи існують інші такі пари? Скільки їх може бути? Інакше кажучи, чи існує зв’язок між параметрами передавання kзв і kб за умовою п. 4?
На всі ці питання можна дати надійні відповіді, якщо знову звернутися до виразу (5*), який був переписаний у вигляді
Nj = Nj– 1 ·q,
де q = 1 +B·kб + kзв·Z.
Зрозуміло, що ті самі значення Nj будуть з’являтися кожного разу, коли будуть забезпечені однакові значення для q: q 1 = q 2, тобто
B·kб 1 + kзв 1 ·Z = B·kб 2 + kзв 2 ·Z.
Це рівняння одночасно містить обидві невідомі kб 2 і kзв 2. Розв’язуючи його, наприклад, відносно kб 2, маємо
 .
.
Беручи далі згідно умови М = 0, 75; В = 0, 1; кзв 1 = 2; кб 1 = 3, отримуємо
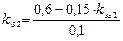 ,
,
або остаточно
kб 2 = 6 – 1, 5· kзв 2.
Тепер можна надавати певних значень кзв 2 і отримувати відповідні значення для кб 2. Необхідно лише контролювати себе очевидними обмеженнями кб 2 > 0, кзв 2 > 0, кб 2 > кзв 2.
Вправа
1. Дайте відповіді на питання п. 4.1.
2. Як і в п. 3 обчислювального експерименту попередньої версії моделі, створіть обмеження кількості знавців Nj так, щоб вона знов не перевищувала загальної чисельності S мешканців населеного пункту і порівняйте цю таблицю з таблицею попередньої версії.
3. За яких умов розглядувана версія моделі може бути зведена до попередньої?
Висновки
1. Поліпшена версія моделі є логічним продовженням попередньої і містить її як окремий випадок. Вона дещо цікавіша і більш реалістична, але все ще залишається дуже спрощеною і являє собою лише незначний крок уперед. Та й чого можна чекати від моделі, побудованої на обмеженій кількості зовсім простих припущень?
2. Пошук відповідей на питання, поставлені у п. 4 при виконанні обчислювального експерименту, мав на меті продемонструвати одну з важливих особливостей роботи дослідника у процесі моделювання. Суть її полягає в тому, що, виконуючи обчислювальний експеримент і аналізуючи його результати, можна, звичайно, пробувати шукати відповіді шляхом “сліпого” підбору, але значно ефективнішими завжди будуть спроби розв’язання проблеми шляхом аналізу математичних співвідношень, покладених в основу моделі. Проте, як ми побачимо далі, в моделюванні часто трапляються випадки, коли дослідник позбавлений такої можливості, і тоді залишається єдиний шлях – саме підбір.
3. Знов, як і у попередній версії моделі, поява обмеження чисельності знавців не робить модель більш вірогідною. Причина та сама – обмеження кількості знавців є штучним, воно зовсім не випливає із самої моделі.
4. В обох розглянутих версіях моделі найбільш слабким місцем є вимога, сформульована у Припущенні 3. Дійсно, хіба обов’язково чутка має потрапляти лише до тих осіб, яким вона невідома? Якщо цю вимогу зняти, то це означатиме, що слухачами можуть стати й ті особи, котрим чутка вже відома (повторні знавці). Тим більше, що у житті часто саме так і відбувається.