
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тригонометрические функции острого угла
|
|
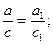 |  | 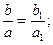 | 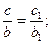 |
В прямоугольном треугольнике, имеющем данный угол a, отношения сторон не зависят от размеров треугольника. Рассмотрим два прямоугольных треугольника АВС и А1В1С1 (рис.1), имеющих равные углы Ð А=Ð А1 =a. Из подобия этих треугольников имеем:
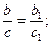 | 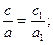 |
Если величину угла a измерить, то написанные равенства остаются справедливыми, а измениться
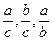

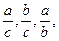 лишь числовое значение отношений и т.д. Поэтому отношения
лишь числовое значение отношений и т.д. Поэтому отношения
|
 | |||
 | |||
 | |||
 | |||
 |  | ||||||||
| |||||||||
| |||||||||
| |||||||||
 | |||
 | |||
Рис.1.
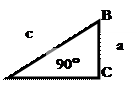
Синусом острого угла называется отношение противоположного этому углукатета к гипотенузе. Обозначают это так:
 |
sin a=
Значения тригонометрических функций (отношений отрезков) являются отвлеченными числами.
Приближенные значения тригонометрических функций острого угла можно найти непосредственно согласно их определениям. Построив прямоугольный треугольник с острым углом a и измерив его стороны, согласно определениям мы можемвычислить значение, например, sina.
Пользуясь тем, что значения тригонометрических функций не зависят от размеров треугольника, для вычисления значений sin углов a=30°; 45°; 60° рассмотрим прямоугольный треугольник с углом a=30°; и катетом ВС = a =1, тогда гипотенуза этого треугольника с =2, а второй катет b =Ö 3; рассмотрим также треугольник с углом a=45° и катетом a =1, тогда для этого треугольника c =Ö 2 и b =1.
Полученные результаты запишем в таблицу.
| 30° | 45° | 60° | |
| sina |
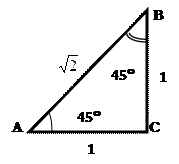 |
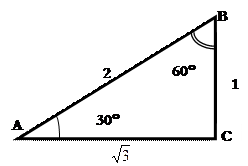 Рис.2.
Рис.2.
Приближенные значения тригонометрических функций для углов от 0° до 90° можно получить построив четверть круга, радиус которогопримем за 1, и его дугу разделимна 45 равных частей. Тогда градусная мера каждой части будет равна 2°.
N

0, 79
а
А b С 0, 62 0° M Рис.3.
Радиусы АМ и АN разделим на 100 равных частей. Построим прямоугольный треугольник с вершиной в центре круга и катетом совпадающим с радиусом АМ и гипотенузой АВ =1. Если угол ВАС =a, то по определению тригонометрических функций мы имеем:
sin a= а
Для угла 52° на шкале радиуса АN находим, что а =0, 79, а на шкале радиуса АМ находим, что b =0, 62., то есть sin 52°=0, 79.
Построив прямоугольные треугольники для углов a=2°, 4°, 6°, 8°, …, 88°, согласно рис.3., найдем значения (при аккуратных измерениях и вычислениях) с точностью до 0, 01. Для углов 0° и 90° прямоугольных треугольников не существует. Однако, если гипотенуза АВ будет стремиться по положению к радиусу АМ, то угол a®0, а катеты а ®0 и b ®1. В таком случае для полноты значений тригонометрических функций принимают, что
sin 0°= а =0; cos 0°= b =1.

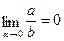
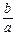
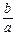
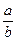 Что касается значений tg a и ctg a, то при a®0 отношение ®0, т.е., а отношение при a®0 неограниченно возрастает. Этот результат записывают как ®¥, где символ ¥ указывает, что величина неограниченно возрастает и не может быть выражена никаким числом, так как знак ¥ не является каким-либо числом. Таким образом, принимают, что tg 0°=0, а ctg 0° не существует, что чаще записывают как ctg 0°=¥.
Что касается значений tg a и ctg a, то при a®0 отношение ®0, т.е., а отношение при a®0 неограниченно возрастает. Этот результат записывают как ®¥, где символ ¥ указывает, что величина неограниченно возрастает и не может быть выражена никаким числом, так как знак ¥ не является каким-либо числом. Таким образом, принимают, что tg 0°=0, а ctg 0° не существует, что чаще записывают как ctg 0°=¥.
Рассуждая аналогично при a®90° приходим к целесообразности принять что
sin 90°=1; cos 90°=0, tg 90° не существует (tg 90°®¥) и ctg 90°=0.
Приведем таблицу значений синусов для углов от 0° до 90° с шагом 2°, которую можно получить указанным выше способом.
| градусы | ||||||||||||
| sin | 0, 00 | 0, 03 | 0, 07 | 0, 10 | 0, 14 | 0, 17 | 0, 21 | 0, 24 | 0, 28 | 0, 31 | 0, 34 | 0, 37 |
| градусы | ||||||||||||
| sin | 0, 41 | 0, 44 | 0, 47 | 0, 50 | 0, 53 | 0, 56 | 0, 59 | 0, 62 | 0, 64 | 0, 67 | 0, 69 | 0, 72 |
| градусы | ||||||||||||
| sin | 0, 74 | 0, 77 | 0, 79 | 0, 81 | 0, 83 | 0, 93 | 0, 87 | 0, 88 | 0, 90 | 0, 91 | 0, 93 | 0, 94 |
| градусы | ||||||||||||
| sin | 0, 95 | 0, 96 | 0, 97 | 0, 98 | 0, 98 | 0, 99 | 0, 99 | 1, 00 | 1, 00 | 1, 00 |
Пользуясь значениями тригонометрической функции y = sinx из таблицы, построим график.
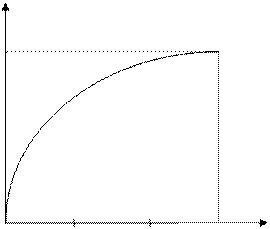 y
y
|
0 30° 60° 90° x
Рис.4.