
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение
|
|
Будем использовать разбиение множества учащихся класса на попарно непересекающиеся подмножества - классы с помощью трех свойств: " быть лыжником"; " быть пловцом" и " быть велосипедистом".
Получим 8 классов:
   лыжники пловцы
0 чел. 0 чел.
Х
0 чел.
Y
Z
0 чел.
велосипедисты
лыжники пловцы
0 чел. 0 чел.
Х
0 чел.
Y
Z
0 чел.
велосипедисты
|
Так как каждый спортсмен занимается только двумя видами спорта, устанавливаем, что численность четырех из восьми классов разбиения равна нулю (нет тех, кто занимается только лыжами, только плаванием, только велосипедом, и нет тех, кто одновременно занимается всеми тремя видами спорта).Численность же тех, кто составляет оставшиеся три класса спортсменов обозначим соответственно x, y, z. Далее, в соответствии с условием задачи, зная численность каждого из множеств, занимающихся лыжами, плаванием и велосипедом, получаем три уравнения:
x + z = 13
x + y = 8
y + z = 17
Сложим все уравнения и получим удвоенное число спортсменов: 2(x + y+ z)=38; значит всего спортсменов x + y+ z =19. Спортсмены учатся на " 3" или на " 4", следовательно, не являются отличниками, которых по условию в данном классе 6 человек. Всего в классе 25 человек, это и есть спортсмены и отличники, вместе взятые. Неуспевающих в этом классе, следовательно, нет.
Вариант 1.
1. Даны множества:
А = { yІ yÎ R, 3 ≤ y ≤ 9}; В ={ yІ yÎ Z, 2 < y < 10};
С = { y І yÎ N, y ≤ 9}
Изобразите их на числовой прямой и найдите А ∩ (В U С)и А\С.
2. Даны множества:
Е = ] -1; ∞ [ и М = [2; 9]. Найдите дополнения этих множеств до множества всех действительных чисел, пересечение дополнений.
3. Даны множества Р и К:
Найдите К ∩ Р, К U Р, К \ Р, Р \ К, если:
а) К = [2, 9 [, Р =[-1, 8];
б) К = [2, 9 ], Р =]-1, 8];
в) К = ]2, 9 [, Р =[-1, 8];
г) К = ]2, 9 ], Р =[-1, 8[.
4. Даны множества:
А= [-1, 4 ], В= ] 0, 6 ], С= [-3, 0], Д =] 1, 8]
Найдите: а)((А U С) ∩ В) U Д,
б)((А \ В) \ С) U Д,
в)(А ∩ В) \(С ∩ Д).
5. Начертите диаграмму Эйлера-Венна, если СÌ М, ЕÌ М,
С ∩ Е ¹ φ. Отметьте штриховкой множество 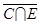 .
.
6.С помощью диаграммы Эйлера-Венна исследуйте вопрос о справедливости рассуждения:
Если А, В, С - подмножества универсального множества М такие, что 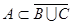 и
и 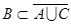 , то
, то 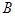 ¹ φ.
¹ φ.
7.Докажите справедливость равенства:
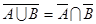
|
8. Проверьте правильность классификации:
четырехугольники делятся на параллелограммы, трапеции и прямоугольники.
9.Докажите, что пересечение множеств 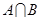 и
и 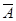
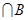 образует пустое множество.
образует пустое множество.
10. Анкетирование 100 студентов дало следующие результаты о количестве изучающих различные иностранные языки: английский язык изучают - 28 человек, немецкий - 30, французский -42, английский и немецкий - 8, английский и французский -10 человек, немецкий и французский - 5, все три языка одновременно изучают - 3 человека. Сколько студентов не изучают ни одного иностранного языка? Сколько студентов изучают один только французский язык? Сколько студентов изучают немецкий язык? -один английский? Сколько студентов изучают немецкий в том и только том случае, если они изучают французский?
Вариант 2.
1. Даны множества:
А = { x І x Î N, x > 3 }; В = { x І xÎ Z, x < 5 },
С = { x І xÎ R, 1 < x ≤ 7}
Изобразите их на числовой прямой и найдите (А ∩ В)\С и ВUС.
2. Даны множества:
Р= ] 0; 3 ] и К = [2; ∞ [.Найдите дополнения этих множеств до множества всех действительных чисел, объединение дополнений.
3. Даны множества В и С:
Найдите В ∩ С, В U С, В \ С, С \ В, если:
а) В = [0, 8 [, С =[-6, 10];
б) В = [0, 8 [, С =]-6, 10];
в) В = ]0, 8 [, С =[-6, 10];
г) В = ]0, 8 [, С =[-6, 10[.
4.Даны множества:
А= [1, 6], В= [2, 8], С= [-2, 3], Д= [1, 5]
Найдите: а)А U В U С U Д,
б)(А ∩ В) U (С ∩ Д),
в) ((А U В) ∩ С) U Д.
5. Начертите диаграмму Эйлера-Венна,
если Р ∩ К ∩ В ¹ φ. Отметьте штриховкой множество
К ∩ (Р U В).
6.С помощью диаграммы Эйлера-Венна обоснуйте утверждение: 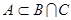 тогда и только тогда, когда
тогда и только тогда, когда 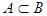 и
и 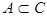 .
.
7.Докажите справедливость равенства:
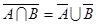
|
8. Проверьте правильность классификации:
целые неотрицательные числа делятся на составные и простые числа.
9.Докажите, что пересечение множеств  и
и 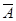
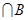 образует пустое множество.
образует пустое множество.
10. В лыжной, хоккейной и конькобежной секциях 38 человек. Известно, что в лыжной секции занимается 21 человек, среди которых 3 человека занимаются еще и в конькобежной секции, 6 человек еще в хоккейной секции и 1 человек занимается одновременно во всех трех секциях одновременно. В конькобежной секции занимаются 13 человек, среди которых 5 человек занимаются одновременно в двух секциях. Сколько человек в хоккейной секции?
Вариант 3.
1. Даны множества:
А = { yІ yÎ R, 2 < y ≤ 7}; В ={ yІ yÎ Z, 1 < y < 6};
С = { y І yÎ N, y ≤ 8}
Изобразите их на числовой прямой и найдите А U(В \ С)и В∩ С.
2. Даны множества:
О= ] 5; 13 ] и Н = [- ∞; 7 [.Найдите дополнения этих множеств до множества всех действительных чисел, объединение первого с дополнением второго.
3. Даны множества М и К:
Найдите М ∩ К, М U К, М \ К, К \ М, если:
а) М = [-2, 2 ], К =[-∞, 8];
б) М = [-2, 2 ], К =]-∞, 8];
в) М = ]-2, 2 [, К =[-∞, 8];
г) М = ]-2, 2 [, К =[-∞, 8[.
4. Даны множества:
А= [1, 3], В= ]2, 5], С= [3, 7[, Д= ]0, 4[.
Найдите: а)(А ∩ В) \ (С ∩ Д)
б) (А U В) \ (В U Д)
в)(А U Д)∩ (В U С).
5. Начертите диаграмму Эйлера-Венна, если
Р ∩ М ∩ О ¹ φ.Отметьте штриховкой множество
(М ∩ Р) U (М ∩ О).
6. С помощью диаграммы Эйлера-Венна обоснуйте утверждение:
Для того, чтобы 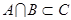 , необходимо и достаточно
, необходимо и достаточно 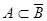
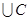 .
.
7.Докажите справедливость равенства:
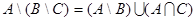
|
8. Проверьте правильность классификации:
натуральные числа делятся на четные, нечетные и кратные числу 3.
9.Докажите, что пересечение множеств  и
и 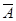
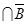
 образует пустое множество.
образует пустое множество.
10. Среди 150 школьников марки собирают только мальчики. Отечественные марки собирают 67 человек, марки Африки - 48 человек, марки Америки - 34 человека, только марки России - 11 человек, только Африки - 7, только Америки - " человека. Лишь один школьник собирает марки России, Африки и Америки. Сколько девочек среди 150 школьников?
Вариант 4.
1. Даны множества:
А = { x І x Î R, x > 13 }; В = { x І xÎ Z, x < 7 };
С = { x І xÎ N, 4 < x ≤ 12}
Изобразите их на числовой прямой и найдите А ∩ (В \ С)и В\А.
2. Даны множества:
В = ]-∞; 6 ] и П = [5; ∞ [.Найдите дополнения этих множеств до множества всех действительных чисел, пересечение первого с дополнением второго.
3. Даны множества О и Р:
Найдите О ∩ Р, О U Р, О \ Р, Р \ О, если:
а) О = [-3, ∞ [, Р =[-6, 8];
б) О = -3, ∞ [, Р =]-6, 8];
в) О = ]-3, ∞ [, Р =[-6, 8];
г) О = ]-3, ∞ [, Р =[-6, 8[.
4. Даны множества:
А= [2, 7[, В= [1, 8], С= [-1, 5[, Д= [0, 3].
Найдите: а) (А ∩ С) U (В \ Д)
б)((А ∩ Д)\С)U В
в)(А\(В U Д)) ∩ С.
5. Начертите диаграмму Эйлера -Венна, если
К ∩ М ∩ Е ¹ φ. Отметьте штриховкой множество
К U (М ∩ Е).
6.С помощью диаграммы Эйлера-Венна исследуйте вопрос о справедливости рассуждения:
Если А, В, С - подмножества множества М такие, что 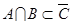 и
и  , то
, то  = φ.
= φ.
7.Докажите справедливость равенства:
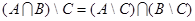
|
8.Проверьте правильность классификации:
треугольники делятся на разносторонние, равнобедренные и равносторонние.
9.Докажите, что объединение множеств 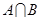 ,
,  ,
, 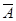
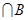 и
и 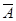
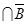 образует универсальное множество
образует универсальное множество 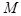 , подмножествами которого являются
, подмножествами которого являются  и
и 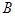 .
.
10. При обследовании 100 студентов были получены следующие данные о числе студентов, изучающих различные языки: только немецкий -18 человек; немецкий, но не испанский - 23; немецкий и французский - 8 человек; немецкий - 26; французский - 48; французский и испанский - 8; никакого иностранного языка - 24 человека. Сколько студентов изучают испанский язык? Сколько студентов изучают немецкий и испанский, но не французский?