
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Равносильные преобразования формул алгебры логики
|
|
Любую формулу алгебры логики можно преобразовать к равносильной ей, в которой используются только аксиоматически введенные операции: конъюнкция, дизъюнкция и отрицание.
Преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.). Логические операции обладают рядом свойств и подчинены логическим законам (см. табл.3).
Операции строгой дизъюнкции, импликации, эквиваленции, штрих Шеффера и стрелка Пирса могут быть равносильно выражены через операции конъюнкции, дизъюнкции и отрицания, поэтому они считаются как бы избыточными.
Логические равносильности алгебры логики:
a → b ≡ 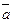 Ú b; Ú b;
|
aÅ b ≡ 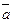 & bÚ a & & bÚ a & 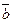 ; ;
|
a~b ≡ a & b Ú 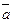 & & 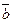 . .
|
| a | b ≡ Ø (a& b) |
| a ¯ b ≡ Ø (aÚ b) |
Равносильное упрощение формул выполняется по шагам:
1. замена операций импликации, строгой дизъюнкции, эквиваленции, функции Шеффера и стрелки Пирса логическими равносильностями;
2. применение законов алгебры логики.
Таблица 3. Свойства и законы алгебры логики
| Название | Содержание |
| Коммутативность (переместительный) | a Ú b ≡ bÚ a a & b ≡ b& a |
| aÅ b ≡ bÅ a | |
| Ассоциативность (сочетательный) | a Ú (b Ú c) ≡ (a Ú b) Ú с |
| a & (b & c) ≡ (a & b)& c | |
| aÅ (b Å c) ≡ (aÅ b) Å c | |
| Дистрибутивность (распределительный) | a & (b Ú c) ≡ (a & b)Ú (а & c) |
| a Ú (b & c) ≡ (a Ú b)& (а Ú c) | |
| Закон снятия двойного отрицания | 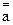 ≡ а ≡ а
|
| Законы де Моргана | 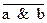 ≡ ≡ 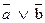
|
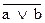 ≡ ≡ 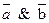
| |
| следствие закона | a Ú b ≡ 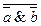 ;
a & b ≡ ;
a & b ≡ 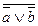
|
| Законы поглощения | a Ú a& b ≡ a a & (a Ú b) ≡ a |
| Свойства константы Л | aÚ Л ≡ a а & Л ≡ Л |
| Свойства константыИ | аÚ И≡ И а& И ≡ a |
| Закон исключения третьего | 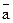 Ú a ≡ И Ú a ≡ И
|
| Законы идемпотентности | aÚ a ≡ a a& a ≡ a |
| Закон противоречия | 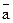 & a ≡ Л & a ≡ Л
|
| Законы склеивания | (a & b) Ú (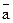 & b) ≡ b
(aÚ b) & ( & b) ≡ b
(aÚ b) & (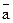 Ú b) ≡ b Ú b) ≡ b
|