Статистичні ознаки зображень поверхні металів

Ознаки концентрації для аналізу поверхні матеріалів

КЛАСИФІКАЦІЯ ПОВЕРХОНЬ МЕТАЛІВ

ЗА СТАТИСТИЧНИМИ ОЗНАКАМИ ЗОБРАЖЕННЯ

Дослідження текстур відіграє важливу роль для обробки зображень [1-6], зокрема для вивчення структурних особливостей оброблюваних поверхонь за допомогою статистичних методів, а саме: матриці кореляції [1], матриці відстаней [2], властивостей фракталів [3], розподілу ймовірностей реакцій фільтра [4], об’єднаного розподілу значень інтенсивності [5], просторового розподілу рівнів сірого [6]. Статистичні характеристики пов'язані з параметрами поверхні, і можуть використовуватися для їх класифікації. Окремі методи розроблені спеціально для класифікації текстур в загальному [3-4], або адаптовані конкретно до класифікації поверхонь матеріалу [5].

Також щоб оцінити якість поверхні матеріалу використовуються методи виявлення та класифікації дефектів [7].

Особливістю представленої роботи є порівняння простих статистичних ознак зображень на основі дисперсії при класифікації поверхонь різних металів.

Метою роботи є порівняння характеристик з точки зору придатності до класифікації поверхонь металу та дослідження умов їх застосування. Розрізнення і класифікації різних типів сплавів є умовою подальшої оцінки якості зразка, пошуку і класифікації дефектів матеріалу.

Статистичні ознаки зображень поверхні металів

При аналізі зображень поверхні металів слід враховувати їх особливості. По-перше, відмінності у структурі поверхні і якості її обробки добре помітні лише при збільшенні, тому в якості вхідних зображень доцільно використовувати зображення, отримані при зйомці під мікроскопом. По-друге, поверхні більшості металів (окрім, наприклад, золота чи міді) не сильно відрізняються за кольором. Тому для аналізу поверхні металу доцільно використовувати статистичні ознаки на основі інтенсивності у відтінках сірого. Крім того, алгоритми з використанням інтенсивності є більш універсальними, оскільки дозволяють ефективно працювати як з кольоровими, так і монохромними вхідними зображеннями.

Якщо вхідне зображення кольорове, то для отримання інтенсивності у відтінках сірого воно перетворюється. Кожен піксель приймає значення від чорного до білого кольору, яке позначимо як b – яскравість. Діапазон всіх можливих значень яскравості знаходиться в межах 0÷ 255. Для перетворення використовуємо алгоритм BT709 з наступними коефіцієнтами R, G, B:

R = 0, 2125; G = 0, 7154; B = 0, 0721; (1)

Як класифікаційні ознаки можуть використовуватись найпростіші статистичні характеристики, зокрема дисперсія [8, 9]. Для цього зображення ділиться на певні області, такі як стовпці і рядки [8], вертикальні і горизонтальні фрагменти [9], вертикальні і горизонтальні сегменти [9], комірки. Розподілена дисперсія характеризує дисперсію інтенсивності пікселів у кожній такій області зображення:

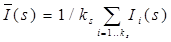(2а)

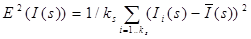(2б)

де 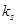– кількість пікселів у s -ій області зображення, 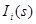– інтенсивність i -ого пікселя в s -ій області зображення, – математичне сподівання інтенсивності в s -ій області зображення, 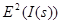– дисперсія інтенсивності пікселів в s -ій області зображення.

Розглянемо вказані способи обчислення розподіленої дисперсії:

1. Для обчислення розподіленої дисперсії по стовпцях вхідне зображення розбивається на X рівних за розміром стовпців, де X – ширина зображення в пікселях. Аналогічно зображення може бути розбите по рядках [8].

2. Для обчислення розподіленої дисперсії по вертикальних фрагментах вхідне зображення розбивається на n фрагментів вертикальними лініями з інтервалом (кроком фрагментації) d=X/n, де X – ширина зображення в пікселях. Аналогічно зображення може бути розбите по горизонтальних фрагментах [9]. При цьому, вертикальний фрагмент з інтервалом d=1 відповідає стовпцеві, а горизонтальний – рядку.

3. Для обчислення розподіленої дисперсії по сегментах кожен s -ий сегмент зображення формується об’єднанням всіх фрагментів від першого зліва до s -го включно [9]. Таким чином, перший сегмент відповідає першому фрагменту, а останній – цілому зображенню.

4. Для обчислення розподіленої дисперсії по комірках вхідне зображення розбивається на n частин вертикальними лініями і на m частин горизонтальними лініями, як при фрагментації. Після чого дисперсія обчислюється для кожної з n× m комірок.

Результатом, при будь-якому з цих чотирьох способів, є ряд значень дисперсії. А в якості загальних числових характеристик цілого зображення можуть бути використані такі характеристики:

1. Середнє значення дисперсій – обчислюється за формулою (2а), з підстановкою отриманого ряду значень дисперсії замість інтенсивності.

2. Дисперсія дисперсій – обчислюється за формулами (2), з підстановкою отриманого ряду значень дисперсії замість інтенсивності.

3. Амплітуда дисперсій – обчислюється як різниця максимального і мінімального елемента в отриманому ряді значень дисперсії.

Отже, при поєднанні 4 способів обчислення дисперсії і 3 загальних числових характеристик отримаємо 12 характеристик зображення на основі дисперсії.