Билинейные и квадратичные формы

Пусть над полем действительных чисел задано некоторое конечномерное линейное пространство L размерности n с фиксированным базисом .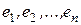

Определение 1. Функция f, определенная на L, называется линейной функцией, если 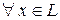ставится в соответствие действительное число 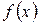, причем

1) ;

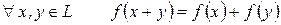2) 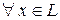и .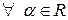

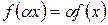Так как любой вектор 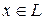может быть представлен в виде разложения по базису :

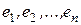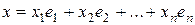, то

.

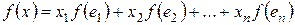Вводя,

;

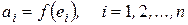получаем:

.

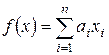Определение 2. Представление линейной функции 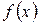в фиксированном базисе 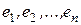в ви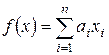де , где 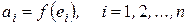, , 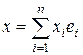называется линейной формой.

Как мы уже отметили выше, значения коэффициентов 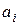и 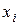, 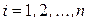зависят от выбора базиса в линейном пространстве L.

Определение 3. Функция двух переменных 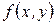, которая каждой паре 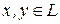ставит в соответствие действительное число 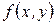, называется билинейной, если

1) , ;

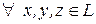
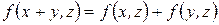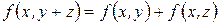2) 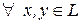и , .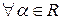

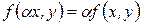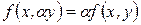Т. е. данная функция является линейной по каждому аргументу.

Учитывая возможность разложения векторов 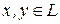по базису 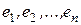, имеем:

,

.

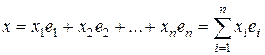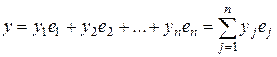Откуда следует, что

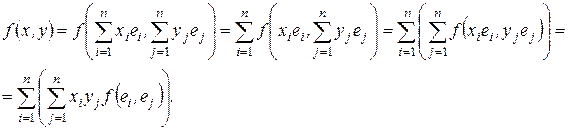
Вводя,

,

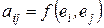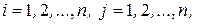
Получаем:

.

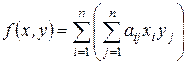Так как порядок суммирования в данном случае не имеет принципиального значения, то в литературе чаще всего данное выражение принято записывать более кратко:

.

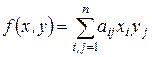Определение 4. Представление билинейной функции 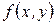в фиксированном базисе 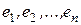в ви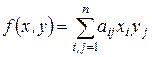де , где 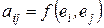, , 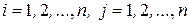, , 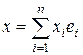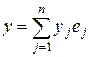называется билинейной формой.

Как уже было отмечено выше, значения коэффициентов, входящих в состав билинейной формы, зависят от выбора базиса в линейном пространстве.

Если ввести матрицы:

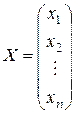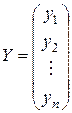, , , то

билинейная форма в рассматриваемом базисе может быть представлена в виде:

.
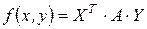