Действительно.

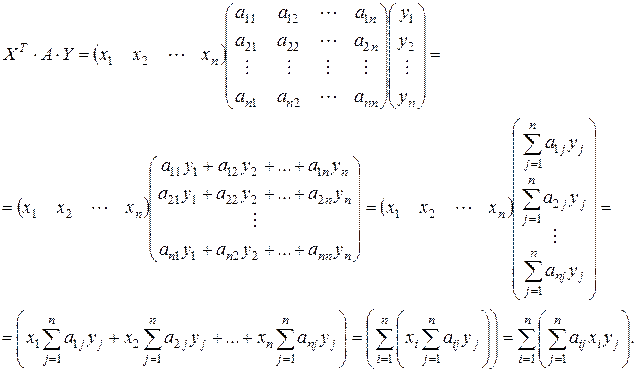
Определение 5. Матрица 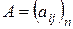, где 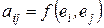, 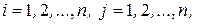называется матрицей билинейной формы в базисе .

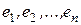Так как коэффициенты квадратичной формы зависят от выбора базиса, то матрица квадратичной формы при переходе к другому базису меняется.

Следовательно, в базисе 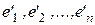квадратичная форма 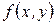будет иметь вид: 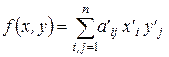, где , , , .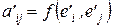

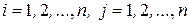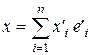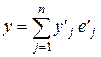В матричном ви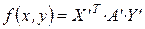де:

, где , , ,

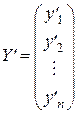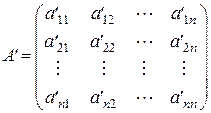Зная матрицу перехода 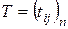от базиса 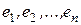к базису 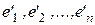, где 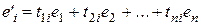, и, используя формулу связи координат одного и того же вектора в двух базисах одного и того же линейного пространства: 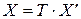нетрудно получить формулу для связи матриц квадратичной формулы в двух базисах.

1 способ (использование матричного представления):

, .

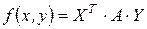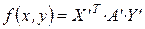Так как

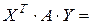
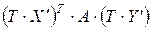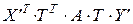= , то

.

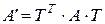2 способ (непосредственное вычисление элементов матрицы):

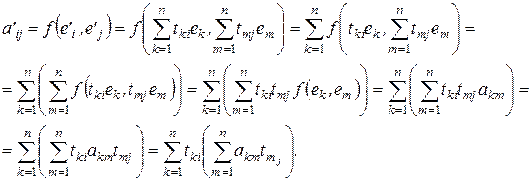
Нетрудно заметить, что 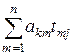элемент, стоящий на месте пересечения к -ой строки и j -го столбца произведения матриц A и Т, и, следовательно, 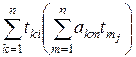- сумма произведений элементов i -ой строки матрицы 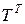и j -го столбца матрицы 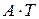, что и означает, что 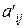- элемент произведения матриц 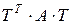, стоящий на пересечении i -ой строки и j -го столбца.

Так как матрица перехода Т – невырожденная матрица, то ранг матрицы билинейной формы не зависит от выбора базиса.

Определение 6. Ранг матрицы билинейной формы называется рангом билинейной формы.

Определение 7. Билинейная функция называется симметрической, если .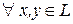

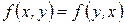В этом случае матрица соответствующей билинейной формы является симметрической и билинейная форма называется симметрической.

Теорема 1. Если в каком–нибудь базисе матрица билинейной формы симметрическая, то билинейная форма является симметрической.

Доказательство данной теоремы проведите самостоятельно.

Определение 8.. Билинейная функция называется кососимметрической, если .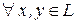

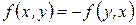В фиксированном базисе кососимметрическая функция представляется кососимметрической билинейной формой:

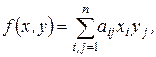где , ;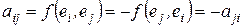

, .

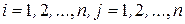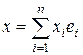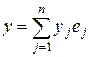Нетрудно заметить, что в этом случае .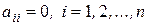

Теорема 2. Любая билинейная функция 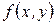может быть представлена в виде суммы симметрической и кососимметрической функций.