Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Доказательство. Нетрудно заметить, что для
|
|
Нетрудно заметить, что для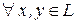 
,
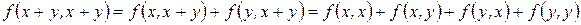Так как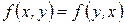 
, то 
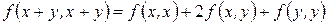и
. Утверждение доказано.
Опираясь на алгоритм представления билинейной формы в матричном виде в фиксированном базисе 
, учитывая, что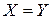 
, нетрудно получить представление квадратичной формы в матричном виде в том же базисе (проверьте самостоятельно):
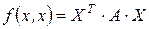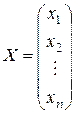, где 
, 
, где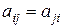 
,
, 
.
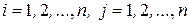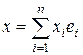При переходе к новому базису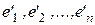 
квадратичная форма остается квадратичной формой и сохраняет вид своего матричного представления, изменяется лишь матрица квадратичной формы.
Пусть Т – матрица перехода от базиса к базису 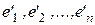, тогда, опираясь на формулу 
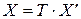связи координат одного и того же вектора х в двух базисах одного и того же линейного пространства, получаем:
,
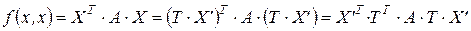следовательно, если ввести матрицу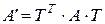 
, то в базисе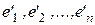
,
причем матрица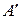 
остается симметрической:
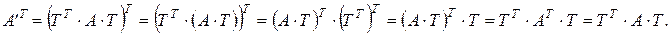
Таким образом, при переходе к новому базису квадратичная форма остается квадратичной формой относительно новых переменных и матрица квадратичной формы изменяется по закону: 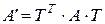, где Т – матрица перехода от старого базиса к новому базису. Так как Т – невырожденная матрица, то ранг матрицы квадратичной формы не изменяется.
Определение 10. Ранг матрицы квадратичной формы называется рангом квадратичной формы.
Определение 11. Если матрица А – невырожденная, то квадратичная форма называется невырожденной.
Отметим (без доказательства) несколько важных результатов, касающихся квадратичных форм, часто использующихся в приложениях.
Теорема 4. Для любой квадратичной формы 
можно указать базис, в котором эта квадратичная форма приводится к сумме квадратов: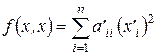 
(коэффициенты 
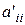могут принимать как положительные, так и отрицательные значения, так и обращаться в нуль).
Доказательство. (Смотрите в книге: Головина Л.И. Линейная алгебра и некоторые её приложения. – М: Наука, 1975, стр. 194 – 196.)
Теорема 5 (Закон инерции квадратичных форм). Если квадратичная форма приводится к сумме квадратов в двух различных базисах, то число положительных и отрицательных коэффициентов одинаково.
Доказательство. (Смотрите в книге: Головина Л.И. Линейная алгебра и некоторые её приложения. – М: Наука, 1975, стр. 197.)
Теорема 6. Если p - число положительных коэффициентов, а g - число отрицательных коэффициентов квадратичной формы, приведенной к сумме квадратов в некотором базисе, то 
, где r – ранг квадратичной формы.
Доказательство. (Смотрите в книге: Головина Л.И. Линейная алгебра и некоторые её приложения. – М: Наука, 1975, стр. 197.)
Определение 12. Разность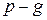 
называется сигнатурой квадратичной формы.
Определение 13. Квадратичная форма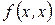 
называется положительно определенной, если 
.
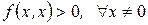Определение 14. Квадратичная форма 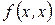называется отрицательно определенной, если 
.
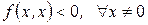Определение 15. Квадратичная форма 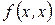называется положительно полуопределенной, если 
.
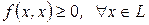Определение 16. Квадратичная форма 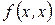называется отрицательно полуопределенной, если 
.
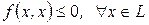Из указанных выше определений понятно, что положительно определенная квадратичная форма может быть приведена к сумме квадратов с положительными коэффициентами, а положительно полуопределенная к сумме квадратов с неотрицательными коэффициентами.
Теорема 7 (Критерий Сильвестра). Квадратичная форма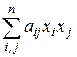 
положительно определенная тогда и только тогда, когда все угловые миноры матрицы 
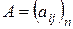- положительны, т.е.
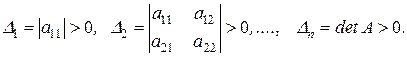
Доказательство. (Смотрите в книге: Головина Л.И. Линейная алгебра и некоторые её приложения. – М: Наука, 1975, стр. 198 - 200).
Следствие. Квадратичная форма 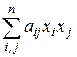является отрицательно определенной тогда и только тогда, когда знаки угловых миноров матрицы 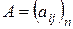чередуются, начиная со знака минус.
Теорема 8. Квадратичная форма 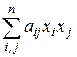может быть приведена к виду 
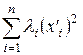, где 
- собственные значения матрицы 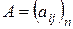квадратичной формы.
Доказательство. (Смотрите в книге: Головина Л.И. Линейная алгебра и некоторые её приложения. – М: Наука, 1975, стр. 201 – 203.).