
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Определение 4. Дополнительным минором к элементу определителя n-го порядка (1), называется определитель порядка
|
|
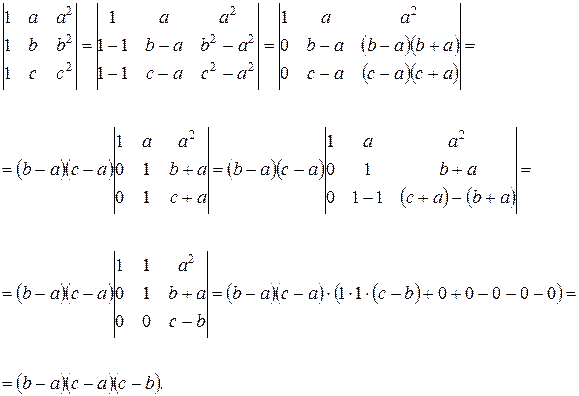
Тождество доказано.
Определение 4. Дополнительным минором к элементу 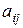 определителя n -го порядка (1), называется определитель порядка
определителя n -го порядка (1), называется определитель порядка  , получаемый из исходного, вычеркиванием i -й строки и j- го столбца.
, получаемый из исходного, вычеркиванием i -й строки и j- го столбца.
Обозначение:  .
.
Например, для определителя 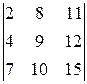 дополнительным минором к элементу
дополнительным минором к элементу 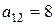 является определитель
является определитель 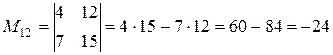 , а дополнительным минором к элементу
, а дополнительным минором к элементу 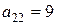 является определитель
является определитель  .
.
Определение 5. Алгебраическим дополнением к элементу 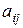 определителя n -го порядка (1), называется число, определяемое по правилу:
определителя n -го порядка (1), называется число, определяемое по правилу:  .
.
Обозначение: 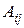 .
.
В частности, для определителя 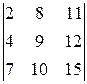 , рассмотренного выше, алгебраическим дополнением к элементу
, рассмотренного выше, алгебраическим дополнением к элементу 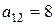 является число
является число 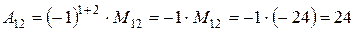 , а алгебраическим дополнением к элементу
, а алгебраическим дополнением к элементу 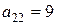 является число
является число 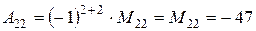 .
.
Теорема 10. Сумма произведений элементов любой строки определителя на алгебраические дополнения к ним равна величине определителя:
Доказательство. Проведите самостоятельно.
Следствие 8. Сумма произведений элементов любого столбца определителя на алгебраические дополнения к ним равна величине определителя:
Доказательство. Проведите самостоятельно.
Замечание. Теорема 10 и следствие 8 дают основное практическое правило для вычисления определителей порядка  , которое называется методом разложения по элементам строки или столбца определителя:
, которое называется методом разложения по элементам строки или столбца определителя:
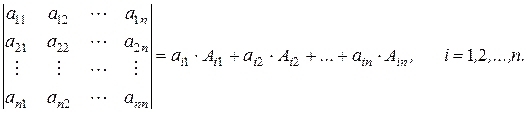 (10)
(10)
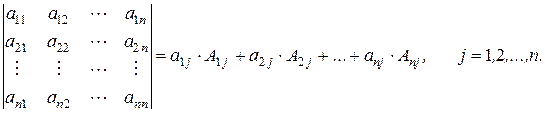 (11)
(11)
Пример 5. Вычислите определитель 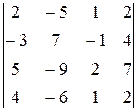 .
.
Решение.
1 способ. Воспользуется методом разложения по элементам первой строки.
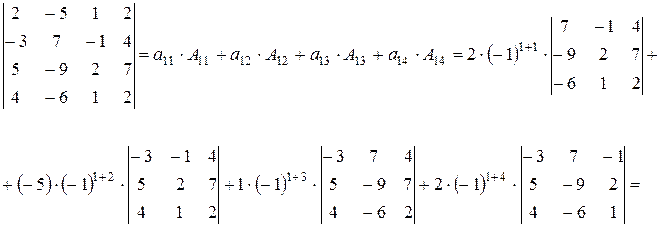
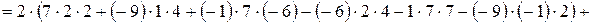

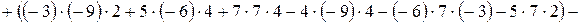


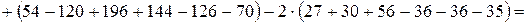
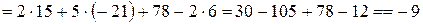 .
.
Очевидно, что выбор столбца или строки, по которым ведется разложение, в данном случае не имеет принципиального различия, так среди элементов нет нулевых, и при любом выборе расчет сведется к вычислению четырех определителей третьего порядка.
2 способ. Предварительно преобразуем исходный определитель, а точнее добьемся того, чтобы все элементы в третьем столбце за исключением одного оказались равными нулю. Для чего к элементам второй строки прибавим элементы первой строки, к элементам третьей строки прибавим элементы первой строки, умноженные на (-2) и затем к элементам четвертой строки прибавим элементы первой строки, умноженные на (-1). Согласно теореме 9 величина определителя при этом не изменится. Запишем расчеты, выполняя указанные действия последовательно.
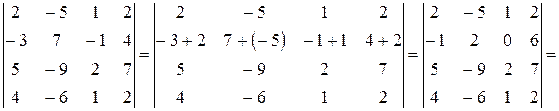
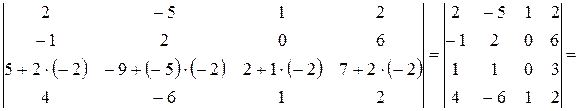
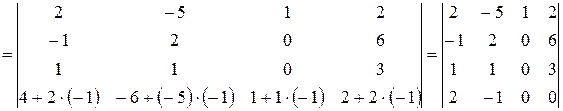
В получившемся определителе 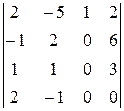 среди элементов третьего столбца только один отличен от нуля, поэтому для дальнейших расчетов разумно воспользоваться методом разложения по элементам третьего столбца.
среди элементов третьего столбца только один отличен от нуля, поэтому для дальнейших расчетов разумно воспользоваться методом разложения по элементам третьего столбца.

 .
.
Замечание. Правило вычисления определителей методом разложения по элементам строки или столбца позволяет получить особую формулу для вычисления определителей треугольного вида.