Пример 6.Вычислите определитель .

Решение.

.

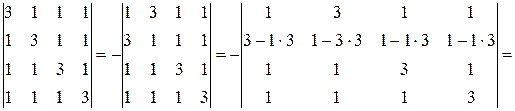
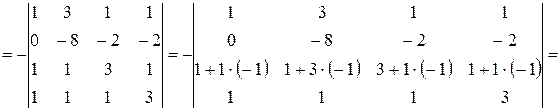
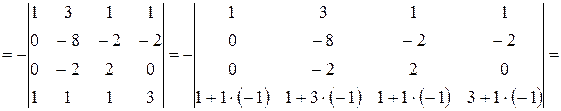
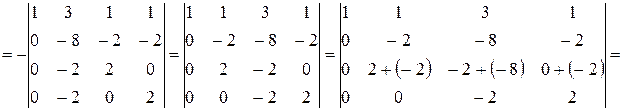
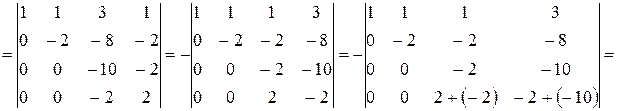
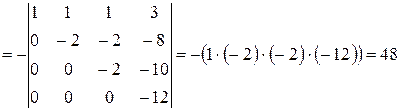Теорема 11. Сумма произведений элементов некоторой строки определителя на соответствующие алгебраические дополнения к элементам другой строки определителя равна нулю, т.е.

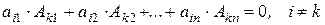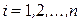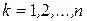, , . (13)

Доказательство. Рассмотрим определитель n- го порядка вида (1) и зафиксируем у него произвольным образом две строки i и k:

.

Составим новый определитель порядка n, заменяя все элементы k -ой строки соответствующими элементами i -ой строки:

.

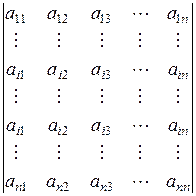Тогда, с одной стороны он равен нулю, как определитель, содержащий две одинаковые строки, с другой стороны, разлагая его по элементам к -ой строки, получаем, что его величина равна: 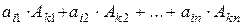, где 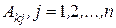- алгебраические дополнения к элементам к -ой исходного определителя. Это связано с тем, что данные опредлители отличаются только элементами k-ой строки, а вычисление алгебраических дополнений к элементам этой строки они не влияют. Таким образом, .

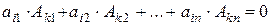В силу произвольности выбора строк результат будет справедлив для любых 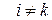, , 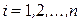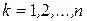. Теорема доказана.

Следствие 11. Сумма произведений элементов некоторого столбца определителя на соответствующие алгебраические дополнения к элементам другого столбца определителя равна нулю, т.е.

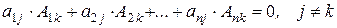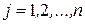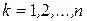, , . (14)

Доказательство. Проведите самостоятельно.

Теорема 12. Для любых квадратных матриц А и В одинакового порядка определитель произведения матриц равен произведению их определителей:

. (15).

Доказательство.

Покажем справедливость этого утверждения при .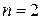

Пусть

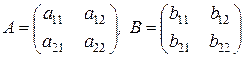, тогда .

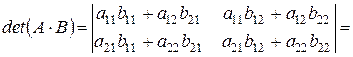
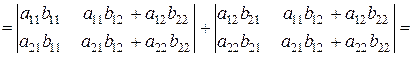
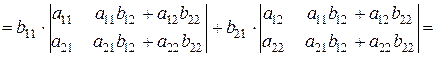
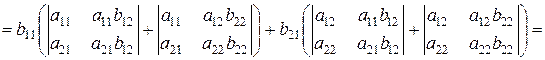
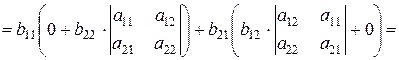
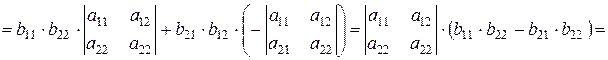
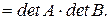Что и требовалось доказать. Справедливость утверждения в общем виде докажите самостоятельно.

Определение 6. Квадратная матрица, определитель которой отличен от нуля, называется невырожденной. В противном случае, т.е. если определитель матрицы равен нулю, она называется вырожденной.