
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейное пространство
|
|
Пусть задано множество L, элементами которогомогут быть как числа (числовые множества), так и другие объекты (векторы, матрицы, функции и т.д.). Элементы множества L будем обозначать 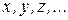 или
или 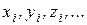 (в зависимости от ситуации).
(в зависимости от ситуации).
В зависимости от свойств элементов множества, операций, которые вводятся над элементами множества и свойствами этих операций, множества подразделяются на группы, кольца, поля, алгебры, линейные пространства и т.д. Мы остановимся на изучении множеств, которые называются линейными пространствами. С остальными типами множеств можно ознакомиться по учебнику А.Г. Курош «Курс высшей школы».
Пусть в множестве L введены две операции.
Операция сложения элементов множества, когда 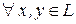 ставится в соответствие элемент единственный элемент
ставится в соответствие элемент единственный элемент 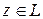 , называемый суммой элементов и обозначаемый
, называемый суммой элементов и обозначаемый 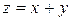 .
.
Операция умножения элементов множества на действительное (комплексное) число, когда 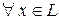 и
и 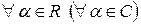 ставится в соответствие единственный элемент
ставится в соответствие единственный элемент 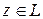 , называемый произведением х на действительное (комплексное) число
, называемый произведением х на действительное (комплексное) число 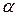 и обозначаемый
и обозначаемый 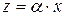 .
.
Определение 1. Множество L называется линейным пространством над полем действительных (комплексных) чисел, если операции сложения элементов и умножения на действительное (комплексное) число, обладают свойствами:
1) 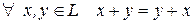 (коммутативность операции сложения);
(коммутативность операции сложения);
2) 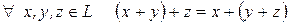 (ассоциативность операции сложения);
(ассоциативность операции сложения);
3) 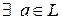 , такой что
, такой что 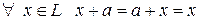 (элемент а называется нулевым и обозначается 0);
(элемент а называется нулевым и обозначается 0);
4) 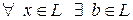 , такой что
, такой что 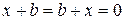 (элемент b называется противоположным элементу х и обозначается у = - х);
(элемент b называется противоположным элементу х и обозначается у = - х);
5) 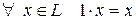 ;
;
6) 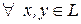 и
и 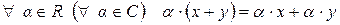 ;
;
7) 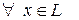 и
и 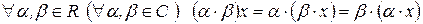 ;
;
8) 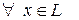 и
и 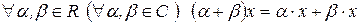 .
.
Замечание. Свойства 1) – 8) называются аксиомами линейного пространства.
Среди известных нам множеств, линейными пространствами являются, например:
· множество комплексных чисел (как над полем комплексных, так и над полем действительных чисел),
· множество действительных чисел (над полем действительных чисел);
· множество матриц размера 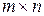 (над каким полем?);
(над каким полем?);
· множество векторов плоскости, исходящих из одной точки (над полем действительных чисел).
К множествам, не являющимся линейными пространствами, относятся, например:
· множество натуральных чисел;
· множество целых чисел;
· множество рациональных чисел.
Если множество L является линейным пространством, то из свойств 1) – 8) следует следующие интересные результаты, которые принято называть следствиями из аксиом.
Следствие 1. Если L – линейное пространство, то существует единственный нулевой элемент.
Доказательство. Применим метод от противного: предположим, что существуют два элемента 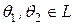 , такие что:
, такие что:
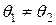 и
и  .
.
В этом случае получаем, что с одной стороны: 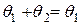 , так как
, так как 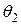 - нулевой элемент; а с другой стороны:
- нулевой элемент; а с другой стороны: 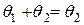 , так как
, так как 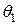 - нулевой элемент. Получаем противоречие. Следовательно, предположение – неверное, и
- нулевой элемент. Получаем противоречие. Следовательно, предположение – неверное, и 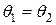 . Т. е. нулевой элемент – единственный.
. Т. е. нулевой элемент – единственный.
Следствие 2. Если L – линейное пространство, то 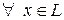 существует единственный противоположный элемент
существует единственный противоположный элемент 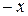 .
.
Доказательство. Применим метод от противного: предположим, что нашелся элемент 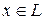 , для которого существуют два элемента
, для которого существуют два элемента 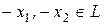 , такие что:
, такие что:
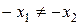 и
и 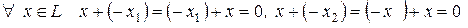 .
.
В этом случае получаем, что с одной стороны:
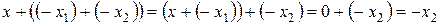 , так как
, так как 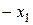 - элемент, противоположный элементу x; а с другой стороны:
- элемент, противоположный элементу x; а с другой стороны:
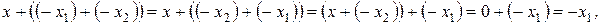 так как
так как 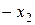 - элемент, противоположный элементу x. Получаем противоречие. Следовательно, предположение – неверное,
- элемент, противоположный элементу x. Получаем противоречие. Следовательно, предположение – неверное, 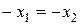 . Т. е. противоположный элемент – единственный.
. Т. е. противоположный элемент – единственный.