
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Доказательство. , откуда и следует, что является элементом, противоположным элементу .
|
|
1) 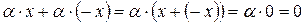 ,
,
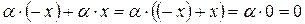 , откуда и следует, что
, откуда и следует, что 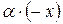 является элементом, противоположным элементу
является элементом, противоположным элементу 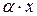 .
.
2) 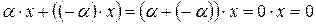 ,
,
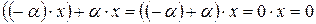 , откуда и следует, что
, откуда и следует, что 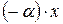 является элементом, противоположным элементу
является элементом, противоположным элементу 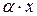 .
.
Определение 2. Элемент 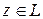 называется разностью элементов
называется разностью элементов 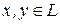 , если
, если 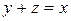 .
.
Обозначение: 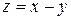 .
.
Следствие 7. 1) 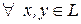 существует единственный элемент
существует единственный элемент 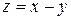 ;
;
2) 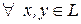 и
и 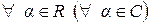
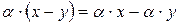 ;
;
3) 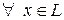 и
и 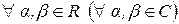
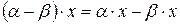 .
.
Доказательство. Доказательство проведите самостоятельно.
Вместо термина «линейное пространство» иногда употребляют термины «векторное пространство» или «аффинное пространство».
Элементы линейного пространства принято называть векторами.
Далее ограничимся рассмотрением линейных пространств над полем действительных чисел.
Пусть L - некоторое линейное пространство над полем действительных чисел. Пусть 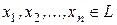 ,
, 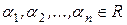 .
.
Определение 3. Выражение 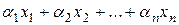 называется линейной комбинацией векторов
называется линейной комбинацией векторов 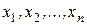 .
.
Определение 4. Набор коэффициентов 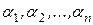 называется набором коэффициентов, соответствующим линейной комбинации векторов
называется набором коэффициентов, соответствующим линейной комбинации векторов 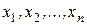 .
.
Определение 5. Набор коэффициентов 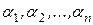 называется тривиальным (нулевым), если все коэффициенты равны нулю.
называется тривиальным (нулевым), если все коэффициенты равны нулю.
Определение 6. Набор коэффициентов 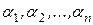 называется нетривиальным (ненулевым), если хотя бы один из коэффициентов отличен от нуля.
называется нетривиальным (ненулевым), если хотя бы один из коэффициентов отличен от нуля.
Определение 7. Векторы 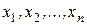 называются линейно зависимыми, если найдется нетривиальный набор коэффициентов
называются линейно зависимыми, если найдется нетривиальный набор коэффициентов 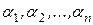 , при котором линейная комбинация векторов
, при котором линейная комбинация векторов 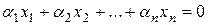 .
.
Иногда определение 7 дают чуть в ином виде.
Определение 7*. Система векторов 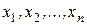 называется линейно зависимой, если найдется нетривиальный набор коэффициентов
называется линейно зависимой, если найдется нетривиальный набор коэффициентов 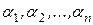 , при котором линейная комбинация векторов
, при котором линейная комбинация векторов 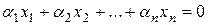 .
.
Определение 8. Векторы 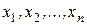 называются линейно независимыми, если линейная комбинация этих векторов обращается в нуль только при тривиальном наборе коэффициентов.
называются линейно независимыми, если линейная комбинация этих векторов обращается в нуль только при тривиальном наборе коэффициентов.
Определение 8*. Системавекторов 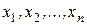 называется линейно независимой, если линейная комбинация этих векторов обращается в нуль только при тривиальном наборе коэффициентов.
называется линейно независимой, если линейная комбинация этих векторов обращается в нуль только при тривиальном наборе коэффициентов.
Замечание. Нетрудно заметить, что если набор (система) векторов 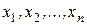 удовлетворяет определению 7 (7*), то не удовлетворяет определению 8 (8*), и наоборот. В связи с этим в некоторых учебниках ограничиваются только одним из этих определений.
удовлетворяет определению 7 (7*), то не удовлетворяет определению 8 (8*), и наоборот. В связи с этим в некоторых учебниках ограничиваются только одним из этих определений.
Теорема 1 (Критерий линейной зависимости векторов в произвольном пространстве) Векторы 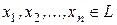 линейно зависимы тогда и только тогда, когда один из векторов является линейной комбинацией остальных, т.е.
линейно зависимы тогда и только тогда, когда один из векторов является линейной комбинацией остальных, т.е.
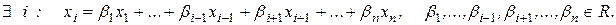 (Система векторов
(Система векторов 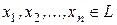 линейно зависима тогда и только тогда, когда один из векторов является линейной комбинацией остальных).
линейно зависима тогда и только тогда, когда один из векторов является линейной комбинацией остальных).