
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Доказательство.
|
|
1) Необходимость.
Пусть векторы 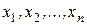 линейно зависимы, тогда существует нетривиальный набор коэффициентов
линейно зависимы, тогда существует нетривиальный набор коэффициентов 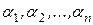 , при котором
, при котором 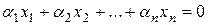 . Пусть
. Пусть 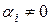 , тогда
, тогда
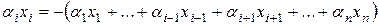 ,
,
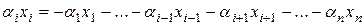 ,
,
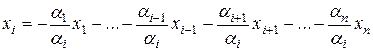 .
.
Вводя 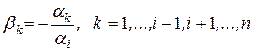 , получаем результат:
, получаем результат:
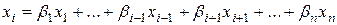 ,
,
который и требовалось доказать.
2) Достаточность. Пусть
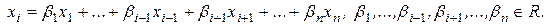
Тогда
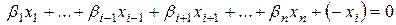 ,
,
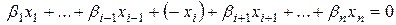 ,
,
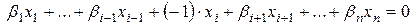 .
.
Откуда следует, что линейная комбинация векторов 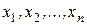 обращается в нуль при нетривиальном наборе коэффициентов
обращается в нуль при нетривиальном наборе коэффициентов 
 , где
, где 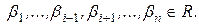
Следовательно, векторы 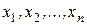 - линейно зависимы, что и требовалось доказать.
- линейно зависимы, что и требовалось доказать.
Следствие 1. Если среди векторов 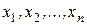 имеется нулевой вектор, то они линейно зависимы. (Если система векторов содержит нулевой вектор, то она линейно зависимая).
имеется нулевой вектор, то они линейно зависимы. (Если система векторов содержит нулевой вектор, то она линейно зависимая).
Доказательство. Пусть 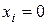 , тогда при наборе коэффициентов:
, тогда при наборе коэффициентов:
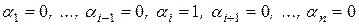 , получаем, что
, получаем, что
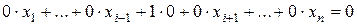 .
.
Следствие 2. Если среди векторов 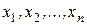 есть два равных вектора, то они линейно зависимы. (Если система векторов содержит два равных вектора, то она линейно зависимая).
есть два равных вектора, то они линейно зависимы. (Если система векторов содержит два равных вектора, то она линейно зависимая).
Доказательство. Пусть 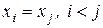 . Тогда, при
. Тогда, при
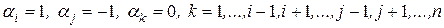 линейная комбинация векторов
линейная комбинация векторов 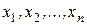 обратится в нуль.
обратится в нуль.
Следствие 3. Если среди векторов 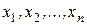 есть два противоположных вектора, то они линейно зависимы. (Если система векторов содержит два противоположных вектора, то она линейно зависимая).
есть два противоположных вектора, то они линейно зависимы. (Если система векторов содержит два противоположных вектора, то она линейно зависимая).
Доказательство. Пусть 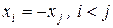 . Тогда, при
. Тогда, при
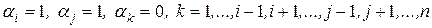 линейная комбинация векторов
линейная комбинация векторов 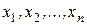 обратится в нуль.
обратится в нуль.
Следствие 4. Если среди векторов 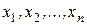 есть к линейно зависимых, то они линейно зависимы. (Если система векторов содержит линейно зависимую подсистему векторов, то она линейно зависимая).
есть к линейно зависимых, то они линейно зависимы. (Если система векторов содержит линейно зависимую подсистему векторов, то она линейно зависимая).
Доказательство. Пусть линейно зависимыми являются векторы 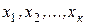 ,
, 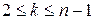 (в случае необходимости векторы всегда можно перенумеровать). Тогда существует нетривиальный набор коэффициентов
(в случае необходимости векторы всегда можно перенумеровать). Тогда существует нетривиальный набор коэффициентов 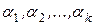 , при котором
, при котором 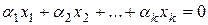 .
.
Полагая 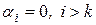 , получаем, что
, получаем, что
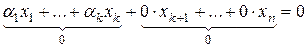 .
.
Следствие 5. Если векторы 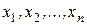 линейно независимые, то любые к векторов из этого набора являются линейно независимыми. (Если система векторов линейно независимая, то любая её подсистема векторов линейно независима).
линейно независимые, то любые к векторов из этого набора являются линейно независимыми. (Если система векторов линейно независимая, то любая её подсистема векторов линейно независима).
Доказательство. Применим метод от противного. Предположим, что нашлась линейно зависимая подсистема векторов, тогда, согласно следствию 4, вся система векторов будет линейно зависимой. Получаем противоречие. Следовательно, предположение является неверным, и любая подсистема векторов будет линейно независимой.
Замечание. Из полученных выше результатов, опираясь на знания школьной программы, в частности, можно сделать следующие выводы.
В линейном пространстве векторов, исходящих из одной точки на плоскости: 1) любые два коллинеарных вектора – линейно зависимы, а любые два неколлинеарных вектора линейно независимы; 2) любые три вектора – линейно зависимы.
В линейном пространстве векторов, исходящих из одной точки в «реальном» пространстве: 1) любые три компланарных вектора линейно зависимы, а любые три некомпланарных вектора линейно независимы; 2) любые четыре вектора – линейно зависимы.
Определение 9. Линейное пространство L называется конечномерным, размерности n, если в этом пространстве найдется система из n линейно независимых векторов, а любая система из n+1 вектора уже линейно зависима.
Обозначение: 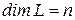 .
.
Определение 10. Линейное пространство L называется бесконечномерным, если 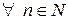 в нем найдется система из n линейно независимых векторов.
в нем найдется система из n линейно независимых векторов.
Обозначение: 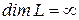 .
.
Определение 11. Система векторов называется базисом линейного пространства L, если
1) она линейно независима;
2) любой вектор 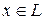 может быть представлен в виде линейной комбинации этих векторов.
может быть представлен в виде линейной комбинации этих векторов.
Теорема 2 (О способе выбора базиса в конечномерном пространстве). Если L - конечномерное линейное пространство размерности n, то любая система из n линейно независимых векторов является базисом этого пространства.
Доказательство. Пусть 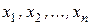 - произвольная линейно независимая система векторов линейного пространства L. Она является базисом, если удовлетворяет условиям определения 11. Условие 1 данного определения выполняется автоматически, так как данная система векторов по способу выбора является линейно независимой. Следовательно, остается доказать выполнение второго условия.
- произвольная линейно независимая система векторов линейного пространства L. Она является базисом, если удовлетворяет условиям определения 11. Условие 1 данного определения выполняется автоматически, так как данная система векторов по способу выбора является линейно независимой. Следовательно, остается доказать выполнение второго условия.
Пусть x - произвольный вектор линейного пространства L. Так как 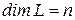 , то любая система из n +1 вектора будет линейно зависимой, следовательно, система векторов
, то любая система из n +1 вектора будет линейно зависимой, следовательно, система векторов 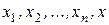 уже линейно зависимая. Это означает, что найдется нетривиальный набор коэффициентов
уже линейно зависимая. Это означает, что найдется нетривиальный набор коэффициентов 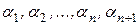 , при котором
, при котором
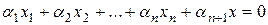 .
.
Покажем, что коэффициент 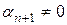 . Это легко доказать методом от противного. Предположим, что
. Это легко доказать методом от противного. Предположим, что 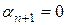 , тогда
, тогда
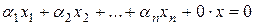 ,
,
откуда следует, что
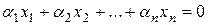 .
.
Так как в случае равенства нулю коэффициента 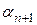 , набор коэффициентов
, набор коэффициентов 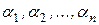 является нетривиальным, то векторы
является нетривиальным, то векторы 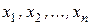 - линейно зависимы. Получаем противоречие, так как по способу выбора, осуществленного ранее, векторы
- линейно зависимы. Получаем противоречие, так как по способу выбора, осуществленного ранее, векторы 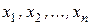 линейно независимые. Следовательно, выдвинутое предположение является неверным, и
линейно независимые. Следовательно, выдвинутое предположение является неверным, и 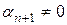 . В таком случае имеем:
. В таком случае имеем:
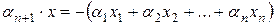 ,
,
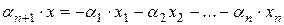 ,
,
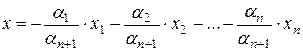 ,
,
т.е. вектор x является линейной комбинацией векторов 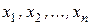 .
.
В силу произвольности выбора вектора x результат будет справедлив для любого вектора 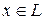 . Следовательно, выбранная система векторов
. Следовательно, выбранная система векторов 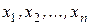 является базисом. В силу произвольности выбора линейно независимой системы из n векторов результат будет справедлив для любой системы из n линейно независимой системы векторов. Теорема доказана.
является базисом. В силу произвольности выбора линейно независимой системы из n векторов результат будет справедлив для любой системы из n линейно независимой системы векторов. Теорема доказана.
Замечание. В частности, опираясь, на сделанные выше замечания, и доказанную теорему, можно отметить, что линейное пространство векторов плоскости, исходящих из одной точки – есть конечномерное пространство размерности 2, где в качестве базиса можно выбрать любые два неколлинеарных вектора; линейное пространство векторов, исходящих из одной точки в «реальном» пространстве – есть конечномерное пространство размерности 3, где в качестве базиса можно выбрать любые три некомпланарных вектора.
Следствие. В конечномерном линейном пространстве L, размерности n, любая система из 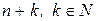 векторов является линейно зависимой.
векторов является линейно зависимой.
Доказательство. Если 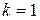 , то линейная зависимость системы из
, то линейная зависимость системы из 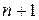 вектора автоматически следует из определения 9, так как
вектора автоматически следует из определения 9, так как 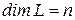 . При
. При 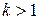 система из
система из 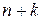 векторов содержит
векторов содержит 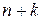 различных подсистем из
различных подсистем из 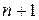 вектора, каждая из которых является линейно зависимой, а, следовательно, и сама система является линейно зависимой (смотрите следствие 4 к теореме 1).
вектора, каждая из которых является линейно зависимой, а, следовательно, и сама система является линейно зависимой (смотрите следствие 4 к теореме 1).
Иногда определение базиса дают иначе.
Определение 12. Базисом линейного пространства L называется максимально линейно независимая система векторов.
Очевидно, что определения 11 и 12 являются эквивалентными. Т.е. система векторов, являющаяся базисом по определению 11, является базисом и по определению 12, и наоборот.
Базис конечномерного линейного пространства размерности принято обозначать 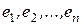 . Очевидно, что в линейном пространстве базис можно выбрать неединственным образом.
. Очевидно, что в линейном пространстве базис можно выбрать неединственным образом.
Определение 13. Представление вектора 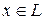 в виде
в виде 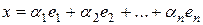 называется разложением по базису. Набор коэффициентов
называется разложением по базису. Набор коэффициентов 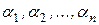 в этом случае называется координатами вектора х в базисе
в этом случае называется координатами вектора х в базисе  .
.
Теорема 3 (О единственности разложения вектора по базису). Если в конечномерном линейном пространстве L, размерности n, зафиксирован базис  , то для любого вектора
, то для любого вектора 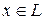 найдется единственный набор коэффициентов
найдется единственный набор коэффициентов 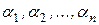 , такой что
, такой что 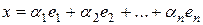 .
.
Доказательство. Применим метод от противного. Предположим, что в линейном пространстве L найдется вектор х, для которого возможны два разложения. Т.е. существуют два различных набора 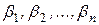
 и
и 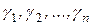 ; такие, что:
; такие, что:
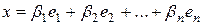 и
и 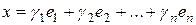 .
.
Тогда,
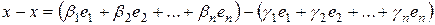 ,
,
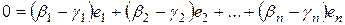 .
.
Так как векторы  образуют базис, то они линейно независимые. Следовательно, их линейная комбинация может обратиться в нуль только при тривиальном наборе коэффициентов, откуда следует, что:
образуют базис, то они линейно независимые. Следовательно, их линейная комбинация может обратиться в нуль только при тривиальном наборе коэффициентов, откуда следует, что:

Получаем противоречие с выдвинутым предположением, следовательно, оно – неверное и разложение по базису – единственное. Теорема доказана.
Замечание. Очевидно, что в различных базисах одного и того же линейного пространства L координаты вектора различны. Ниже будут рассмотрены формулы связи координат одного и того же вектора в двух базисах одного и того же пространства.
Теорема 4 (Критерий линейной независимости векторов в конечномерном пространстве). Если 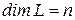 ,
,  - базис, то векторы
- базис, то векторы
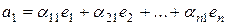 ,
,
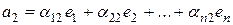 ,
,
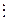
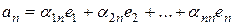
линейно независимы тогда и только тогда, когда
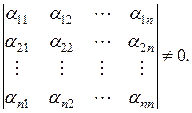
Доказательство. Заметим, что 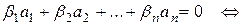
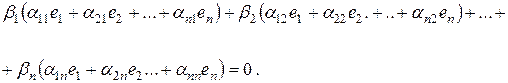
Перегруппировав слагаемые, и выделив коэффициенты при базисных векторах  , получаем:
, получаем:
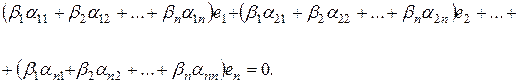
Так как базисные векторы  – линейно независимые векторы, то линейная комбинация этих векторов обращается в нуль только при тривиальном наборе коэффициентов, следовательно,
– линейно независимые векторы, то линейная комбинация этих векторов обращается в нуль только при тривиальном наборе коэффициентов, следовательно,
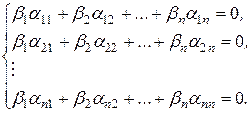
Получившаяся система является линейной однородной системой с постоянными коэффициентами, неизвестными в которой являются 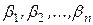 .
.
Согласно следствию из правила Крамера, данная система имеет нетривиальное решение (тогда векторы 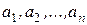 являются линейно зависимыми), тогда и только тогда, когда определитель, составленный из коэффициентов при неизвестных равен нулю. И, соответственно, имеет только тривиальное решение (тогда векторы
являются линейно зависимыми), тогда и только тогда, когда определитель, составленный из коэффициентов при неизвестных равен нулю. И, соответственно, имеет только тривиальное решение (тогда векторы 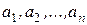 являются линейно независимыми), тогда и только тогда, когда определитель, составленный из коэффициентов при неизвестных, отличен от нуля.
являются линейно независимыми), тогда и только тогда, когда определитель, составленный из коэффициентов при неизвестных, отличен от нуля.
Следовательно, векторы 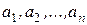 линейно независимы тогда и только тогда, когда
линейно независимы тогда и только тогда, когда 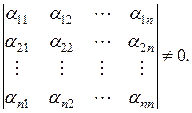 Теорема доказана.
Теорема доказана.
Следствие (Критерий линейной зависимости векторов в конечномерном пространстве) Если 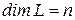 ,
,  - базис, то векторы
- базис, то векторы
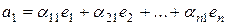 ,
,
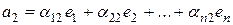 ,
,
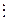
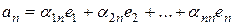
линейно зависимы тогда и только тогда, когда
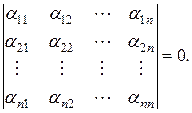
Доказательство. Данный результат автоматически получен при доказательстве рассмотренной выше теоремы.
Теперь выведем формулы для связи двух базисов одного и того же конечномерного линейного пространства L, размерности n.
Пусть в пространстве L заданы два базиса  и
и 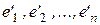 . Их, как правило, называют «старый» и «новый». Пусть известны координаты векторов нового базиса
. Их, как правило, называют «старый» и «новый». Пусть известны координаты векторов нового базиса 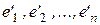 в старом:
в старом:
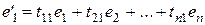 ,
,
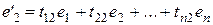 ,
,
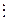
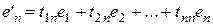 .
.
Если ввести матрицы
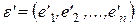 ,
, 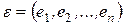 ,
, 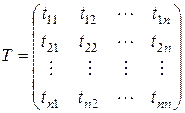 ,
,
то связь между векторами базисов можно представить в матричном виде:
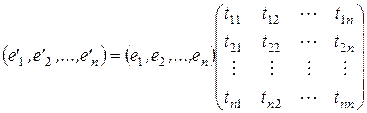
или кратко
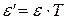 .
.
Получившаяся формула называется формулой перехода от «старого» базиса  к «новому» базису
к «новому» базису 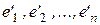 .
.
Матрица 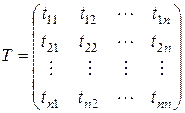 называется матрицей перехода от базиса
называется матрицей перехода от базиса  к базису
к базису 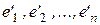 . Её столбцы – координаты новых базисных векторов в старом.
. Её столбцы – координаты новых базисных векторов в старом.
Так как базис 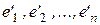 состоит из линейно независимых векторов, то согласно теореме 4,
состоит из линейно независимых векторов, то согласно теореме 4, 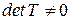 , т.е. матрица перехода является невырожденной.
, т.е. матрица перехода является невырожденной.
В таком случае для неё существует обратная матрица 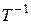 . Умножая обе части полученного выше равенства на
. Умножая обе части полученного выше равенства на 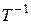 справа, получаем:
справа, получаем:
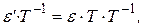
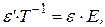
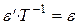 .
.
Получившаяся формула называется формулой перехода от «нового» базиса 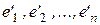 к старому базису
к старому базису  .
.
Зная связь между двумя базисами  и
и 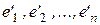 конечномерного линейного пространства L размерности n, легко получить формулы для связи координат любого вектора
конечномерного линейного пространства L размерности n, легко получить формулы для связи координат любого вектора 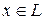 в этих базисах.
в этих базисах.
Пусть в базисе 
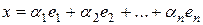 , а в базисе
, а в базисе 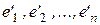
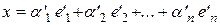 .
.
Вводя матрицы  и
и 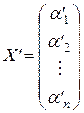 ,
,  разложение вектора х по базисам
разложение вектора х по базисам  и
и 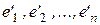 можно представить в матричном виде:
можно представить в матричном виде:
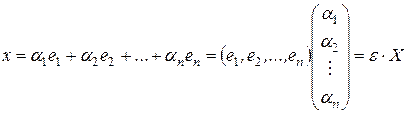 ,
,
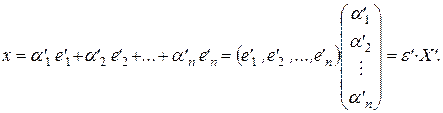
Откуда следует, что
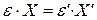 .
.
Учитывая связь между базисами: 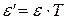 , где Т – матрица перехода от базиса
, где Т – матрица перехода от базиса  к базису
к базису 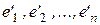 , получаем.
, получаем.
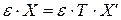 .
.
В силу единственности разложения вектора по базису:
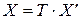 .
.
Получившаяся формула называется формулой перехода от координат вектора x в базисе 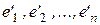 к координатам вектора x в базисе
к координатам вектора x в базисе  , где Т – матрица перехода от базиса
, где Т – матрица перехода от базиса  к базису
к базису 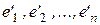
Формула перехода от координат вектора x в базисе  к координатам вектора х в базисе
к координатам вектора х в базисе 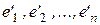 , когда известна матрица перехода Т от базиса
, когда известна матрица перехода Т от базиса  к базису
к базису 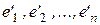 , может быть выведена двумя способами.
, может быть выведена двумя способами.
1 способ. На основе полученной выше формулы перехода от координат вектора x в базисе 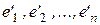 к координатам вектора x в базисе
к координатам вектора x в базисе  .
.
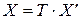 .
.
Так как матрица перехода Т – невырожденная матрица, то у неё существует обратная матрица 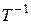 . Умножая обе части поучившегося равенства на
. Умножая обе части поучившегося равенства на 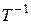 получаем:
получаем:
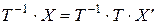 ,
,
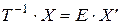 ,
,
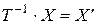 .
.
2 способ. На основе формулы перехода от базиса 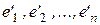 к базису
к базису  .
.
Как уже было отмечено выше:
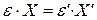 ,
,
так как
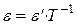 ,
,
где Т – матрица перехода от «старого» базиса  к новому базису
к новому базису 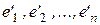 , то
, то
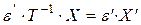 .
.
Из единственности разложения вектора х по базису 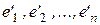 получаем нужный результат:
получаем нужный результат:
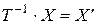 .
.
Данная формула называется формулой перехода от координат вектора х в базисе  к координатам вектора х в базисе
к координатам вектора х в базисе 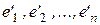 .
.
Замечание. В некоторых учебниках вместо матриц-строк 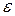 и
и 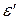 рассматривают матрицы- столбцы, а вместо матриц- столбцов X и X’ рассматривают матрицы- строки. В этом случае иначе составляется и матрица перехода: координаты новых базисных векторов – строки матрицы, и формулы связи базисов и координат вектора в этих базисах изменяют свой вид. Для того, чтобы в дальнейшем не произошло путаницы, данные формулы в нашем курсе не приводятся.
рассматривают матрицы- столбцы, а вместо матриц- столбцов X и X’ рассматривают матрицы- строки. В этом случае иначе составляется и матрица перехода: координаты новых базисных векторов – строки матрицы, и формулы связи базисов и координат вектора в этих базисах изменяют свой вид. Для того, чтобы в дальнейшем не произошло путаницы, данные формулы в нашем курсе не приводятся.