Марковские случайные процессы. Определения.

МАРКОВСКИЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ - процессы без вероятностного последствия, статистич. свойства к-рых в последующие моменты времени зависят только от значений процессов в данный момент и не зависят от их предыстории. M.с.п. - удобная матем. идеализация разл. случайных процессов, встречающихся в физике. К ним относятся процессы типа броуновского движения, равновесные и неравновесные флуктуации параметров макроскопич. систем, сравнительно медленные изменения амплитуды и фазы сигналов автогенераторов под действием быстро меняющихся естеств. шумов и т. д. Эффективность марковского процесса приближения при рассмотрении реальных случайных процессов обусловлена существованием развитого матем. аппарата для анализа статистич. свойств M.с.п.

Тип M.с.п. X(t)определяется тем, к какому множеству принадлежат аргумент t и возможные значения процесса х. Если t и х принимают дискретные значения, X(t)представляет собой марковскую цепь. M.с.п. с непрерывным временем, принимающий значения из дискретного множества 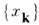, наз. дискретнозначным марковским процессом. К ним относится, в частности, телеграфный процесс с двумя значениями 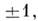смена к-рых происходит в случайные моменты времени.

Рассмотрим непрерывнозначный M.с.п. с непрерывным временем. Пусть в моменты 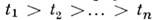известны значения процесса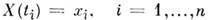

и 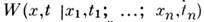- условная плотность вероятности значений процесса в момент t > t\, тогда справедливо равенство

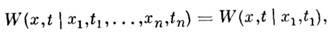
выражающее отсутствие последействия. Условную плотность вероятности 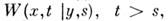полностью определяющую [вместе с безусловной плотностью вероятности 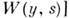все статистич. свойства M.с.п., наз. плотностью вероятности переходов. Она удовлетворяет интегральному уравнению Смолуховского

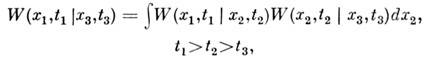
от к-рого можно перейти к кинетич. ур-нию

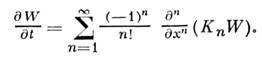
Здесь

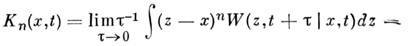
кинетич. коаф., описывающие локальные свойства M.с.п. в момент t в точке х. Для разрывных M.с.п., реализации к-рых скачком меняют значения в случайные моменты времени, кинетич. ур-ния эквивалентны интегро-дифференц. Колмогорова - Феллера уравнениям.

M.с.п., реализации к-рых с вероятностью 1 непрерывны во времени, наз. непрерывными или диффузионными процессами. Для них отличны от нуля только два кинетич. коэф.: коэф. сноса

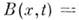
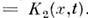и коэф. диффузии . При этом кинетич. ур-ние переходит в Фоккера - Планка уравнение (см. также Колмогорова уравнения):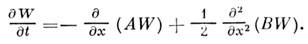

Ес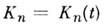ли или 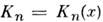, то M.с.п. наз. однородным в пространстве или во времени. В последнем случае плотность вероятности переходов зависит лишь от разности времён: 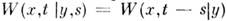Простейшим однородным в пространстве и во времени непрерывным M. с. п. является винеровский случайный процесс, для к-рого 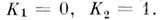Он описывает, напр., свободную диффузию частиц в среде с пост, темп-рой. Простейшим однородным во времени процессом является процесс Орнштейна- Уленбека, для к-рого 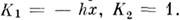Ур-ние Фоккера - Планка в этом случае имеет вид

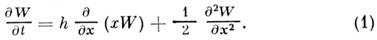
Статистич. характеристики M. с. п. находят, исследуя решения кинетич. ур-ний с теми или иными начальными и граничными условиями. Так, плотность вероятности переходов процесса Орнштейна - Уленбека, удовлетворяющая ур-нию (1) с начальным условием

)

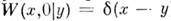равна

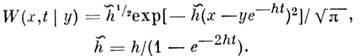
Для однородных во времени процессов может существовать стационарная плотность вероятности

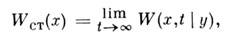
удовлетворяющая, в случае диффузионного процесса, обыкновенному дифференц. ур-нию

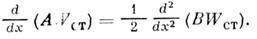
При анализе M. с. п., реализации к-рых обрываются или отражаются на заданных границах, кинетич. ур-ния дополняют граничными условиями.

Реализации M. с. п. с непрерывным временем удовлетворяют дифференц. стохастическим уравнениям. Напр., реализации диффузионного процесса X(t)удовлетворяют ур-нию

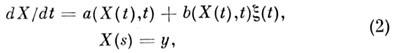
здесь 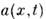и- 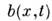детерминиров. ф-ции, а- 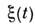белый шум, для к-рого

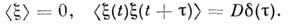
Кинетич. коэф. диффузионного процесса, описываемого ур-нием (2), равны: