Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Средняя арифметическая.
|
|
Средняя арифметическая простая рассчитывается как сумма значений, деленное на их количество и в математической форме имеет вид:
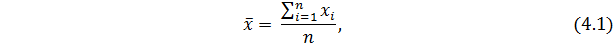
где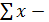 
сумма индивидуальных значений величины признака x;
n – количество индивидуальных значений.
Пример 1. Определить средний возраст работников цеха по следующим данным.
Возраст работников представлен в таблице 4.1.
Таблица 4.1
| Табельный номер работника | ||||||||||||
| Возраст (лет) |
Решение:
Средний возраст работников бригады составит:
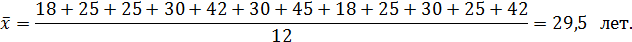
Если исходные данные сгруппировать и представить в виде ряда распределения, то используется средняя арифметическая взвешенная, которая имеет следующий вид:
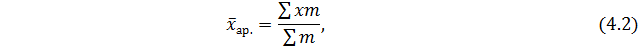
где x – индивидуальное значение признака;
m – количество единиц, имеющих данную величину признака
(частота повторения признака).
Пример 2. На основании данных примера 1 составим распределение работников по возрасту используя дискретную группировку (таблица 4.2) и рассчитаем средний возраст.
Таблица 4.2
| Возраст работников (лет) x | Количество работников, m | хm |
| Итого |
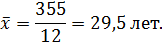
В следующем примере показывается использование средней арифметической взвешенной на примере интервального ряда.
Пример 3. Имеются данные о заработной плате работников цеха. Определить среднюю заработную плату.
Таблица 4.3
| Заработная плата, тыс. руб. | Количество работников, m | Середина интервала, x | xm |
| До 10 10-15 15-20 20-25 25-30 Свыше 30 | 7, 5 12, 5 17, 5 22, 5 27, 5 32, 5 | 262, 5 | |
| Итого | 897, 5 |
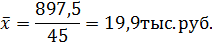
Средняя арифметическая обладает рядом свойств, которые используются для упрощения расчета средней. Одним из свойств средней арифметической является ее определение по способу моментов. Этот способ можно использовать, если ряд распределения, для которого рассчитывается средняя, составляет арифметическую прогрессию или имеющего равные интервалы.
Расчеты ведутся в следующей последовательности:
1. Находится варианта (А), которая соответствует наибольшей частоте.
2. Определяются новые варианты x для каждой группы по формуле:
где i – величина интервала.
3. Находится новая средняя по формуле:
4. Средняя величина фактического ряда определяется по формуле:
= 
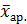(4.5)
Пример 4. Имеются данные о количестве посылок, обрабатываемых за год на почтамтах ФГУП. Определить среднее количество обрабатываемых посылок.
Таблица 4.4
| Количество обрабатываемых посылок, тыс. ед. | Количество почтамтов |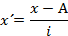 
| 
|
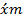
| До 120 120-130 130-140 140-150 150-160 Более 160 | -3 -2 -1 | -9 -8 -7 | |
| Итого | -14 |
Решение:
А=145
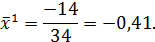
Среднее количество обрабатываемых посылок:
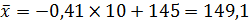тыс. ед.