
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вариационные ряды, их виды. Графическое изображение вариационных рядов
|
|
Вариацией называется различие значений признака у отдельных единиц изучаемой совокупности в один и тот же период или момент времени.
Статистический анализ вариации предполагает:
1. Построение вариационного ряда
2. Графическое изображение вариационного ряда
3. Расчет основных характеристик вариационного ряда.
Построение вариационного ряда (ряд распределения) – это упорядоченное распределение единиц совокупности по возрастающим или убывающим значениям признака.
В составе любого вариационного ряда можно выделить три основных элемента: варианта, частота и частость.
Варианта – это значения, которые принимает исследуемый признак и обозначается через x.
Частоты вариационного ряда – абсолютная численность отдельных групп с различными значениями признака, обозначается через m.
Частости вариационного ряда – удельные веса (доли) отдельных групп в общей совокупности.
Вариационные ряды бывают двух видов:
- дискретные;
- интервально-вариационные.
В дискретных рядах варианты представлены в виде целочисленных величин. Если варианты представлены в виде интервалов, то такие ряды называются интервально-вариационными.
Для анализа вариационных рядов и определения формы распределения используются графики. При графическом изображении вариационного ряда в статистике используется полигон распределения, гистограмма и кумулята.
Чтобы построить полигон распределения на оси абсцисс отмечают точки, соответствующие величине вариант значений признака из них восстанавливаются перпендикуляры, длине которых соответствует частота этих вариант по принятому масштабу на оси ординат. Вершины перпендикуляров соединяются отрезками прямой.
Графическое изображение дискретного ряда, приведенного в таблице 4.2, глава «Средние величины») представлено на рис. 5.1.
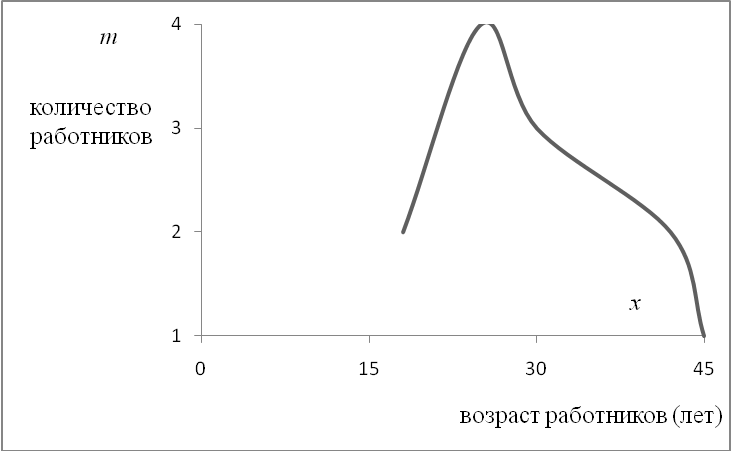
Рис. 5.1. Полигон распределения работников по возрасту
Для графического изображения интервального ряда используется гистограмма.
Гистограмма – столбиковая диаграмма, для построения которой на оси абсцисс откладываются отрезки, равные величине интервалов вариационного ряда. На отрезках строят прямоугольники, высота которых в принятом масштабе по оси ординат соответствует частотам или частостям. Графическое изображение интервально-вариационного ряда, приведенного в таблице 4.3 (глава 4, «Средние величины») представлено на рис. 5.2.
| х |
| 5 10 15 Mо 20 25 30 35 |
| Количество работников |
| m |
| Заработная плата, тыс. руб. |
Рис. 5.2. Гистограмма распределения работников по величине заработной платы
По гистограмме можно определить показатель центра распределения – моду (М0), который будет рассмотрен далее.
Кумулята – распределение строится по накопленным частотам, они определяются последовательным суммированием частот.
Накопленные частоты показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение.
Накопленные частоты по рассматриваемому предыдущему примеру (таб. 4.3) будут равны:
1 группа (до 10 тыс. руб.) – 2;
2 группа (от 10-15) – 10;
3 группа (от 15-20) – 25;
4 группа (от 20-25) – 35;
5 группа (от 25-30) – 41;
6 группа (свыше 30) – 45.
Кумулята распределения работников по заработной плате представлена на рис. 5.3.
| Ме |
| 0 7, 5 12, 5 17, 5 22, 5 27, 5 32, 5 |
| x |
| m |
Рис. 5.3. Кумулята распределения работников по заработной плате
По кумуляте можно определить еще один показатель центра распределения – медиану (Ме).