Показатели вариации. При изучении вариационных рядов рассчитываются показатели, характеризующие размер и интенсивность вариации.

При изучении вариационных рядов рассчитываются показатели, характеризующие размер и интенсивность вариации.

Для характеристики размера вариации рассчитываются абсолютные показатели вариации:

- размах вариации;

- среднее линейное отклонение;

- среднее квадратическое отклонение;

- дисперсия.

Размах вариации определяется по формуле:

где 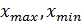- максимальное и минимальное значение признака в

совокупности.

Среднее линейное отклонение рассчитывается как:

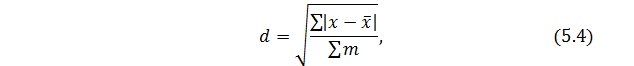
Для определения среднего квадратического отклонения используется формула:

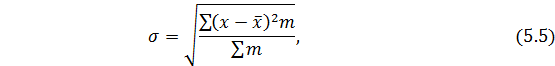
Данный показатель характеризует, насколько в среднем значения признака отклоняются от средней величины.

Дисперсия – это квадрат среднего квадратического отклонения:

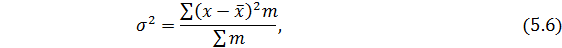
Все рассмотренные показатели, исключая дисперсию измеряются в тех же единицах, что и варианта. Дисперсия единицы измерения не имеет.

Для оценки интенсивности вариации используется относительный показатель – коэффициент вариации, рассчитываемый по формуле:

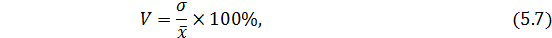
Он показывает, во-первых, на сколько процентов в среднем значения признака отклоняются от среднего, а во-вторых, характеризует степень однородности совокупности.

Если коэффициент вариации 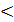33%, то означает, что совокупность однородная, а средняя типична для данной совокупности, и ее можно использовать в дальнейших расчетах. В случае, если коэффициент получается 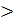33%, необходимо изучаемую совокупность разделить на группы и в каждой группе рассчитать свою среднюю.