
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 2. В результате обследования рабочих одной и той же профессии по уровню образования и степенью удовлетворенности работой получены следующие данные.
|
|
В результате обследования рабочих одной и той же профессии по уровню образования и степенью удовлетворенности работой получены следующие данные.
Таблица 9.5 Распределение рабочих по уровню образования и удовлетворенностью работой
| Группы работников по образованию | Численность работников, давших ответ на вопрос об удовлетворенности работой | |||||
| 1.Незаконченное среднее | ||||||
| 2.Среднее | ||||||
| 3.Среднее специальное | ||||||
| Итого: |
Данные таблицы показывают, что существует стохастическая связь между признаками, то есть каждому значению факторного признака соответствует несколько значений результативного. В то время как среди рабочих со средним специальным образованием большинство не удовлетворено работой, то среди рабочих с незаконченным средним образованием неудовлетворенные работой составляют меньшинство.
Более наглядно связь между признаками возможно показать, определив частности условных распределений рабочих для каждого уровня образования, это представлено в таблице.
Таблица 9.6 Расчетная таблица
| Группы работников по образованию | Численность работников, давших ответ на вопрос об удовлетворенности работой | |||||
| Неудовлетворенность | Скорее неудовлетворенность, чем удовлетворенность | Отношусь безразлично | Скорее удовлетворенность, чем неудовлетворенность | Удовлетворенность | Итого | |
| 1.Незаконченное среднее | 0, 035 | 0, 053 | 0, 105 | 0, 386 | 0, 421 | 1, 000 |
| 2.Среднее | 0, 234 | 0, 102 | 0, 181 | 0, 354 | 0, 228 | 1, 000 |
| 3.Среднее специальное | 0, 302 | 0, 431 | 0, 086 | 0, 103 | 0, 078 | 1, 000 |
| Итого: | 0, 180 | 0, 220 | 0, 130 | 0, 263 | 0, 207 | 1, 000 |
Стохастическая зависимость проявляется в различиях условных распределений. При отсутствии стохастической зависимости частности условных распределений совпадают и равны частностям распределения по итоговой строке (безусловного распределения). Чем больше частности условных распределений отличаются от частности безусловного распределения, тем в большей мере признаки связаны между собой.
Теснота стохастической связи измеряется коэффициентом взаимной сопряженности, расчет которого основан на разностях частностей условного и безусловного распределения. Для каждого условного распределения вычисляется величина x 2 по формуле:

где 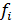 - количество человек в каждой i- й группе рабочих по уровню
- количество человек в каждой i- й группе рабочих по уровню
образования;
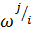 - частность j- го столбца условного распределения по i -й строке;
- частность j- го столбца условного распределения по i -й строке;
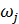 - частность того же столбца в безусловном распределении;
- частность того же столбца в безусловном распределении;
m – количество групп по результативному признаку.
На основании 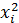 определяется значение x2 для всей совокупности.
определяется значение x2 для всей совокупности.
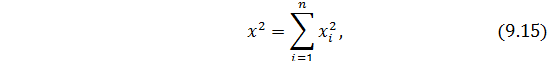
где n – количество групп работников по образованию.
На основании данных таблицы по формуле можно определить:
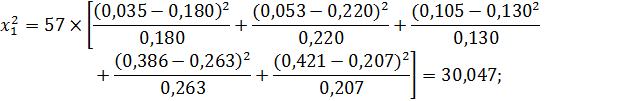
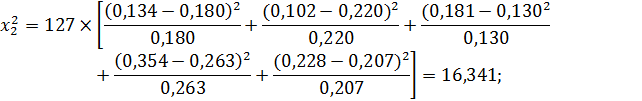

На основании рассчитанных данных 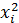 можно определить:
можно определить:
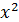 =30, 047+16, 341+55, 411=101, 799.
=30, 047+16, 341+55, 411=101, 799.
При неравном числе групп (mi≠ m2) коэффициент взаимной сопряженности определяется по формуле Крамера:
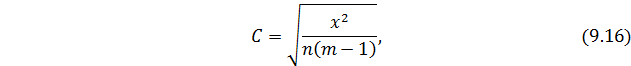
где m – минимальное значение из m1 и m2;
n – общее число работников.
Таким образом, С будет равно:
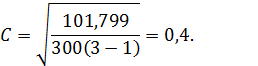
Значение коэффициента взаимной сопряженности по шкале Чеддока указывает на умеренную связь между удовлетворенностью работой и уровнем образования.
Проверка существенности стохастической связи производится с помощью критерия x2.
Число степеней свободы равно 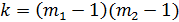 . В данном случае при уровне зависимости 0, 05 и
. В данном случае при уровне зависимости 0, 05 и 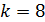 значения табличного значения критерия
значения табличного значения критерия 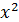 составляет 15, 51, что меньше фактического и доказывает наличие стохастической связи.
составляет 15, 51, что меньше фактического и доказывает наличие стохастической связи.
Метод изучения связи, основанный на определении коэффициента взаимной сопряженности по формуле Крамера, довольно прост, но не показывает направление связи между признаками. Более точно оценить взаимосвязь между признаками, не выраженными количественно, возможно с помощью методов ранговой корреляции.
Одним из методов ранговой корреляции является метод, основанный на расчете коэффициента корреляции рангов Кендэлла. При его определении сравниваются ранги для всех пар единиц совокупности, которые предварительно упорядочиваются по значениям факторного признака. Затем для каждой единицы совокупности подчитывается число балов. Для этого ранг по результативному признаку данной единицы совокупности сравниваемых с рангами всех других единиц, расположенных ниже данной и имеющих другие падающие ранги по факторному признаку. Если ранг по результативному признаку больше ранга другой единицы, то отличается +1, а в противном случае отличается -1, при совпадающих рангах баллы не подчитываются. Поскольку при расчете коэффициента Кендэлла не используются сами значения рангов, а только устанавливаются больше или меньше ранг данной единицы, то нет необходимости при совпадении значений признаков вычислять средний ранг.
Коэффициент Кендэлла может быть вычислен также по таблицам взаимной сопряженности, если группы по каждому признаку упорядочены. Расчеты можно провести по данным таблицы.
Группе работников с незаконченным средним образованием присвоен ранг 1, со средним – ранг 2, со средним специальным – 3. Ответ на вопрос об удовлетворенности работой пронумерованы от 1 (не удовлетворен) до 5 (удовлетворен).
Все единицы, принадлежащие к одной группе, имеют одинаковые ранги. Поэтому подчитывается число баллов у одной единицы, которое затем умножается на частоту этой подгруппы. Сравнение производится только для строк ниже данной. Сумма частот в клетках справа от данного столбца дает сумму положительных баллов (ранги по второму признаку выше, чем в данной подгруппе). Сумма частот в клетках слева от данного столба дает сумму отрицательных баллов.
Коэффициент Кендэлла определяется по формуле:
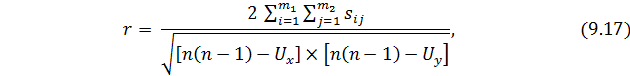
где 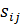 – сумма баллов у единиц подгруппы на пересечении i -й строки и
– сумма баллов у единиц подгруппы на пересечении i -й строки и
j -го столбца;
 - количество рабочих;
- количество рабочих;

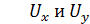 - поправки, связанные с совпадением рангов соответственно
- поправки, связанные с совпадением рангов соответственно
по факторному и результативному признаку, и
определяются по формуле:
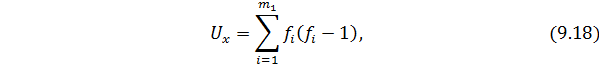
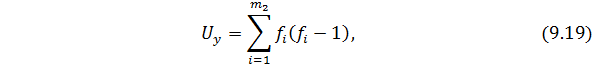
где 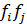 - частоты безусловных распределений по факторному и
- частоты безусловных распределений по факторному и
результативному признаку.
Рассчитанные суммы баллов для каждой подгруппы 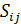 представлены в таблице 9.7.
представлены в таблице 9.7.
Таблица 9.7 Расчеты величин для определения коэффициента Кендэлла
| Ранг факторного признака | Ранг результативного признака | |||||
| Итого | ||||||
| -120 | -2420 | -4920 | -6850 | |||
| -52 | -1472 | -3870 | -3103 | -7120 | ||
| Итого | -1592 | -6290 | -8023 | -13970 |
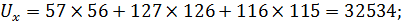
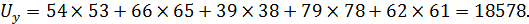
По формуле 9.22 определяется значение коэффициента Кендэлла:
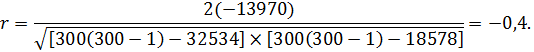
Значение коэффициента Кендэлла говорит об умеренной обратной связи между уровнем образования и удовлетворенностью работой.
Абсолютное значение коэффициента Кендэлла равно коэффициенту взаимной сопряженности Крамера. Это говорит о том, что оба метода дают одинаковый результат, но коэффициент Кендэлла кроме абсолютного значения связи показывает и ее направление. Следовательно, для более глубокого анализа рекомендуется использовать коэффициент Кендэлла и ранговый корреляции.
Вопросы для самопроверки
1. Какие существуют виды корреляционной связи?
2. Чем отличается функциональная связь от корреляционной?
3. Назовите этапы выполнения корреляционного анализа
4. Какие существуют формы связи?
5. Что показывает коэффициент корреляции?
6. Для чего строится поле корреляции?
7. Что определяется с помощью уравнения регрессии?
Тест для самопроверки к теме 9 «Статистические методы изучения взаимосвязи социально-экономических явлений»
1. Что невозможно выявить по полю корреляции:
1. тесноту взаимосвязи
2. форму связи
3. наличие связи
4. направление связи
2. Коэффициент корреляции равен R=-0, 25. Это означает:
1. связь слабая
2. связь сильная
3. такого не бывает
4. связь заметная
3. Что означает «коленеарность» в корреляционном анализе:
1. тесноту взаимосвязи между x и y
2. количественную оценку в нелинейной зависимости
3. тесноту взаимосвязи между факторными признаками в многофакторных зависимостях
4. обратную зависимость