Связь устойчивости с корнями характеристического уравнения

Существуют следующие способы определения устойчивости:

1) прямой – путем решения дифференциального уравнения и анализа этого уравнения;

2) по корням характеристического уравнения;

3) по критериям устойчивости.

Рассмотрим способ 2.

Пусть динамика САУ описывается уравнением:

Приложим к системе внешнее воздействие, а затем снимем его. Это будет соответствовать нулевой правой части.

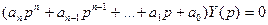
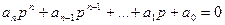- характеристическое уравнение системы.

Корни характеристического уравнения определяют вид переходной составляющей в решении дифференциального уравнения. Проанализируем поведение системы для различных корней:

1) вещественный корень 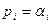- в решении ему будет соответствовать вида :

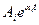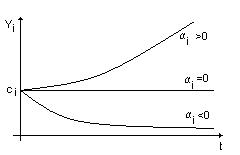
а) 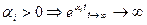-экспонента будет неограниченно возрастать, переходный процесс расходится, система неустойчива.

б) 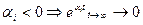- имеем сходящийся переходный процесс, система устойчива.

в) 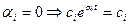- имеем нейтрально устойчивую систему, переходного процесса нет.

2) Пара комплексно-сопряженных корней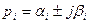

В решении имеем составляющую вида: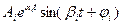

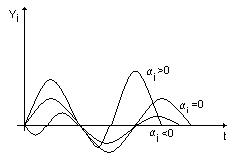
а) 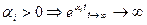- имеем расходящийся переходный процесс, система неустойчива.

б) 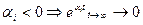- имеем сходящийся переходный процесс, система устойчива.

в) 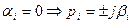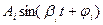- имеем незатухающие колебания, система находится на грани устойчивости.

г) 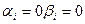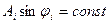- переходного процесса нет, имеем нейтрально устойчивую систему.

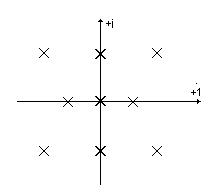
Вывод: для устойчивости САУ необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательную вещественную часть.

Реальные системы нелинейны и мы проводим их линеаризацию. Чтобы распространить сделанные выводы о корнях на линеаризованные системы, А.А. Ляпунов доказал следующие теоремы:

I теорема: Если линеаризованная система устойчива, то никакие из отброшенных при линеаризации корней не могут сделать ее неустойчивой.

II теорема: Если линеаризованная система неустойчива, то никакие из отброшенных при линеаризации корней не могут сделать ее устойчивой.

III теорема: Если линеаризованная система находится на грани устойчивости, то устойчивость реальной системы определяется корнями, отброшенными при линеаризации.