
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейная модель.
|
|
Построим линейную модель, включающую все переменные.
Модель 1: МНК, использованы наблюдения 1-153
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-статистика | P-значение | ||
| const | -5, 02835e+06 | 1, 07755e+06 | -4, 6665 | < 0, 00001 | *** |
| length | 44683, 9 | 3, 8972 | 0, 00015 | *** | |
| beam | 1, 7813 | 0, 07703 | * | ||
| draft | 2, 3343 | 0, 02100 | ** | ||
| displacement | -11498, 6 | -1, 5130 | 0, 13254 | ||
| max_speed | -1322, 43 | 48204, 4 | -0, 0274 | 0, 97815 | |
| cruising_speed | 36094, 7 | 53087, 2 | 0, 6799 | 0, 49768 | |
| power | -184, 244 | 117, 736 | -1, 5649 | 0, 11986 | |
| fuel | 216, 728 | 46, 9857 | 4, 6126 | < 0, 00001 | *** |
| water | -246, 793 | 184, 203 | -1, 3398 | 0, 18249 | |
| cabin | -168766 | -0, 7287 | 0, 46738 | ||
| guest | 13858, 2 | 0, 1225 | 0, 90268 | ||
| region | -195736 | -1, 1731 | 0, 24276 |
| Среднее зав. перемен | Ст. откл. зав. перемен | |||
| Сумма кв. остатков | 1, 05e+14 | Ст. ошибка модели | 866624, 0 | |
| R-квадрат | 0, 768623 | Испр. R-квадрат | 0, 748790 | |
| F(12, 140) | 38, 75599 | Р-значение (F) | 1, 50e-38 | |
| Лог. правдоподобие | -2302, 176 | Крит. Акаике | 4630, 352 | |
| Крит. Шварца | 4669, 747 | Крит. Хеннана-Куинна | 4646, 355 |
В этой модели переменные length, const и fuel значимы на 1% уровне, draft на 5 % уровне и beam на 10% уровне. Все остальные переменные оказались незначимыми. В целом уравнение значимо на 1% уровне и R2 = 0.76823.
Данные результаты (небольшое количество значимых переменных при значимом уравнении в целом) свидетельствуют о наличии мультиколлинеарности в модели. Проведенный тест на мультиколлинеарность подтверждает мои предположения. Таким образом, сделанные мной выводы о необходимом исключении переменных (guest, cruising_speed) оказались правильными.
Построим линейную модель без переменных guest и cruising_speed.
Модель 2: МНК, использованы наблюдения 1-153
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-статистика | P-значение | ||
| const | -5, 14094e+06 | 1, 05869e+06 | -4, 8560 | < 0, 00001 | *** |
| length | 44021, 4 | 3, 9240 | 0, 00014 | *** | |
| beam | 1, 9000 | 0, 05946 | * | ||
| draft | 2, 4176 | 0, 01689 | ** | ||
| displacement | -12380, 4 | 7438, 33 | -1, 6644 | 0, 09824 | * |
| max_speed | 29808, 7 | 15009, 5 | 1, 9860 | 0, 04896 | ** |
| power | -180, 854 | 116, 982 | -1, 5460 | 0, 12433 | |
| fuel | 222, 842 | 45, 8429 | 4, 8610 | < 0, 00001 | *** |
| water | -261, 857 | 178, 225 | -1, 4692 | 0, 14398 | |
| cabin | -147276 | 89416, 9 | -1, 6471 | 0, 10175 | |
| region | -175152 | -1, 0741 | 0, 28461 |
| Среднее зав. перемен | Ст. откл. зав. перемен | |||
| Сумма кв. остатков | 1, 05e+14 | Ст. ошибка модели | 861919, 9 | |
| R-квадрат | 0, 767858 | Испр. R-квадрат | 0, 751510 | |
| F(10, 142) | 46, 96944 | Р-значение (F) | 4, 00e-40 | |
| Лог. правдоподобие | -2302, 428 | Крит. Акаике | 4626, 857 | |
| Крит. Шварца | 4660, 191 | Крит. Хеннана-Куинна | 4640, 398 |
В данной модели length, fuel, const значимы на 1% уровне, draft, max_speed на 5% уровне, beam, displacement на 10% уровне. Уравнение в целом также значимо на 1% и R2= 0, 767858.
Так как следующим шагом будет исключение незначимых переменных из модели, а фиктивная переменная не является значимой, то проинтерпретируем коэффициент при фиктивной переменной region.
Коэффициент при переменной region означает, что цена яхты в Америке на 175152 евро выше, чем цена яхты в Европе.
Таким образом, количество значимых переменных в модели увеличилось, но все равно не все переменные стали значимыми.
Мною принято решение убрать незначимые переменные, при этом оставив такие переменные как power и cabin, так как, на мой взгляд, мощность является неотъемлемой характеристикой любого транспортного средства, а количество кают отображает возможное число гостей хозяина яхты. Построим данную модель.
Модель 3: МНК, использованы наблюдения 1-153
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-статистика | P-значение | ||
| const | -5, 40916e+06 | 1, 05111e+06 | -5, 1461 | < 0, 00001 | *** |
| length | 43971, 7 | 3, 7491 | 0, 00026 | *** | |
| beam | 2, 0736 | 0, 03990 | ** | ||
| draft | 2, 5966 | 0, 01039 | ** | ||
| displacement | -14319 | 7300, 86 | -1, 9613 | 0, 05178 | * |
| max_speed | 14436, 6 | 2, 1272 | 0, 03511 | ** | |
| power | -202, 767 | 116, 92 | -1, 7342 | 0, 08502 | * |
| fuel | 198, 118 | 39, 7408 | 4, 9853 | < 0, 00001 | *** |
| cabin | -171202 | -1, 9281 | 0, 05581 | * |
| Среднее зав. перемен | Ст. откл. зав. перемен | |||
| Сумма кв. остатков | 1, 08e+14 | Ст. ошибка модели | 866147, 8 | |
| R-квадрат | 0, 762273 | Испр. R-квадрат | 0, 749066 | |
| F(8, 144) | 57, 71717 | Р-значение (F) | 3, 62e-41 | |
| Лог. правдоподобие | -2304, 247 | Крит. Акаике | 4626, 494 | |
| Крит. Шварца | 4653, 768 | Крит. Хеннана-Куинна | 4637, 573 |
В данной модели length, fuel, const значимы на 1% уровне, draft, beam, max_speed на 5% уровне. Переменные displacement, power и cabin незначимы на 5% уровне значимости, но значимы на 10% уровне. Уравнение в целом значимо на 1% уровне и R2 =0, 762273.
Для построения данной модели мы пользовались методом наименьших квадратов, но для данного метода одним из необходимых условий является отсутствие гетероскедастичности. Если в модели есть гетероскедастичность, то МНК-оценки коэффициентов становятся неэффективными и стандартные ошибки коэффициентов смещены и несостоятельны => t-статистики вычисляются некорректно.
Для обнаружения гетероскедастичности проведем тест Уайта.
Н0: в модели нет гетероскедастичности.
Тест Вайта (White) на гетероскедастичность
МНК, использованы наблюдения 1-153
Зависимая переменная: uhat^2
Коэффициент Ст. ошибка t-статистика P-значение
-----------------------------------------------------------------------------
const 2, 40754e+013 2, 14208e+013 1, 124 0, 2635
length 2, 19300e+011 9, 64988e+011 0, 2273 0, 8207
beam -8, 44924e+012 8, 12380e+012 -1, 040 0, 3006
draft -7, 86633e+012 5, 33894e+012 -1, 473 0, 1436
displacement 2, 48166e+011 2, 38617e+011 1, 040 0, 3007
max_speed -5, 59625e+011 4, 64055e+011 -1, 206 0, 2305
power 1, 06114e+010 5, 11135e+09 2, 076 0, 0403 **
fuel -4, 02562e+09 1, 29093e+09 -3, 118 0, 0023 ***
cabin 4, 13366e+012 2, 80202e+012 1, 475 0, 1431
sq_length -7, 85703e+010 3, 60375e+010 -2, 180 0, 0314 **
X2_X3 4, 25956e+011 2, 46097e+011 1, 731 0, 0863 *
X2_X4 2, 89243e+011 3, 06779e+011 0, 9428 0, 3479
X2_X5 2, 67882e+010 1, 06476e+010 2, 516 0, 0133 **
X2_X6 -3, 81329e+010 1, 63833e+010 -2, 328 0, 0218 **
X2_X7 1, 68880e+08 1, 64651e+08 1, 026 0, 3073
X2_X8 -1, 19766e+08 4, 49588e+07 -2, 664 0, 0089 ***
X2_X9 1, 62140e+011 1, 00063e+011 1, 620 0, 1081
sq_beam 3, 03925e+011 6, 18554e+011 0, 4913 0, 6242
X3_X4 8, 92396e+011 1, 57036e+012 0, 5683 0, 5710
X3_X5 -1, 27627e+011 6, 14778e+010 -2, 076 0, 0403 **
X3_X6 1, 69024e+011 1, 08645e+011 1, 556 0, 1227
X3_X7 -1, 87251e+09 1, 22996e+09 -1, 522 0, 1308
X3_X8 9, 83635e+08 3, 04710e+08 3, 228 0, 0017 ***
X3_X9 -1, 84479e+012 7, 32947e+011 -2, 517 0, 0133 **
sq_draft 5, 63266e+011 7, 46269e+011 0, 7548 0, 4520
X4_X5 -1, 28199e+011 4, 13969e+010 -3, 097 0, 0025 ***
X4_X6 -2, 36777e+09 5, 88167e+010 -0, 04026 0, 9680
X4_X7 5, 82182e+08 5, 56418e+08 1, 046 0, 2978
X4_X8 4, 51766e+08 2, 48950e+08 1, 815 0, 0723 *
X4_X9 -5, 88676e+011 5, 57806e+011 -1, 055 0, 2936
sq_displaceme 1, 10700e+09 6, 05385e+08 1, 829 0, 0702 *
X5_X6 5, 64435e+09 3, 19677e+09 1, 766 0, 0803 *
X5_X7 -7, 58590e+07 2, 18796e+07 -3, 467 0, 0008 ***
X5_X8 -1, 11236e+07 7, 09398e+06 -1, 568 0, 1198
X5_X9 -3, 57120e+09 1, 48899e+010 -0, 2398 0, 8109
sq_max_speed 4, 86841e+09 5, 21236e+09 0, 9340 0, 3524
X6_X7 -1, 95624e+08 6, 67602e+07 -2, 930 0, 0041 ***
X6_X8 1, 57180e+07 2, 24268e+07 0, 7009 0, 4849
X6_X9 2, 21308e+010 3, 32422e+010 0, 6657 0, 5070
sq_power 1, 34639e+06 358375 3, 757 0, 0003 ***
X7_X8 -76908, 9 112223 -0, 6853 0, 4946
X7_X9 1, 20886e+08 2, 66676e+08 0, 4533 0, 6512
sq_fuel 17609, 3 27382, 6 0, 6431 0, 5215
X8_X9 1, 49490e+08 8, 21010e+07 1, 821 0, 0714 *
sq_cabin 3, 29007e+011 1, 45331e+011 2, 264 0, 0256 **
ВНИМАНИЕ: матрица данных близка к сингулярной!
Неисправленный R-квадрат = 0, 705925
Тестовая статистика: TR^2 = 108, 006569,
р-значение = P(Хи-квадрат(44) > 108, 006569) = 0, 000000
Так как тестовая статистика больше p-значения, то Н0 отвергается, то есть в модели есть гетероскедастичность.
Проведем коррекцию ошибок в формуле Уайта.
Предположим, что для суммы квадратов остатков верна следующая зависимость:

Оцениваем параметры модели. Получаем ряд 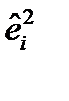 .
.
Используем оценку дисперсии: 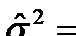 .
.
В качестве весов возьмем переменную w1=1/ 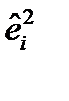 .
.
Модель 4: ВМНК, использованы наблюдения 1-153
Зависимая переменная: price
Весовая переменная: w1
| Коэффициент | Ст. ошибка | t-статистика | P-значение | ||
| const | -5, 27394e+06 | 1, 03276e+06 | -5, 1066 | < 0, 00001 | *** |
| length | 43299, 1 | 3, 7161 | 0, 00029 | *** | |
| beam | 2, 0518 | 0, 04200 | ** | ||
| draft | 2, 4677 | 0, 01477 | ** | ||
| max_speed | 30938, 4 | 14201, 7 | 2, 1785 | 0, 03100 | ** |
| fuel | 199, 891 | 39, 5985 | 5, 0480 | < 0, 00001 | *** |
| cabin | -163860 | 87783, 3 | -1, 8666 | 0, 06399 | * |
| power | -201, 515 | 117, 014 | -1, 7222 | 0, 08719 | * |
| displacement | -13377, 3 | 7277, 62 | -1, 8381 | 0, 06810 | * |
Статистика, полученная по взвешенным данным:
| Сумма кв. остатков | 4, 10e+12 | Ст. ошибка модели | 168696, 4 | |
| R-квадрат | 0, 763332 | Испр. R-квадрат | 0, 750184 | |
| F(8, 144) | 58, 05607 | Р-значение (F) | 2, 64e-41 | |
| Лог. правдоподобие | -2053, 946 | Крит. Акаике | 4125, 892 | |
| Крит. Шварца | 4153, 166 | Крит. Хеннана-Куинна | 4136, 971 |
Статистика, полученная по исходным данным:
| Среднее зав. перемен | Ст. откл. зав. перемен | |||
| Сумма кв. остатков | 1, 08e+14 | Ст. ошибка модели | 866310, 2 |
В итоговой линейной модели отсутствует гетероскедастичность, все коэффициенты значимы на 10%, причем коэффициенты при const, length и fuel значимы на 1%, а при beam, draft, max_speed на 5%. В целом данное уравнении множественной регрессии значимо на 1% уровне. R2 = 0.763332 и R2 adj = 0.750184.
Полученная модель отображает линейную зависимость цены яхты от длины, ширины, осадки, водоизмещения судна, максимальной скорости, запаса топлива, числа кабин, а также мощности. В процессе улучшения модели фиктивная переменная region была исключена из модели, но была проинтерпретирована ранее.
Зависимость цены от ее характеристик выглядит следующим образом:
Price = -5, 27394e+06 +160906*length + 517151 * beam + 505904*draft + 30938, 4*max_speed + 199, 891* fuel - 163860 * cabin + -201, 515 * power -13377, 3 displacement
Проинтерпретируем коэффициенты при переменных в данной модели:
ü При увеличении длины судна на 1 метр, цена яхты увеличится на 160906 евро;
ü При увеличении ширины судна на 1 метр, цена яхты увеличится на 517151 евро;
ü При увеличении осадки судна на 1 метр, цена яхты увеличится на 539224 евро;
ü При увеличении водоизмещения яхты на 1 тонну, цена яхты уменьшится на 13377, 3 евро;
ü При увеличении максимальной скорости на 1 узел, цена яхты увеличится на 30938, 4 евро;
ü При увеличении запаса топлива на 1 литр, цена яхты увеличится практически на 200 евро;
ü При увеличении количества кают на 1, цена яхты уменьшится на 163860 евро;
ü При увеличении мощности на 1 HP, цена яхты уменьшится на 201 евро.
Среди недостатков данной скорректированной модели следует выделить отсутствие наилучших оценок среди линейных несмещенных оценок.