
Главная страница Случайная страница
КАТЕГОРИИ:
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Линейно – логарифмическая модель
|
|
Построим линейно-логарифмическую модель без переменных guest и cruising_speed, так как они способствовали появлению мультиколлинеарности в модели, и это было обосновано в линейной модели.
Модель 8: МНК, использованы наблюдения 1-153
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-статистика | P-значение | ||
| const | -1, 8149e+07 | 2, 01345e+06 | -9, 0139 | < 0, 00001 | *** |
| l_length | 3, 28178e+06 | 1, 07692e+06 | 3, 0474 | 0, 00275 | *** |
| l_beam | 3, 1294e+06 | 1, 72959e+06 | 1, 8093 | 0, 07251 | * |
| l_draft | 1, 3601 | 0, 17596 | |||
| l_displacemen | -478989 | -1, 1792 | 0, 24030 | ||
| l_max_speed | 1, 2159 | 0, 22605 | |||
| l_power | -334317 | -1, 2915 | 0, 19862 | ||
| l_fuel | 1, 35001e+06 | 3, 3940 | 0, 00089 | *** | |
| l_water | -514265 | -1, 6308 | 0, 10514 | ||
| l_cabin | -276725 | -0, 8279 | 0, 40912 | ||
| region | -116495 | -0, 6256 | 0, 53255 |
| Среднее зав. перемен | Ст. откл. зав. перемен | |||
| Сумма кв. остатков | 1, 34e+14 | Ст. ошибка модели | 972806, 8 | |
| R-квадрат | 0, 704285 | Испр. R-квадрат | 0, 683460 | |
| F(10, 142) | 33, 81923 | Р-значение (F) | 8, 28e-33 | |
| Лог. правдоподобие | -2320, 945 | Крит. Акаике | 4663, 890 | |
| Крит. Шварца | 4697, 224 | Крит. Хеннана-Куинна | 4677, 431 |
В данной модели коэффициенты при const, l_length, l_fuel значимые на 1% уровне, l_beam на 10 % уровне. Уравнение в целом значимое на 1 % уровне значимости и R2= 0, 704285.
Полученные результаты свидетельствуют о наличии мультиколлинерности в модели. (мало значимых переменных, а уравнение в целом значимо). В результате проведенного теста на мультиколлениарность было обнаружено, что переменная l_fuel является причиной данной проблемы. Исключим данную переменную.
Модель 9: МНК, использованы наблюдения 1-153
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-статистика | P-значение | ||
| const | -1, 6953e+07 | 2, 05399e+06 | -8, 2537 | < 0, 00001 | *** |
| l_length | 3, 62544e+06 | 1, 11088e+06 | 3, 2636 | 0, 00138 | *** |
| l_beam | 4, 73904e+06 | 1, 72339e+06 | 2, 7498 | 0, 00673 | *** |
| l_draft | 1, 7703 | 0, 07881 | * | ||
| l_displacemen | -54419, 6 | -0, 1359 | 0, 89209 | ||
| l_max_speed | 1, 0411 | 0, 29958 | |||
| l_power | -213207 | -0, 8026 | 0, 42354 | ||
| l_water | 93090, 9 | 0, 3460 | 0, 72983 | ||
| l_cabin | -309391 | -0, 8937 | 0, 37298 | ||
| region | -267874 | -1, 4301 | 0, 15487 |
| Среднее зав. перемен | Ст. откл. зав. перемен | |||
| Сумма кв. остатков | 1, 45e+14 | Ст. ошибка модели | ||
| R-квадрат | 0, 680296 | Испр. R-квадрат | 0, 660175 | |
| F(9, 143) | 33, 80991 | Р-значение (F) | 3, 06e-31 | |
| Лог. правдоподобие | -2326, 912 | Крит. Акаике | 4673, 823 | |
| Крит. Шварца | 4704, 128 | Крит. Хеннана-Куинна | 4686, 134 |
В данной модели коэффициенты при const, l_length, l_beam значимы на 1%, а при l_draft на 10 % уровне.
Было решено исключить незначимые переменные кроме l_max_speed, l_power и l_cabin, так как на мой взгляд, данные параметры очень важны при формировании цены яхт.
Проинтерпретируем коэффициент при фиктивной переменной region (1- Европа, 0-Америка):
Цена яхты в Европе на 309391 евро ниже, чем цена яхты в Америке.
Модель 10: МНК, использованы наблюдения 1-153
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-статистика | P-значение | ||
| const | -1, 61656e+07 | 1, 58912e+06 | -10, 1727 | < 0, 00001 | *** |
| l_length | 3, 51482e+06 | 3, 5635 | 0, 00049 | *** | |
| l_beam | 5, 06154e+06 | 1, 60009e+06 | 3, 1633 | 0, 00190 | *** |
| l_draft | 1, 7327 | 0, 08527 | * | ||
| l_max_speed | 0, 8776 | 0, 38159 | |||
| l_power | -252497 | -0, 9890 | 0, 32429 | ||
| l_cabin | -361928 | -1, 0677 | 0, 28743 |
| Среднее зав. перемен | Ст. откл. зав. перемен | |||
| Сумма кв. остатков | 1, 48e+14 | Ст. ошибка модели | ||
| R-квадрат | 0, 674912 | Испр. R-квадрат | 0, 661552 | |
| F(6, 146) | 50, 51811 | Р-значение (F) | 3, 04e-33 | |
| Лог. правдоподобие | -2328, 189 | Крит. Акаике | 4670, 379 | |
| Крит. Шварца | 4691, 592 | Крит. Хеннана-Куинна | 4678, 996 |
В данной модели коэффициенты при const, l_lenght, l_beam, значимы на 1% уровне значимости, при l_draft на 10% уровне. Уравнение в целом значимо на 1% и R2= 0, 674912.
Коэффициенты при l_max_speed, l_cabin и l_power не являются значимыми. С помощью теста на линейное ограничение проверим равенство коэффициентов при данных переменных нулю.
H0: b[l_max_speed] = 0
F(1, 146) = 0, 770214, р-значение = 0, 381593
Так как р-значение меньше тестовой статистики, то Н0 принимается, и это означает, что коэффициент при данной переменной равен нулю.
Н0: b[l_power] =0
F(1, 146) = 0, 97815, р-значение = 0, 324292
Так как р-значение меньше тестовой статистики, то Н0 принимается, и это означает, что коэффициент при данной переменной равен нулю.
H0: b[l_cabin]=0
F(1, 146) = 1, 13994, р-значение = 0, 287427
Так как р-значение меньше тестовой статистики, то Н0 принимается, и это означает, что коэффициент при данной переменной равен нулю.
Таким образом, нужно исключить данные переменные из модели.
Модель 11: МНК, использованы наблюдения 1-153
Зависимая переменная: price
| Коэффициент | Ст. ошибка | t-статистика | P-значение | ||
| const | -1, 5307e+07 | 1, 14931e+06 | -13, 3184 | < 0, 00001 | *** |
| l_length | 3, 2356e+06 | 3, 4102 | 0, 00084 | *** | |
| l_beam | 4, 47475e+06 | 1, 5185e+06 | 2, 9468 | 0, 00373 | *** |
| l_draft | 1, 4519 | 0, 14863 |
| Среднее зав. перемен | Ст. откл. зав. перемен | |||
| Сумма кв. остатков | 1, 51e+14 | Ст. ошибка модели | ||
| R-квадрат | 0, 668538 | Испр. R-квадрат | 0, 661864 | |
| F(3, 149) | 100, 1746 | Р-значение (F) | 1, 50e-35 | |
| Лог. правдоподобие | -2329, 675 | Крит. Акаике | 4667, 350 | |
| Крит. Шварца | 4679, 471 | Крит. Хеннана-Куинна | 4672, 274 |
В данной модели коэффициенты при const, l_length, l_beam на 1% уровне. Уравнение в целом является значимым на 1% уровне и R2 = 0, 668538.
Проведем тест Уайта на гетероскедастичность, так как метод МНК можно применять лишь при отсутствии гетероскедастичности.
Н0: в модели нет гетероскедастичности
Тест Вайта (White) на гетероскедастичность
МНК, использованы наблюдения 1-153
Зависимая переменная: uhat^2
Коэффициент Ст. ошибка t-статистика P-значение
------------------------------------------------------------------
const 6, 00346e+013 2, 91142e+013 2, 062 0, 0410 **
l_length 4, 51192e+012 3, 33044e+013 0, 1355 0, 8924
l_beam -7, 96889e+013 5, 58662e+013 -1, 426 0, 1559
l_draft -2, 42108e+013 8, 39166e+012 -2, 885 0, 0045 ***
sq_l_length -3, 02120e+011 1, 29880e+013 -0, 02326 0, 9815
X2_X3 -1, 96861e+012 3, 27349e+013 -0, 06014 0, 9521
X2_X4 8, 78593e+012 8, 69348e+012 1, 011 0, 3139
sq_l_beam 2, 58137e+013 2, 54149e+013 1, 016 0, 3115
X3_X4 -8, 85192e+011 1, 37071e+013 -0, 06458 0, 9486
sq_l_draft 9, 41496e+011 1, 89302e+012 0, 4974 0, 6197
Неисправленный R-квадрат = 0, 286356
Тестовая статистика: TR^2 = 43, 812479,
р-значение = P(Хи-квадрат(9) > 43, 812479) = 0, 000002
Таким образом, в модели есть гетероскедастичность.
Проведем коррекцию ошибок в формуле Уайта.
Предположим, что зависимость квадратных остатков описывается следующим образом:

Оцениваем параметры модели. Получаем ряд 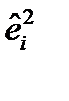 .
.
Используем оценку дисперсии: 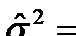 .
.
В качестве весов возьмем переменную w3=1/ 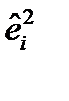 .
.
Модель 12: ВМНК, использованы наблюдения 1-153
Зависимая переменная: price
Весовая переменная: w3
| Коэффициент | Ст. ошибка | t-статистика | P-значение | ||
| const | -1, 51531e+07 | 1, 13625e+06 | -13, 3361 | < 0, 00001 | *** |
| l_length | 3, 18289e+06 | 3, 4072 | 0, 00084 | *** | |
| l_beam | 4, 483e+06 | 1, 4938e+06 | 3, 0011 | 0, 00316 | *** |
| l_draft | 1, 3856 | 0, 16793 |
Статистика, полученная по взвешенным данным:
| Сумма кв. остатков | 5, 66e+12 | Ст. ошибка модели | 194913, 3 | |
| R-квадрат | 0, 668510 | Испр. R-квадрат | 0, 661836 | |
| F(3, 149) | 100, 1621 | Р-значение (F) | 1, 51e-35 | |
| Лог. правдоподобие | -2078, 658 | Крит. Акаике | 4165, 317 | |
| Крит. Шварца | 4177, 439 | Крит. Хеннана-Куинна | 4170, 241 |
Статистика, полученная по исходным данным:
| Среднее зав. перемен | Ст. откл. зав. перемен | |||
| Сумма кв. остатков | 1, 51e+14 | Ст. ошибка модели |
В данной модели коэффициенты при const, l_length, l_beam являются значимыми на 1% уровне. Уравнение в целом является значимым на 1% уровне и R2 = 0, 668510.
Существенным недостатком данной модели является то, что значительные характеристики модели были исключены при улучшении линейно-логарифмической модели и данная модель характеризует зависимость цены только от размеров судна. Также недостатком является то, что оценки коэффициентов не являются наилучшими в классе несмещенных линейных оценок.
Полученная модель отображает зависимость цены яхты от длины, ширины и осадки судна. В процессе улучшения модели фиктивная переменная region была исключена из модели, но была проинтерпретирована ранее.
Price = -1, 51531e+07 +3, 18289e+06 * ln (length) + 4, 483e+06 * ln (beam) + 453326 ln (draft)
Проинтерпретируем значимые коэффициенты полученной модели:
ü При увеличении длины яхты на 1%, цена увеличивается на 31828.9 евро;
ü При увеличении ширины яхты на 1%, цена яхты увеличивается на 44830 евро;
ü При увеличении осадки яхты на 1%, цена яхты увеличивается на 4533, 26 евро;