Глава 2. Производная. Ее математический и физический смысл. Применение производных для анализа функций и решения практических задач.

ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Определение производной, ее геометрический и механический смысл

Пусть дана функция y = f (x), определенная на множестве D(f). Рассмотрим точку x Î D(f) и некоторое число D x такое, чтобы точка x +D x Î D(f). Это число D x называется приращением аргумента x.

Определение 1. Приращением функции y = f(x) называется разность f (x +D x) - f (x). Приращение функции y = f (x) обозначают D y. То есть D y = f (x +D x) - f (x).

Определение 2. Производной функции y = f(x) называется предел отношения приращения функции D y к приращению аргумента D x, если приращение аргумента D x стремится к нулю и этот предел существует. Производную функции y = f (x) обозначают: 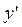или 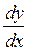. Поэтому можно записать:

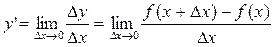
Пример. Исходя из определения, найти производную функции у = .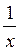

Решение. D y = f (x + D x) - f (x) = = .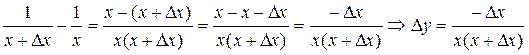

.

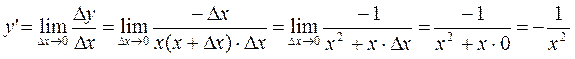Ответ: