Доказательство. 1) необходимость: Дано: y=f(x) дифференцируема в т.х.

1) необходимость: Дано: y = f (x) дифференцируема в т. х.

Доказать: A = f ' (x).

Так как функция y = f (x) дифференцируема в т. х, то по определению

D y = A × D x + a(D x) × D x, где a(D x) ® 0 при D x ®0.

Разделим это равенство на D x # 0:

.

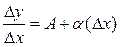Перейдем к пределу при D x ®0:

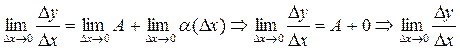существует, а значит f ' (x) = A.

Необходимость доказана.

2) достаточность: Дано: f ' (x) - существует

Доказать: f (x) дифференцируема.

Так как существует f ' (x)= 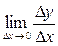, то по свойству предела можно записать:

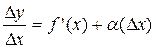, где a(D x)®0 при D x ®0.

Умножим это равенство на D x:

D y = f ' (x) × D x + a(D x) × D x Þ функция y = f (x), дифференцируема в точке х.

Достаточность доказана.

Теорема 2 (связь дифференцируемости с непрерывностью функции).

Если функция y = f (x) дифференцируема в точке x Î D(f), то она непрерывна в этой точке.

Доказательство. Так как функция дифференцируема в точке x, то ее приращение в этой точке можно представить в виде:

D y = A × D x +a(D x) × D x, где A = f ' (x) и a(D x)®0 при D x ®0.

Найдем предел от D y при D x ®0:

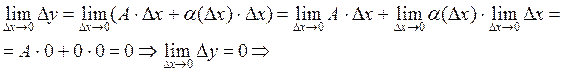
Þ по определению 2 непрерывности функции в точке функция y = f (x) непрерывна в т. x.

Замечание. Обратное теореме 2 утверждение не всегда верно.