Производные показательной и степенной функций

Теорема 7. Степенная функция y = x ^a(aÎ R) дифференцируема при любом x Î R и справедлива формула:

(x ^a)' = a × x ^a-1.

Доказательство. Прологарифмируем равенство y = x ^a, предполагая x > 0:

ln y = a× ln x

Получили уравнение от x и y, задающее функцию y = x ^a неявно. Найдем производные от обеих частей равенства:

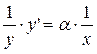
Выразим отсюда y ':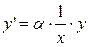

Подставим в полученное равенство y = x ^a:

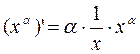
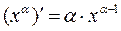
Теорема доказана.

Теорема 8. Показательная функция y = a^x (a > 0, a #1) дифференцируема при любом x Î R и справедлива формула:

(a^x)' = a^x × ln a

Доказательство. Прологарифмируем равенство y = a^x:

ln y = x ln a.

Получили уравнение от x и y, задающее функцию y = a^x неявно. Найдем производные от обеих частей равенства:

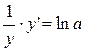
Выразим отсюда y ': y ' = y × ln a.

Подставим в полученное равенство y = a^x :

(a^x)'= a^x × ln a

Теорема доказана.

Замечание. В частном случае, при a = e полученная формула в теореме 8 принимает вид:

(e^x)' = e^x × ln e или (e^x)' = e^x.

Теорема 9. Если функции U (x) и V (x) дифференцируемы в точке x, то показательно-степенная функция y = (U (x)) ^{V ( x )} дифференцируема в точке x и справедлива формула:

((U (x)) ^{V (x)})' = (U (x)) ^{V (x)} × V ' (x) ln U (x) + U ' (x) × V (x) × (U (x)) ^{V (x)-1}.

Доказательство можно выполнить с помощью логарифмирования равенства y =(U (x)) ^{V ( x )} по основанию e и дальнейшего дифференцирования обеих частей полученного равенства.